MATLAB函数随笔画图篇
前言：这些都是我在学习MATLAB与数学建模时遇到的一些常用函数，就在这里写了下。当然MATLAB十分强大，函数众多，这些只是凤毛麟角，这篇博客我也会一直更新有新的函数就接着写上。有不足之处还望指出。
这里是数值计算篇
画图篇
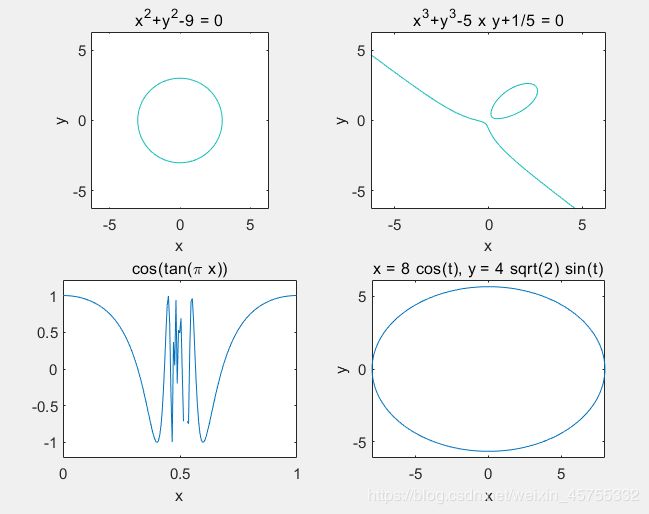
1. 隐函数画图 ezplot
subplot(2,2,1);
ezplot('x^2+y^2-9'); %原式为x^2+y^2-9=0
axis equal %x y轴相等
subplot(2,2,2);
ezplot('x^3+y^3-5*x*y+1/5') % 原式为x^3+y^3-5*x*y+1/5=0
subplot(2,2,3);
ezplot('cos(tan(pi*x))',[ 0,1])
subplot(2,2,4);
ezplot('8*cos(t)','4*sqrt(2)*sin(t)',[0,2*pi])
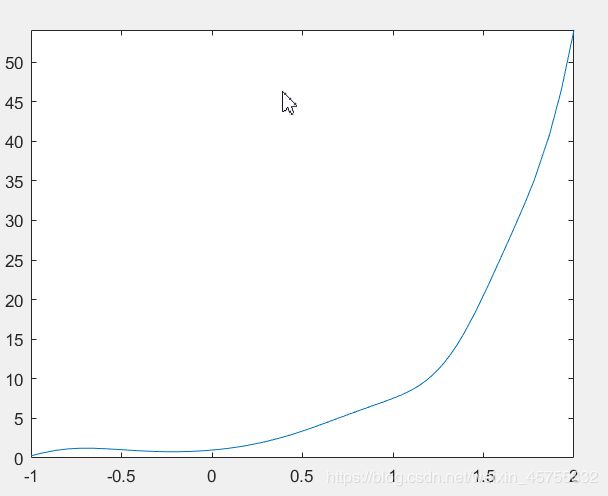
2. fplot(‘fun’,lims)
表示绘制字符串fun指定的函数在lims=[xmin,xmax]的图形.
syms x y
fplot(@(x)exp(2*x)+sin(3*x^2),[-1,2])
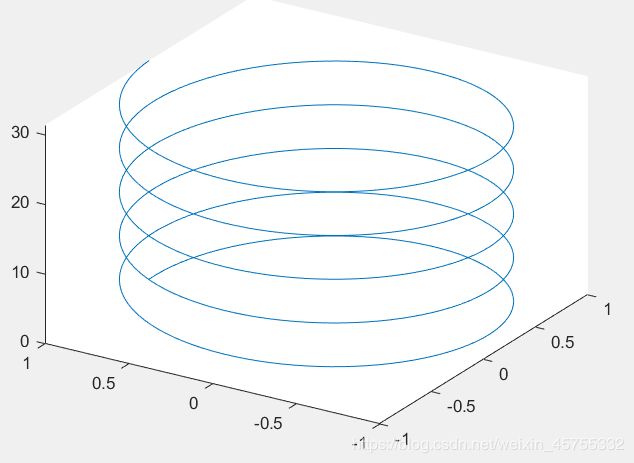
3.空间曲线 plot3
plot3(x,y,z,s)
- 在区间[0，10*pi]画出参数曲线x=sin(t),y=cos(t), z=t.
t=0:pi/50:10*pi;
plot3(sin(t),cos(t),t)
2. 画多条曲线观察函数Z=(X+Y).^2.
x=-3:0.1:3;y=1:0.1:5;
[X,Y]=meshgrid(x,y); % （这里meshgrid(x,y)的作用是产生一个以向量x为行、向量y为列的矩阵）
Z=(X+Y).^2;
plot3(X,Y,Z)
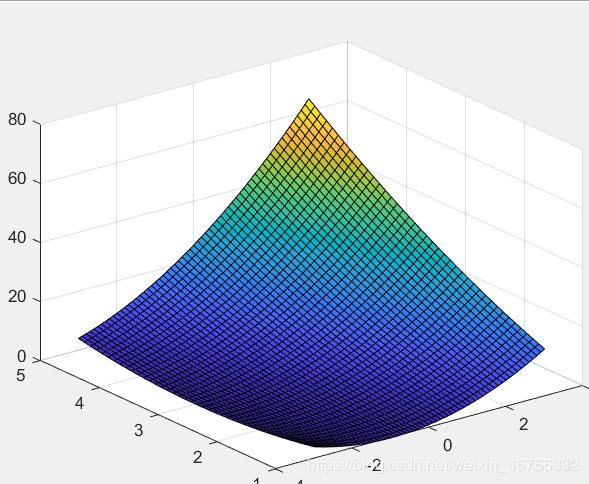
空间曲面 surf
surf(x,y,z)画出数据点（x，y，z）表示的曲面
- 画函数Z=(X+Y).^2的图形
x=-3:0.1:3;y=1:0.1:5;
[X,Y]=meshgrid(x,y);
Z=(X+Y).^2;
surf(X,Y,Z)
mesh(x,y,z) 画网格曲面
- 例 画出曲面Z=(X+Y).^2在不同视角的网格图.
x=-3:0.1:3;y=1:0.1:5;
[X,Y]=meshgrid(x,y);
Z=(X+Y).^2;
mesh(X,Y,Z)
meshz(X,Y,Z) 在网格周围画一个curtain图(如,参考平面)
x=-3:0.1:3;y=1:0.1:5;
[X,Y]=meshgrid(x,y);
Z=(X+Y).^2;
meshz(X,Y,Z)
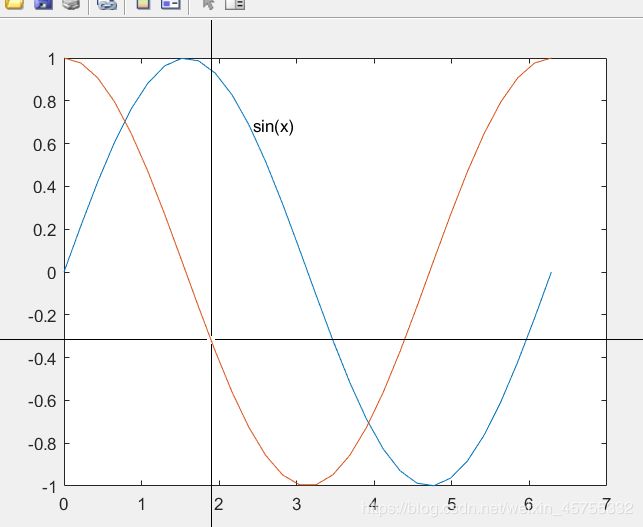
gtext(‘string’)
gtext(‘string’)用鼠标放置标注在现有的图上.运行命令gtext(‘string’)时，屏幕上出现当前图形，在图形上出现一个交叉的十字，该十字随鼠标的移动移动，当按下鼠标左键时，该标注string放在当前十交叉的位置.
x=linspace(0,2*pi,30);
y=sin(x);
z=cos(x);
plot(x,y,x,z)
gtext('sin(x)');
gtext('cos(x)')
定制图形坐标
axis([xmin xmax ymin ymax zmin zmax])
x=linspace(0.0001,0.01,1000);
y=sin(1./x);
plot(x,y)
axis([0.005 0.01 -1 1])
x轴范围是[0.005,0.01]
y轴范围是[-1.1]
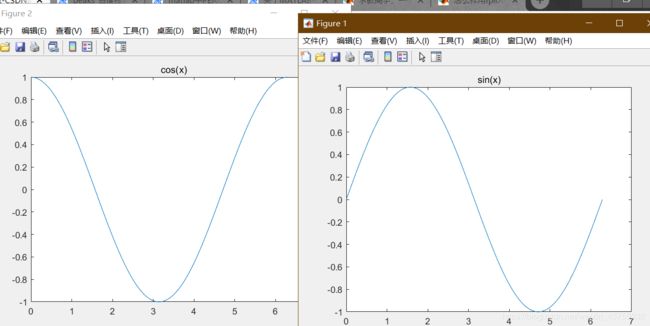
figure(h) 新建h窗口，激活图形使其可见，并把它置于其它图形之上
x=linspace(0,2*pi,100);
y=sin(x);z=cos(x);
plot(x,y);
title('sin(x)');
figure(2);
plot(x,z);
title('cos(x)');
可以看到出现了两个图窗
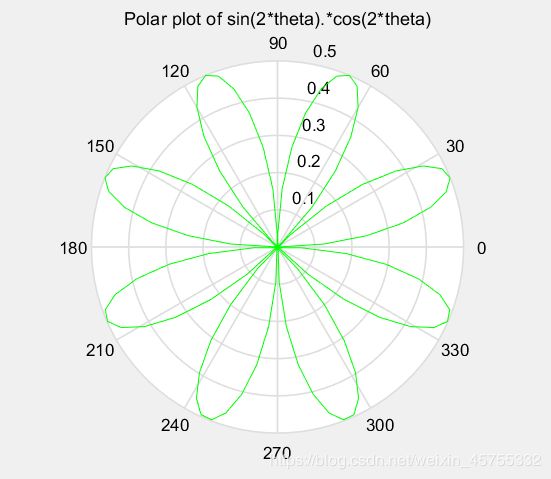
极坐标 polar (theta,rho,s)
用角度theta（弧度表示）和极半径rho作极坐标图，用s指定线型。
theta=linspace(0,2*pi),
rho=sin(2*theta).*cos(2*theta);
polar(theta,rho,'g')
title('Polar plot of sin(2*theta).*cos(2*theta)');
散点图: scatter（X,Y,S,C）
在向量X和Y的指定位置显示彩色圈．X和Y必须大小相同．
grid on或者grid minor添加坐标轴
隐藏坐标轴
x=0:0.1:6;
y=sin(x);
plot(x,y)
set(gca,'ytick',[])
set(gca,'xtick',[])
将多个图形绘制到一个图窗里
在一开始加hold on 就行，不用画一个加一个
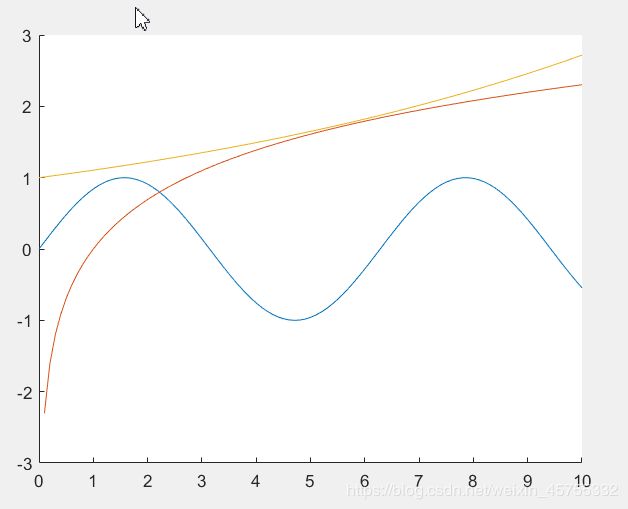
x=0:0.1:10;
hold on
plot(x,sin(x))
plot(x,log(x))
plot(x,exp(x/10))
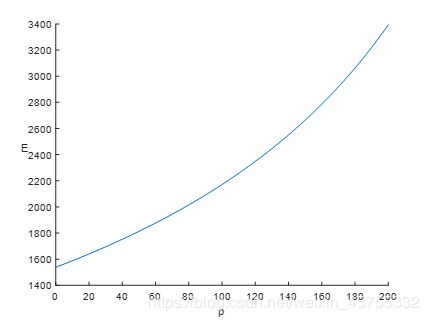
ylabel翻转
原图
plot(x,y)
xlabel('ρ')
set(ylabel('E'),'Rotation',0);
旋转之后
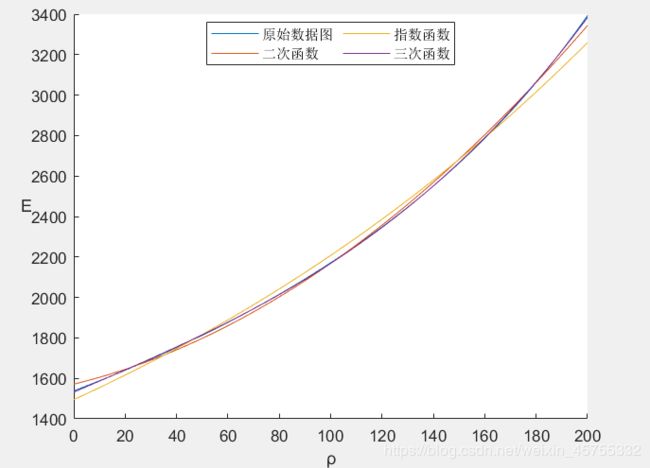
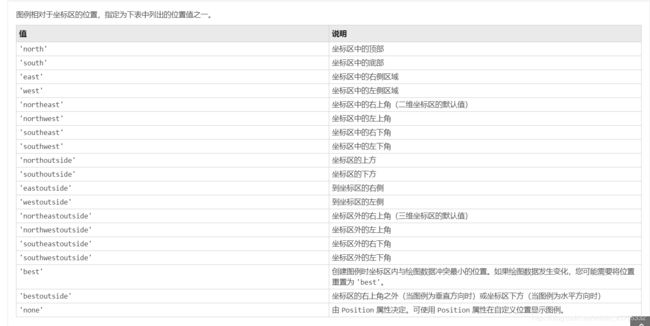
设置legend的位置和显示方式
hold on
x=U3(:,1);y=U3(:,2);
plot(x,y)
xlabel('ρ')
set(ylabel('E'),'Rotation',0);
a=polyfit(x,y,2);
y1=a(3)+a(2)*x+a(1)*x.^2;
plot(x,y1)
b=polyfit(x,log(y),1);
y2=exp(b(2))*exp(b(1)*x);
plot(x,y2)
c=polyfit(x,y,3)
y3=c(4)+c(3)*x+c(2)*x.^2+c(1)*x.^3;
plot(x,y3)
legend('原始数据图','二次函数','指数函数','三次函数','NumColumns',2,'Location','best')
