数学建模之层次分析法及其应用
概述
层次分析法(Analytic Hierarchy Process,简称 AHP)是对一些较为复杂、较为模
糊的问题作出决策的简易方法,它特别适用于那些难于完全定量分析的问题。常用于相互关联、相互制约的众多因素构成的复杂而往往缺少定量数据的系统。
运用层次分析法建模,大体上可按下面四个步骤进行:
- 建立递阶层次结构模型;
- 构造出各层次中的所有判断矩阵;
- 层次单排序及一致性检验;
- 层次总排序及一致性检验
下面将用实例分别阐述这些步骤。
递阶层次结构的建立与特点
我们拿到一个问题,常将其分为若干层次结构,上一层次的元素作为准则对下一层次有关元素起支配作用。
这些层次可以分为三类:.
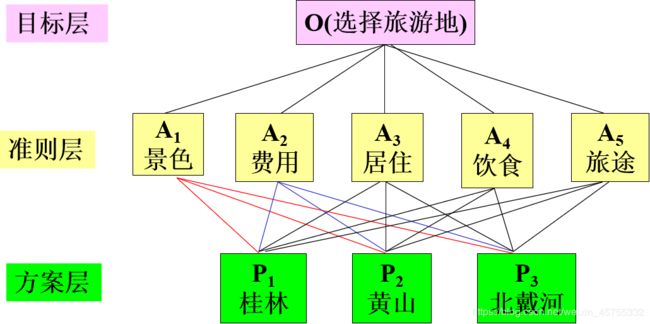
- 最高层:这一层次中只有一个元素,一般它是分析问题的预定目标或理想结果,因此也称为目标层。
- 中间层:这一层次中包含了为实现目标所涉及的中间环节,它可以由若干个层次组成,包括所需考虑的准则、子准则,因此也称为准则层。
- 最底层:这一层次包括了为实现目标可供选择的各种措施、决策方案等,因此也称为措施层或方案层。
递阶层次结构中的层次数与问题的复杂程度及需要分析的详尽程度有关,一般地层次数不受限制。每一层次中各元素所支配的元素一般不要超过 9 个。这是因为支配的元素过多会给两两比较判断带来困难。
构造判断矩阵
构造判断矩阵的方法是一致矩阵法,即:将上述两组权重进行综合,确定各方案对目标的权重。所有元素之间采用相对尺度两两对比,确定权重。
| 标度 | 含 义 |
|---|---|
| 1 | 表示两个因素相比,具有相同重要性 |
| 3 | 表示两个因素相比,前者比后者稍重要 |
| 5 | 表示两个因素相比,前者比后者明显重要 |
| 7 | 表示两个因素相比,前者比后者强烈重要 |
| 9 | 表示两个因素相比,前者比后者极端重要 |
| 2,4,6,8 | 表示上述相邻判断的中间值 |
| 倒数 | 若因素i 与因素 j 的重要性之比为 a i j a_{ij} aij ,那么因素 j 与因素i 重要性之比为 a i j = 1 / a i j a_{ij}= 1/a_{ij} aij=1/aij |
确定A1-A5的权重,如A1相对A4来说,A1比A4稍微重要,所以矩阵Z(1,4)=3.其对称位置就是1/3。
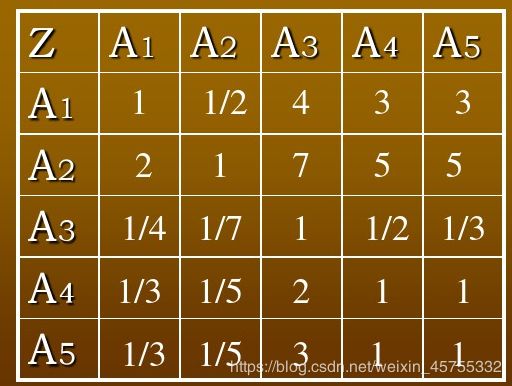
注:Z是成对比较、正互反矩阵。
层次单排序及一致性检验
所谓层次单排序是指根据判断矩阵计算对于上一层某因素而言本层次与之有联系的因素的重要性次序的权值。它是本层次所有因素相对上一层而言的重要性进行排序的基础。

满足 a i j ∗ a j k = a i k a_{ij}*a_{jk}= a_{ik} aij∗ajk=aik的正互反矩阵称为一致矩阵
定理 1:
正互反矩阵 A 的最大特征根 λ m a x λ_{max} λmax必为正实数,其对应特征向量的所有分量均为正实数。 A 的其余特征值的模均严格小于 λ m a x λ_{max} λmax。
定理 2
若 A 为一致矩阵,则
- A 必为正互反矩阵。
- A 的转置矩阵 A T A^T AT也是一致矩阵。
- A 的任意两行成比例,比例因子大于零,从而 rank(A) = 1(同样, A 的任意两列也成比例)。
- A 的最大特征值 λ m a x λ_{max} λmax = n ,其中n 为矩阵 A 的阶。A 的其余特征根均为零。
- 若 A 的最大特征值 λ m a x λ_{max} λmax 对应的特征向量为 W = ( w 1 . . . w n ) T W={(w_1 ... w_n)}^T W=(w1...wn)T ,则 s i j = w i w j s_{ij}=\frac{w_i}{w_j} sij=wjwi

定理 3
n 阶正互反矩阵 A 为一致矩阵当且仅当其最大特征根 λ m a x = n λ_{max} = n λmax=n ,且当正互反矩阵 A 非一致时,必有 λ m a x > n λ_{max}> n λmax>n 。
根据定理 3,我们可以由 λ m a x λ_{max} λmax 是否等于n 来检验判断矩阵 A 是否为一致矩阵。
对判断矩阵的一致性检验的步骤如下:
- 计算一致性指标 C I = λ m a x − n n − 1 CI=\frac{λ_{max}-n}{n-1} CI=n−1λmax−n
- 查找相应的平均随机一致性指标 RI 。对n = 1 …9,Saaty 给出了 RI 的值,如表 2 所示。

计算一致性比例 C R = C I R I CR=\frac{CI}{RI} CR=RICI
当 C R < 0.10 CR < 0.10 CR<0.10时,认为判断矩阵的一致性是可以接受的,否则应对判断矩阵作适当修正。
层次总排序及一致性检验
上面我们得到的是一组元素对其上一层中某元素的权重向量。我们最终要得到各元素,特别是最低层中各方案对于目标的排序权重,从而进行方案选择。总排序权重要自上而下地将单准则下的权重进行合成。



对层次总排序也需作一致性检验,检验仍象层次总排序那样由高层到低层逐层进行。这是因为虽然各层次均已经过层次单排序的一致性检验,各成对比较判断矩阵都已具有较为满意的一致性。但当综合考察时,各层次的非一致性仍有可能积累起来,引起最终分析结果较严重的非一致性。
设 B 层中与 Aj 相关的因素的成对比较判断矩阵在单排序中经一致性检验,求得单排序一致性指标为CI( j) ,( j = 1,L,m ),相应的平均随机一致性指标为 RI( j) (CI( j)、RI( j) 已在层次单排序时求得),则 B 层总排序随机一致性比例为

层次分析法的应用
在应用层次分析法研究问题时,遇到的主要困难有两个:
- 如何根据实际情况抽象出较为贴切的层次结构;
- 如何将某些定性的量作比较接近实际定量化处理。
层次分析法对人们的思维过程进行了加工整理,提出了一套系统分析问题的方法,为科学管理和决策提供了较有说服力的依据。但层次分析法也有其局限性,主要表现在:
3. 它在很大程度上依赖于人们的经验,主观因素的影响很大,它至多只能排除思维过程中的严重非一致性,却无法排除决策者个人可能存在的严重片面性。
4. 比较、判断过程较为粗糙,不能用于精度要求较高的决策问题。AHP 至多只能算是一种半定量(或定性与定量结合)的方法。

回顾总结
例题
挑选合适的工作。经双方恳谈,已有三个单位表示愿意录用某毕业生。该生根据已有信息建立了一个层次结构模型,如图所示
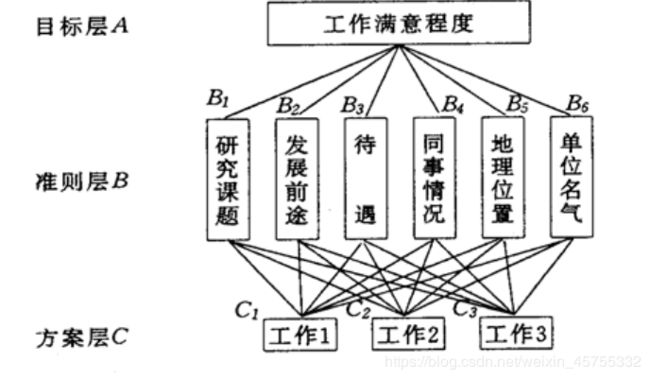
标准层的判断矩阵也已给出
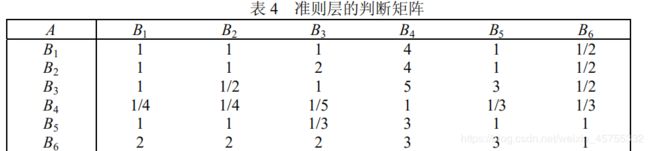
方案层的判断矩阵给出
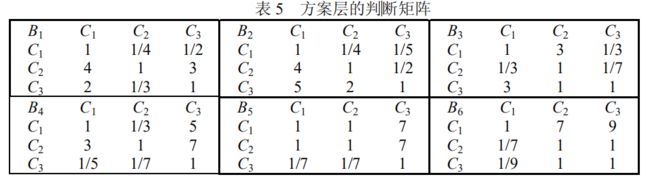
函数文件:
function [CR,quan]=AHPfun(A)
n=size(A,1);
[V,D] = eig(A); %V 是特征向量,D是由特征值构成的对角矩阵(除了对角线元素外,其余位置元素全为0)
Max_eig = max(D(:)); %那么怎么找到最大特征值所在的位置了?需要用到find函数,它可以用来返回向址或者矩阵中不为0的元素的位置索引。
%那么问题来了,我们要得到最大特征值的位置,就需婴将包含所有特征值的这个对角矩阵D中,不等于最大特征值的位置全变为
%这时候可以用到矩阵与常数的大小判断运算
D = Max_eig;
[r,c]=find(D == Max_eig,1);
%找到D中第“个与最大特征值相等的元素的位置,记录它的行和列。
%第二步:对求出的特征向量进行归-“化即可得到我们的权重
quan=V(:,c)./sum(V(:,c));
%我们先根据上面找到的最大特征值的列数c找到对应的特征向量,然后再进行标准化。
% 计算一致性比例CR
CI = (Max_eig - n)/(n-1);
RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59]; %注意哦,这里的RI最多支持n = 15
CR=CI/RI(n);
end
主文件:
clc;clear
a0=[1 1 1 4 1 1/2
1 1 2 4 1 1/2
1 1/2 1 5 3 1/2
1/4 1/4 1/5 1 1/3 1/3
1 1 1/3 3 1 1
2 2 2 3 3 1 ];
a1=[1 1/4 1/2;
4 1 3;
2 1/3 1 ];
a2=[1 1/4 1/5;
4 1 1/2;
5 2 1 ];
a3=[1 3 1/3;
1/3 1 1/7;
3 7 1 ];
a4=[1 1/3 5;
3 1 7;
1/5 1/7 1];
a5=[1 1 7;
1 1 7;
1/7 1/7 1 ];
a6=[1 7 9;
1/7 1 1;
1/9 1 1];
F=cat(3,a1,a2,a3,a4,a5,a6);
[a,b,c]=size(F);
all=ones(3,c);
cr=[];
[CR,quan]=AHPfun(a0);
cr0=CR;
quan0=quan;
disp('准则层权值为:');disp(quan0');
disp('准则层一致性比例为:');disp(cr0);
for i =1:c
A=F(:,:,i);
[CR,quan]=AHPfun(A);
cr=[cr,CR];
all(:,i)=quan;
end
allquan=ones(3,1);
for j=1:3
allquan(j,1)=sum(all(j,:).*quan0');
end
disp('方案层单排序权值:');disp(all);
disp('方案层一致性比例为:');disp(cr);
disp('总排序权值:');disp(allquan);
输出:
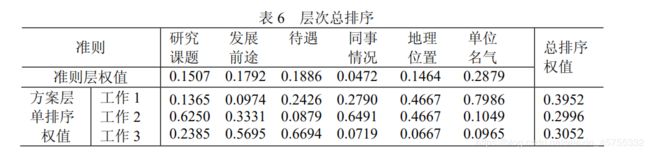
准则层权值为:
0.1507 0.1792 0.1886 0.0472 0.1464 0.2879
准则层一致性比例为:
0.0981
方案层单排序权值:
0.1365 0.0974 0.2426 0.2790 0.4667 0.7986
0.6250 0.3331 0.0879 0.6491 0.4667 0.1049
0.2385 0.5695 0.6694 0.0719 0.0667 0.0965
方案层一致性比例为:
0.0176 0.0236 0.0068 0.0624 -0.0000 0.0068
总排序权值:
0.3952
0.2996
0.3052