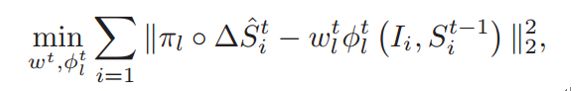Face Alignment at 3000 FPS via Regressing Local Binary Features 阅读笔记
基于局部二值特征的人脸形状回归
FaceAlignment at 3000 FPS via Regressing Local Binary Features阅读笔记
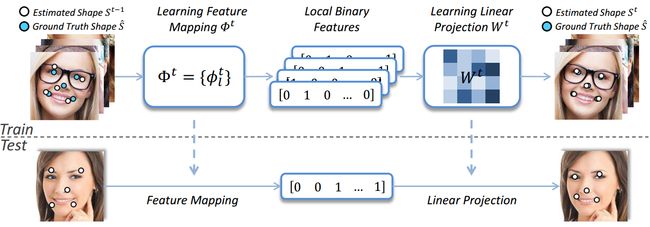
该篇文章与CVPR2012年的ESR相比,亮点在于:1)提取一系列局部二值特征(LBF);2)采用局部性原理对这些特征进行学习。整体思路:1)采用随机森林训练学习获得LBF;2)使用全局线性回归训练获取线性矩阵求得形状残差。
一、形状回归介绍
在介绍形状回归之前,先来了解几个名词:形状,相对形状,绝对形状。
形状指的是所有关键点的集合;形状可以分为两种:一种是绝对形状,关键点的位置是相对于整幅图像而言,取值在(0-width,0-height);另一种是相对形状,关键点的位置是相对于人脸框,取值在(0-1,0-1),两种形状可以通过人脸框进行相互转换。
形状回归通过级联形式对脸部形状S进行预测,设定初始形状 ![]() ,通过每个级联阶段获得的形状增量
,通过每个级联阶段获得的形状增量 ![]() ,逐步地对形状S进行更新,在第t个阶段,形状增量可以用如下表达式进行表示:
,逐步地对形状S进行更新,在第t个阶段,形状增量可以用如下表达式进行表示:
其中:I表示输入图像, ![]() 为前一阶段形状,
为前一阶段形状, ![]() 为特征映射函数,
为特征映射函数,![]() 为线性回归矩阵。这里
为线性回归矩阵。这里 ![]() 只取决于I和
只取决于I和 ![]() 。第t阶段的形状
。第t阶段的形状 ![]() 。
。
二、该篇文章创新点:采用局部性原理提取学习特征
采用局部性原理学习特征主要考虑两点:1)实际问题:采用整个人脸区域作为训练输入导致特征池过大,不仅导致训练的开销增大,而且无法提取比较有判别力的特征;2)泛化能力:特征池过大导致噪声增多,很容易造成过拟合现象。特征提取方法:由于最具有判别力的纹理信息是分布在上一阶段的特征点的附近区域,因此,在每一个阶段对特征提取时,只在上一阶段的特定的特征点附近半径r的区域提取。
三、 Regressing Local Binary Features
实现主要步骤
Step1:为每一个特征点学习出一个特征映射函数![]() ,将所有 组合可得
,将所有 组合可得![]() ;
;
Step2:通过线性回归,获得![]() 。通过级联的方式,一遍又一遍的重复性学习获得。
。通过级联的方式,一遍又一遍的重复性学习获得。
论文方法整体过程:
训练阶段:
1)学习特征映射函数 ![]() 生成局部二值特征LBF;
生成局部二值特征LBF;
2)根据LBF特征和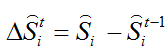 训练获得线性回归矩阵
训练获得线性回归矩阵![]() ,
, ![]() 表示标注形状;
表示标注形状;
测试阶段:
1)利用学习的特征映射函数![]() 生成 LBF特征+训练学习得到的
生成 LBF特征+训练学习得到的 ![]() 获得形状增量
获得形状增量![]()
3)更新形状;
3.1. Learning local binary features
(1)![]() 是由一系列独立的局部二值特征映射函数组成。
是由一系列独立的局部二值特征映射函数组成。
(2)每一![]() 可独立地在相应特征点第l个特征点附近区域通过回归获得。
可独立地在相应特征点第l个特征点附近区域通过回归获得。
(3)通过这种方法可以筛选出大量的噪声,减少学习的复杂性从而获得较好的回归效果。
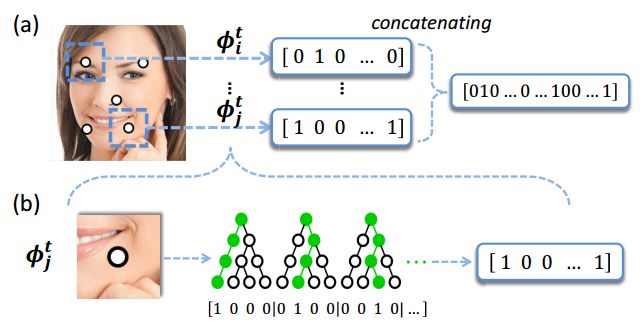
为了学习![]() 和预测特征点位置,文章只在局部区域使用基于回归的集成树生成二值特征,然后将二值特征进行组合获得局部二值特征。集成树使用的是随机森林。
和预测特征点位置,文章只在局部区域使用基于回归的集成树生成二值特征,然后将二值特征进行组合获得局部二值特征。集成树使用的是随机森林。
图二.LBF特征提取过程
最佳区域大小
局部二值特征 ![]() 学习通过对每个特征点在对应的局部区域上学习,使用决策树索引二值特征,所谓决策树是一种由上而下的学习过程,在每个节点的决策阶段,会根据阈值等判断条件分裂成多个事件,直到分裂到叶节点为止。局部二值特征的定位方法使用两点像素的差值和阀值判断索引特征的分裂,将每个特征点的特征空间分裂成和叶节点相同数目的类别,每个类别对应的二进制位用0或1二进制表示。
学习通过对每个特征点在对应的局部区域上学习,使用决策树索引二值特征,所谓决策树是一种由上而下的学习过程,在每个节点的决策阶段,会根据阈值等判断条件分裂成多个事件,直到分裂到叶节点为止。局部二值特征的定位方法使用两点像素的差值和阀值判断索引特征的分裂,将每个特征点的特征空间分裂成和叶节点相同数目的类别,每个类别对应的二进制位用0或1二进制表示。
随机树是如何训练?
训练目标函数:
当i遍历所有训练样本, ![]() 从
从![]() 中随机抽取两个元素
中随机抽取两个元素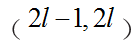 ,
,![]() 表示第i和训练样本在第l 个特征点上的偏差。从目标函数看来,在对随机森林进行训练完后,不仅可以获得
表示第i和训练样本在第l 个特征点上的偏差。从目标函数看来,在对随机森林进行训练完后,不仅可以获得 ![]() ,还可以获得
,还可以获得![]() ,那为啥还需要去学习
,那为啥还需要去学习 ![]() ?
?
3.2. Learning global linear regression![]()
由于通过对随机森林学习得到的 ![]() 只是针对某个局部特征点而言,而非整个形状。文章中摒弃使用局部回归矩阵
只是针对某个局部特征点而言,而非整个形状。文章中摒弃使用局部回归矩阵![]() ,而是进行全局线性回归。
,而是进行全局线性回归。
在对随机森林进行训练之后,可以获得LBF特征,而根据当前形状与groundTrue形状进行比较,可以获得形状增量 ![]() ,根据公式
,根据公式![]() 进行训练可以求得
进行训练可以求得![]() ;
;
在由于LBF是高度稀疏,因此,在文章中使用双坐标下降法求解高度稀疏线性模型,双坐标下降法可以使用liblinear库。(libsvm库,liblinear库)
这里第一项是回归的目标,第二项是 ![]() 的L2范数的正则化,
的L2范数的正则化, ![]() 控制正则化的强度,也就是惩罚因子。
控制正则化的强度,也就是惩罚因子。
为啥需要进行正则化?
假设是对68个特征点进行训练,那么 ![]() 维度可达100K+,过多的特征在学习过程中会极容易出现过拟合情况。
维度可达100K+,过多的特征在学习过程中会极容易出现过拟合情况。
避免过拟合问题有两种方法:
方法一:尽量减少选取变量的个数。
不过这就意味着舍弃部分特征变量。那么哪些是需要舍弃的,哪些是不能舍弃的?而且如果每一个变量都对结果存在影响的话,该咋办?
方法二:正则化。正则化中将保留所有的特征变量,但是会减小特征变量的数量级。http://www.cnblogs.com/jianxinzhou/p/4083921.html
该链接有详细介绍了正则化。
文章的主要内容就以上这些。
讨论:
1)随机森林中的决策树节点的分裂依赖于索引特征和分裂的阈值。
2)在学习局部二值特征映射时,随机森林的深度不容易控制,很容易受到不同训练集的影响,当问题比较复杂时,树的深度会变得很深,很容易造成过拟合,以及导致占用内存空间过大,缺少剪枝。
3)在随机森林的回归中,叶子节点保存的是所有分到该叶节点的形状误差和的平均值,训练的目标损失函数是保证所有树的平均误差最小。为了和测试误差保持一致,理想的损失函数应该是对所有树叶子节点形状求平均,然后在计算误差损失,训练和测试损失函数的不一致性,导致目标优化是一个次优问题。