动手学深度学习 Task1笔记-线性回归
# 线性回归;Softmax与分类模型、多层感知机
参加datawhale与伯禹学习平台及K-Lab合作的《动手学深度学习》的Pytorch版本。
2.11-2.14
一、线性回归
线性模型
假设价格只取决于房屋状况的两个因素,即面积(平方米)和房龄(年)。探索价格与这两个因素的具体关系。线性回归假设输出与各个输入之间是线性关系:
![]()
损失函数
在模型训练中,需要衡量价格预测值与真实值之间的误差。通常选取一个非负数作为误差,且数值越小表示误差越小。一个常用的选择是平方函数。 样本误差i的表达式为:
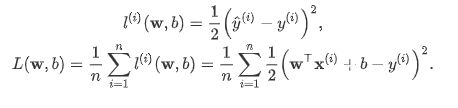
优化函数 - 随机梯度下降-SGD
在求数值解的优化算法中,小批量随机梯度下降(mini-batch stochastic gradient descent)在深度学习中被广泛使用。
其算法为:
1.先选取一组模型参数的初始值(如随机选取);
2.对参数进行多次迭代,使每次迭代都可能降低损失函数的值:
2.1.在每次迭代中,随机均匀采样一个由固定数目训练数据样本所组成的小批量(mini-batch)B;
2.2.求小批量中数据样本的平均损失有关模型参数的导数(梯度);
2.3.用此结果与预先设定的一个正数的乘积作为模型参数在本次迭代的减小量。

矢量计算
在模型训练或预测时,常同时处理多个数据样本并用到矢量计算。在介绍线性回归的矢量计算表达式之前,让我们先考虑对两个向量相加的两种方法。
1.向量相加的一种方法是,将这两个向量按元素逐一做标量加法。
2.向量相加的另一种方法是,将这两个向量直接做矢量加法。
线性回归模型使用Pytorch的简洁实现
生成数据集
读取数据集
定义模型
初始化模型参数
定义损失函数
定义优化函数
训练
二、Softmax与分类模型
softmax的基本概念
单层神经网络

softmax运算符

交叉熵损失函数



softmax的简洁实现
初始化参数和获取数据
定义网络模型
初始化模型参数
定义损失函数
定义优化函数
训练
三、多层感知机
表达公式

激活函数
1.ReLU函数:只保留正数元素,并将负数元素清零。
![]()
函数图像:

2.Sigmoid函数:
可以将元素的值变换到0和1之间:
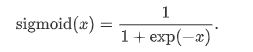
函数图像:

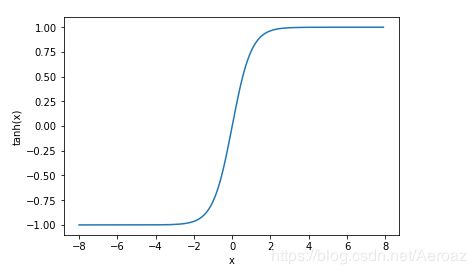
3.tanh函数:
tanh(双曲正切)函数可以将元素的值变换到-1和1之间:
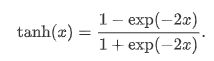
函数图像:
关于激活函数的选择
ReLu函数是一个通用的激活函数,目前在大多数情况下使用。但是,ReLU函数只能在隐藏层中使用。
用于分类器时,sigmoid函数及其组合通常效果更好。由于梯度消失问题,有时要避免使用sigmoid和tanh函数。
在神经网络层数较多的时候,最好使用ReLu函数,ReLu函数比较简单计算量少,而sigmoid和tanh函数计算量大很多。
在选择激活函数的时候可以先选用ReLu函数如果效果不理想可以尝试其他激活函数。
#多层感知机pytorch实现
import torch
from torch import nn
from torch.nn import init
import numpy as np
import sys
sys.path.append("/home/kesci/input")
import d2lzh1981 as d2l
print(torch.version)
#初始化模型和各个参数
num_inputs, num_outputs, num_hiddens = 784, 10, 256
net = nn.Sequential(
d2l.FlattenLayer(),
nn.Linear(num_inputs, num_hiddens),
nn.ReLU(),
nn.Linear(num_hiddens, num_outputs),
)
for params in net.parameters():
init.normal_(params, mean=0, std=0.01)
#训练
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size,root=’/home/kesci/input/FashionMNIST2065’)
loss = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(net.parameters(), lr=0.5)
num_epochs = 5
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, None, None, optimizer)