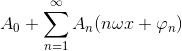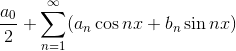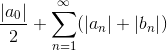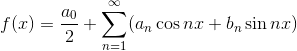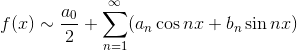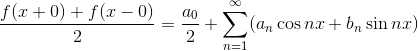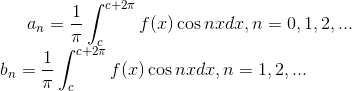Galois_Mar
Galois_Mar

傅里叶级数

三角级数·正交函数系

最简单的周期运动,可用正弦函数

                                                                       y=A\sin (\omega x+\varphi ) (1)

来描述,由(1)所表达的周期运动也称为简谐振动.由无穷多个简谐振动进行叠加就得到函数项级数

                                                                     A_0+\sum_{n=1}^{\infty }A_n\siin (n\omega x+\varphi _n)(2).

若级数(2)收敛,则它所描述的是更为一般的周期运动现象.只讨论\omega=1的情形得

                                                                 \frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\cos nx+b_n\sin nx)(3).

它是由三角函数列(也称三角函数系)

                                                 1,\cos x , \sin x,\cos 2x, \sin 2x,...\cos nx,\sin nx,... (4)

所产生的一般形式的三角级数.其中记A_0=\frac{a_0}{2},A_n\sin \varphi _n=a_n,A_n\cos \varphi_n=b_n,n=1,2,3,....

 

若两个函数\varphi与\psi在[a,b]上可积,且\int_{a}^{b}\varphi (x)\psi (x)dx=0,则称函数\varphi与\psi在[a,b]上是正交的.由此,三角函数系(4)在[-\pi,\pi]上具有正交性,或称(4)是正交函数系.

一致收敛判别定理

若级数\frac{\left | a_0 \right |}{2}+\sum_{n=1}^{\infty }(\left | a_n \right |+\left | b_n \right |)收敛,则级数(4)在整个数轴上绝对收敛且一致收敛.

在三角函数系(4)中,任何两个不相同的函数的乘积在[-\pi,\pi]上的积都等于零,即

                                                                \int_{-\pi }^{\pi }\cos nxdx=\int_{-\pi }^{\pi }\sin nxdx=0,

                                                                 \int_{-\pi }^{\pi }\cos mx\cos nxdx=0(m \neq n),

                                                                \int_{-\pi }^{\pi }\sin mx\sin nxdx=0(m \neq n),

                                                                 \int_{-\pi }^{\pi }\cos mx\sin nxdx=0.

在三角函数系(4)中任何一个函数的平方在[-\pi,\pi]上的积分都不等于零,即

                                                                 \int_{-\pi }^{\pi }\cos ^{2}nxdx=\int_{-\pi }^{\pi }\sin ^{2}nxdx=\pi ,

                                                                 \int_{-\pi }^{\pi }1^{2}dx=2\pi .

棣莫弗公式                                               (\cos \theta +i\sin \theta)^{n}=\cos n\theta +i\sin n\theta .

以2 \pi为周期的傅里叶级数

若在整个数轴上

                                                                f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\cos nx+b_n\sin nx)(5)

且等式右边级数一致收敛,则有如下关系式：

                                                              a_n=\frac{1}{\pi}\int_{-\pi }^{\pi }f(x)\cos nxdx , n=0,1,2,...(6a)

                                                              b_n=\frac{1}{\pi}\int_{-\pi }^{\pi }f(x)\sin nxdx , n=1,2,...(6b)

一般地说,若f是以2 \pi为周期且在[-\pi,\pi]上可积的函数,则a_n,b_n称为函数f(关于三角函数系)的傅里叶系数,三角级数(5)称为f(关于三角函数系)的傅里叶级数,记作

                                                               f(x)\sim \frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\cos nx+b_n\sin nx)(7)

上式中,符号"~"仅表示三角级数是由f(x)所生成的,并不意味着级数就等于f(x)也不意味着级数是否收敛. 

傅里叶级数收敛定理

以2 \pi为周期的函数f在[-\pi,\pi]上按段光滑，则在每一点x\in [-\pi ,\pi],f的傅里叶级数(7)收敛于f在点x的左、右极限的算术平均值,即

                                                             \frac{f(x+0)+f(x-0)}{2}=\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\cos nx+b_n\sin nx)

其中a_0,b_0为f的傅里叶系数.

下面先对定理中的某些概念作解释,然后举例说明如何运用这个定理把函数展开成傅里叶级数.

我们知道,若f的导函数在[a,b]上光滑.但若定义在[a,b]上除了至多有有限个第一类间断点的函数f的导函数在[a,b]上除了至多有限个点外都存在且连续,且在这有限个点上导函数f'的左、右极限存在,则称f在[a,b]上按段光滑.

根据上述定义,若函数f在[a,b]上按段光滑,则有如下重要性质：

1.f在[a,b]上可积.

2.在[a,b]上每一点都存在f(x\pm 0),且有

                                                               \lim_{t\to 0^{+}}\frac{f(x+t)-f(x-0)}{t}=f'(x+0),

                                                               \lim_{t\to 0^{+}}\frac{f(x-t)-f(x-0)}{-t}=f'(x-0).

3.补充定义f'在[a,b]上那些至多有限个不存在点上的值后(仍记为f'),f'在[a,b]上可积.

从几何图形上讲,在区间[a,b]上按段光滑函数,是由有限个光滑弧段所组成,它至多有有限个第一类间断点和角点.

推论  若f是以2 \pi为周期的连续函数,且在[-\pi,\pi]上按段光滑,则f的傅里叶级数在(-\infty ,+\infty )上收敛于f.

根据收敛定理的假设,f是以2 \pi为周期的函数,所以系数公式(6)中的积分区间[-\pi,\pi]可以改为长度为2 \pi的任何区间,而不影响a_n,b_n的值：

                                                             a_n=\frac{1}{\pi}\int_{c}^{c+2\pi }f(x)\cos nxdx , n=0,1,2,...\\ b_n=\frac{1}{\pi}\int_{c }^{c+2\pi}f(x)\cos nxdx , n=1,2,...(6')

其中c为任何实数.

注意：在具体讨论函数的傅里叶级数展开式时,常只给出函数f在(-\pi,\pi](或[-\pi,\pi))上的表达式,但应理解为它是定义在整个数轴上以2 \pi为周期的函数.即在(-\pi,\pi]以外的部分按函数在(-\pi,\pi]上的对应关系作周期延拓.如f为(-\pi,\pi]上的解析表达式,那么周期延拓后的函数为

                                                               \hat{f}(x)=\left\{\begin{matrix} f(x),x\in (-\pi ,\pi],\\ f(x-2k\pi),x\in ((2k-1)\pi ,(2k+1)\pi ],k=\pm 1,\pm 2,...\end{matirx}\right

因此我们说函数f的傅里叶级数就是指函数\hat{f}的傅里叶级数.

 

 

 

 

你可能感兴趣的:(数学分析)

  • 也是幸福啊 媚阳_晞
    套用一句脍炙人口的话“世上没有不散的宴席”。坐在窗边，炎热的夏天也有清爽的凉风，手边的数学分析课本，与未合上盖儿的签字笔，暗示着我还年轻。窗下的他们，松垮垮的黑色大衣，看起来似乎是油性防水的，不知道摸起来怎么样，V形领却美丽地五彩缤纷，粉色、黄色使整体看起来不算太暗沉。再过一年，我希望在这件衣服里，我搭配的是不太长的头发，也不至于太短，可能画个淡妆，最好别因为流汗而狼狈，我是极意流汗的，嗯，内里应
  • csp-j2022-2023解析 lcxz 算法c++开发语言
    P9748[CSP-J2023]小苹果这个问题可以通过数学分析来解决。我们需要找到一个规律，描述每天拿走的苹果编号以及最终拿走所有苹果所需的天数。首先，我们注意到小苞每天拿走的苹果编号形成了一个等差数列，公差为2。第一天拿走的苹果编号为1,3,5,...,n−11,3,5,...,n-11,3,5,...,n−1（如果n是偶数），或者1,3,5,…(如果n是奇数)。我们可以发现，每天拿走的苹果数量
  • 【大模型实战篇】大模型周边NLP技术回顾及预训练模型数据预处理过程解析（预告） 源泉的小广场 大模型自然语言处理人工智能大模型LLM预训练模型数据预处理高质量数据
    1.背景介绍进入到大模型时代，似乎宣告了与过去自然语言处理技术的结束，但其实这两者并不矛盾。大模型时代，原有的自然语言处理技术，依然可以在大模型的诸多场景中应用，特别是对数据的预处理阶段。本篇主要关注TextCNN、FastText和Word2Vec等低成本的自然语言处理技术，如何在大模型时代发挥其余热。今天先抛出这个主题预告，接下来会花些时间，逐步细化分析这些周边技术的算法原理、数学分析以及大模
  • 高中数学（从函数极限到积分） 小杨洲
    数学分析极限与导数1.数列和函数极限数列极限定义。设{xn}为一个数列，若∃a为常数，对于∀ε>0，总有∃N∈N*，使得当n>N时，不等式|xn-a|n}的极限（数列收敛于a）。数列极限记为limn→∞xn=a，若不存在常数a说明该数列无极限或发散，表示limn→∞xn不存在。收敛极限得性质有唯一性（极限值），有界性（收敛则有界），保号性（数列xn≤yn，则对应极限a≤b），四则运算（加减乘除），
  • 数学分析视频+书籍等 dllglvzhenfeng 计算机考研机试创新程序猿的数学人工智能算法信奥青少年趣味编程数学分析
    数学分析（数学基础分支）数学分析（数学基础分支）_百度百科《数学分析（一）》专题《数学分析（一）》专题_哔哩哔哩_bilibili北京某高校《数学分析（二）》：第一讲~第五讲北京某高校《数学分析（二）》：第一讲~第五讲_哔哩哔哩_bilibili北京某高校《数学分析（二）》：第六讲~第八讲（未完待续）北京某高校《数学分析（二）》：第六讲~第八讲_哔哩哔哩_bilibili北京某高校《微观数学》之《
  • ns3学习之初识ns3 特立独行的一只miao ns3学习ns3学习
    由于网络的不可控性、易变和不可预测等特性，给新的网络方案的验证、分析和比较带来的极大的困难。NS3是一个离散事件模拟器，旨在满足学术研究和教学的需求。NS3项目是一个始于2006年的开源项目，负责开发ns3软件。NS-3并不是NS-2的扩展，而是一个全新的模拟器。网络通信研究方法：分析方法：在理论和协议层面上对网络通信技术或系统进行研究分析，抽象出数学分析模型，利用数学分析模型对问题进行求解。如采
  • 憨逼的考研日记（一） 星空_59e5
    慢慢的，活成了自己最讨厌的样子（序言，本人今年大四毕业，三月份到八月份一直在小城单位工作，工资在平均7000左右。九月份回学校二战，金融跨考数学，目标某985。复习进度，数学分析复习到最后两章节，高等代数基础复习到第六章，共十章。政治英语没复习，还有十四天考试，去年凉，今年凉凉！）武汉的冬天真的有点冷，早上六点多脚蹬了一下墙，墙上留下了一个洞，我自己也醒了，瞄了一眼落地窗，漆黑黑的，等天亮了，在起
  • 范畴论系列（一）初识范畴 数学
    起因写这个系列起源于自己学习编程语言时遇到的问题，研究编程语言不可避免要与数学打交道，自己大学只学过数学分析和高等代数等数学系一年级课程，PLT(ProgrammingLanguageTheroy)需要的数学基础大致为：抽象代数（AbstractAlgebra）、拓扑（Topology）、范畴（CategoryTheory）等代数知识，在阅读相关PL书籍时，深感自己的无力。我又是一个"死磕"的人，
  • 数学学习，研究和一些思想 醉里且歌花漫天
    数学学习当中有一些基础知识，思想，方法和手段，一些常见的处理技巧，一些结论，要做的题目，题库和一系列的东西。一些基础知识，定理，结论和题目，以及其中的思想。第六章微分中值定理及其应用数学要多分析，多总结。数学教材的逻辑：定义->性质->证明->应用，做题->题目->不同章节的题目可能要放在一起处理。一些特殊的结论，要处理的东西，学习数学中记忆力是很关键的东西数学分析常用方法数学学习要解决的几个问题
  • 概率论与数理统计——二、随机变量及其分布 米妮爱分享
    1随机变量随机变量是把样本S映射到R(实值单值)函数随机变量的引入可以来描述各种随机现象，并能利用数学分析的方法对随机实验的结果进行深入广泛的研究和讨论。2离散随机变量及其分布律（一）（0-1）分布（二）伯努力试验、二项分布（三）泊松分布3随机变量的分布函数计算分布函数时，根据其分布律，计算某一范围的概率时，左边x是小于不等于x的，当等于时，拆开的等式在3.1中还需要加上等于此值的概率，见例子。4
  • 大学数学分析题库搜题软件？多功能全科目的大学搜题神器 #其他#学习方法#学习方法 雷霆嘎巴猴33 学习方法
    大学开学，就意味着又回到了被线性代数、大学物理等测验题折磨的状态了……网站无法手动输入题干公式，初高中用过的搜题软件又都搜不到，想找个答案解析仿佛在大海捞针！不过不用怕，今天小林就把从大学攒到毕业工作都在使用的搜题秘籍分享给大家。1.东西题库这是一个网站为学校教师提供试题试卷、课件及教案等服务的题库资源共享型网站，由必刷题、必刷卷教研团队研发与审核，涵盖初高中全学段、全学科教学资源，旨在帮助教师精
  • 香河吃肉饼 素面lhw
    图片发自App今天下午hx数学分析期中考试，所以周五没回家，今天下午我们开车接上hx，直奔香河去吃肉饼。香河是河北廊坊的一个县，夹在北京和天津之间，最有名的就是香河肉饼了。相传这是游牧民族突厥族用来招待贵客的食物，又叫突厥饼。因为突厥族牛羊肉多，面食少，所以贵客来了，主人便做面食，但把皮做的非常薄，后来皮薄馅足成了香河肉饼的特点。因了香河的位置，香河肉饼又叫京东肉饼。香河离北京也就一百多公里，以前
  • 中国数学必须思考的问题：现代数学体系下如何翻身做主人 刘亦叙 数学建模
    这个观点我说了十多年，我一直希望能唤醒中国数学！现代数学有三大核心：几何、代数、数学分析，数学分析就是微积分，也是三大核心的主体。几何与代数属于人类的古老数学，从远古到1977年，它们都是中华数学的优势与长项；微积分诞生于17世纪后半叶的欧洲，18世纪在欧拉等人的推广下迅速成为欧系的主体理论，欧拉名下的数学研究大多以微积分为工具，可以说欧拉与微积分是相互推动相互帮助。微积分是纯粹数学的标志，纯粹数
  • 集合 庵下桃花仙
    集合是一种无序且元素唯一的容器。可通过set函数或大括号创建。In[20]:set([2,2,2,1,3,3])Out[20]:{1,2,3}In[21]:{2,2,2,1,3,3}Out[21]:{1,2,3}集合支持数学上的集合操作，如联合、交集、差集、对称差集等。集合的元素也必须是不可变的。用到时，查阅《利用Python进行数学分析》68页即可。
  • 如何培养数感 潘雨恬
    本书名为《发展儿童数学关键能力》，那什么是数学关键能力？本书筛选了7个儿童的关键能力：数感，符号意识，运算能力，空间观念，数学分析观念，推理能力和模型思想。那么，如何培养数感？一、结合熟悉的生活情境培养数感1.创设童话情境培养数感数感发展的关键期是小学低年级，对于低年级的儿童我们可以创设这样的童话情景。如谁是“1”的好朋友，用找好朋友这样的形式，让低年级学生更丰富认识“1”。其实这样的情景不止是儿
  • 分析打卡day6 多元化数学喵
    学习中科大数学分析习题课讲义第三章今天是A组和B组，其实原本C组也能看完，奈何B站太好看啦。呜呜,嗷嗷嗷
  • 【新书推荐】3.1节 布尔运算 bcdaren 《X86汇编语言程序设计》汇编
    本节内容：布尔运算，又称为逻辑运算或位运算。■布尔代数：and与、or或、not非、xor异或，按位运算。3.1.1布尔代数■布尔代数与二进制的关系乔治·布尔是一位英国小学数学老师，19世纪最重要的数学家之一。出版了《逻辑的数学分析》，这是他对符号逻辑的第一次贡献。1854年，他出版了《思维规律的研究》，这是他最著名的著作。在这本书中布尔介绍了现在以他的名字命名的布尔代数。布尔代数非常简单，tru
  • 业余爱好-生物信息学/生物化学/物理/统计学/政治/数学/概率论/AI/AGI/区块链 amingMM 概率论
    生物信息学高等数学—元素和极限-实数的定义高等数学—元素和极限-实数的元素个数高等数学—元素和极限-自然数个数少于实数个数高等数学—元素和极限-无穷大之比较高等数学—元素和极限-级数的收敛高等数学—元素和极限-极限的定义数学分析与概率论人工智能AI数学基础——全套第一章高等数学基础：0-课程简介第一章高等数学基础：1-函数第一章高等数学函数：2-极限生物学、计算机科学、数学、英语生物学占总分的30
  • python机器学习算法进阶视频教程 24课 适合进阶学习 高清课件代码全 花心五花肉
    课程介绍：机器学习是人工智能的一个分支。我们使用计算机设计一个条统，使它能够根据提供的训练数据按照一定的方式来学习；随着训练次数的增加，该条统可以在性能上不新学习和改进；通过参数优化的学习模型，能够用于预测相关问题的输出。授课时长：48小时授课环境：Python3配套资料：高清视频、课件讲义、源码课程目录：01.第一课：机器学习与数学分析02.第二课：概率论与贝叶斯先验03.第三课：矩阵和线性代数
  • java 黑皇后_蓝桥杯java 基础练习 Sine之舞 树瓜 java黑皇后
    问题描述最近FJ为他的奶牛们开设了数学分析课，FJ知道若要学好这门课，必须有一个好的三角函数基本功。所以他准备和奶牛们做一个“Sine之舞”的游戏，寓教于乐，提高奶牛们的计算能力。不妨设An=sin(1–sin(2+sin(3–sin(4+...sin(n))...)Sn=(...(A1+n)A2+n-1)A3+...+2)An+1FJ想让奶牛们计算Sn的值，请你帮助FJ打印出Sn的完整表达式，以
  • 对奇迹变得笃信-《启动大脑》第3章 蓝熵
    以前一直觉得自己智商水平中等，并且对智商值超高的那些人充满崇拜，甚至有种遥不可及的仰望之感，对于用数值来评测智商这一概念从未产生过质疑，对人的评价也仅仅停留在高智商、高情商等几种极其有限标准之内，但今天才发现，原来数值智商并不能真实全面的的反应一个人的智力水平，与此同时，智商也并不仅限于学习能力、记忆能力、数学分析能力、语言表达等几个方面，而是涵盖个人、社会、创造、感官等诸多门类！以前对奇迹这个词
  • 常系数微分方程组的V函数构造定理的解释 a03910 笔记
    这是王高雄里的常微分方程里的二次型V函数的构造…一节的定理，定正矩阵，这个书里没注意到在哪，不过在高等代数中就是正定矩阵的意思，第二个划线部分矩阵里的微分运算，也是没见过的，看起来很有意思，但是原因呢？之前在证明刘维尔公式的时候有行列式求导运算，现在又有矩阵求导，其实没有特别的理由，就当作是一般的函数乘积求导而已，不过对于矩阵，只需要看作是n^2维向量值函数而已，然后按照数学分析中的多元函数微分即
  • 填鸭式学习与破案式学习 魏佳斌
    读“微积分的历程”，回顾数学史这一段波澜壮阔的开拓历史。离开学校多年，微积分基本已经还给老师，当然也表明当年学得并不扎实。比较感慨，我相信高数，尤其是大一的微积分，估计是好多同学的噩梦。更何况，我们当年数学系，学的可不是微积分，而是数学分析。数三的微积分，大部分都是计算，定理背后经常有两字：证略。而数学系的数学分析课，全部都是定理证明，基本就是重温当年牛顿、莱布尼茨，泰勒，柯西等大师走过的心路历程
  • 2018-09-26 yeshan333
    体验markdown添加链接我的博客添加图片百度上找的一级引用要判断一个人是否真正聪明，那就要看他能否根本不用动手，而工作却又能完成。二级引用在C++里,想搬起石头砸自己的脚更为困难了。不过一旦你真这么做了,整条腿都得报销!列表的使用一级列表pythonJavac++多级列表数学分析高等代数解析几何插入代码行内代码printf("helloworld");块代码,每行代码前四个空格或一个tabWo
  • 百闻不如一见，实验动手“再创造” ——我为“实验教学法”代言 椰没烦恼
    一、什么是实验教学法？实验教学法指的是教师借助仪器、多媒体设备等手段，在严谨的数学思想和理论的指导下，以数学素材为实验对象，引导学生对现实生活中与数量和图形有关的问题进行数学分析、操作、归纳总结，以实现理解数学、解释数学、应用数学为目的的教学活动。实验教学法由梅伊曼、拉伊提出。二、实验教学法的步骤1.编写实验计划。实验计划应在学年或学期开始时完成。其内容包括:实验课题、先后顺序、实验所需仪器设备等
  • 我与考研的结缘 茯苓_fuling
    距离考研结束已经过去4个月了，时间隔的有点久，一时间要谈起这一路走来的点点滴滴，并没有什么好的句子铺垫，我就追随我记忆为来谈吧。我记得，我初次了解到考研是在大一的课堂上。起因是我高考考的并不好，一直愧对父母，想着大学里应该认真学习，因此数学分析等主专业成绩还行，我对大学数学的兴趣还蛮大的，课后还经常请教老师，那时老师看出了我对数学的喜爱，便细细和我道尽考研的事情，我才知道我还有一次机会弥补高考的缺
  • 概率,概率分布,高斯分布,高维高斯分布 OwnResponsibility 数学基础知识SLAM概率论python
    文章目录前言一、概率与概率密度二、高斯分布是什么？三、高维高斯分布总结前言高斯分布的理解,它在低维和高维的形式。一、概率与概率密度两个基本的概念:概率:在某事件出现某一结果的可能性大小。分布:考虑事件的所有可能性那么它就是分布。分布函数，是概率统计中重要的函数，正是通过它，可用数学分析的方法来研究随机变量。分布函数是随机变量最重要的概率特征，分布函数可以完整地描述随机变量的统计规律，并且决定随机变
  • 中级C++：哈希 Keflavík C++哈希算法c++数据结构
    文章目录前言哈希冲突闭散列线性探测插入查找、删除开散列析构仿函数插入查找、删除迭代器封装成unordered_map、unordered_set编者寄语前言以前的计数排序就是一种哈希结构，通过直接映射，或者间接映射；通过对pair中的K进行取模、直接定制法（一元一次方程：Hash（Key）=A*Key+B））、平方取中法、数学分析法、随机数法、折叠法等等一系列方法，把K映射到一个vector数组上
  • 曲线积分和曲面积分 抄书侠
    图片发自App图片发自App图片发自App数学分析题解精粹1006.计算1002.求，其中为以为圆心，为半径的圆周()表示逆时针方向。1013.设是中的有界区域，其体积为，关于平面对称，的边界是光滑闭曲面，是的外向法矢与正轴的夹角，求1014.计算其中为连续函数，为平面在第四卦限上侧1015.计算其中是曲面与的交线。1025.证明1026.证明：式中光滑曲线包围着有界域，为沿着的外法线的导函数，1
  • 开始写你的技术博客吧 Foina数据分析狮
    我来讲讲自己的经历吧。大学和研究生都是数学专业的，那手推公式是家常便饭，比如，大学课程数学分析经常要证明定理，研究生课程泛函分析老师不按照课本讲，经常自己准备讲义，两节课可能只推导一个公式，么得办法，我们就跟着记跟着抄。研究生我做的课题通俗点讲就是解方程，为啥选这个课题？因为我喜欢手推公式。我研究生的论文就解了两个方程，手写的推导过程笔记已经找不到啦，想缅怀岁月都没有东西可以寄托。刚参加工作时，我
  • 二分查找排序算法 周凡杨 java二分查找排序算法折半
    一：概念 二分查找又称 折半查找（ 折半搜索/ 二分搜索），优点是比较次数少，查找速度快，平均性能好；其缺点是要求待查表为有序表，且插入删除困难。因此，折半查找方法适用于不经常变动而 查找频繁的有序列表。首先，假设表中元素是按升序排列，将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表 分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步
  • java中的BigDecimal bijian1013 javaBigDecimal
            在项目开发过程中出现精度丢失问题，查资料用BigDecimal解决，并发现如下这篇BigDecimal的解决问题的思路和方法很值得学习，特转载。         原文地址：http://blog.csdn.net/ugg/article/de
  • Shell echo命令详解 daizj echoshell
    Shell echo命令 Shell 的 echo 指令与 PHP 的 echo 指令类似，都是用于字符串的输出。命令格式： echo string 您可以使用echo实现更复杂的输出格式控制。 1.显示普通字符串: echo "It is a test" 这里的双引号完全可以省略，以下命令与上面实例效果一致： echo Itis a test 2.显示转义
  • Oracle DBA 简单操作 周凡杨 oracle dba sql
    --执行次数多的SQL select sql_text,executions from (      select sql_text,executions from v$sqlarea order by executions desc      ) where rownum<81;  &nb
  • 画图重绘 朱辉辉33 游戏
      我第一次接触重绘是编写五子棋小游戏的时候，因为游戏里的棋盘是用线绘制的，而这些东西并不在系统自带的重绘里，所以在移动窗体时，棋盘并不会重绘出来。所以我们要重写系统的重绘方法。   在重写系统重绘方法时，我们要注意一定要调用父类的重绘方法，即加上super.paint(g)，因为如果不调用父类的重绘方式，重写后会把父类的重绘覆盖掉，而父类的重绘方法是绘制画布，这样就导致我们
  • 线程之初体验 西蜀石兰 线程
    一直觉得多线程是学Java的一个分水岭，懂多线程才算入门。 之前看《编程思想》的多线程章节，看的云里雾里，知道线程类有哪几个方法，却依旧不知道线程到底是什么？书上都写线程是进程的模块，共享线程的资源，可是这跟多线程编程有毛线的关系，呜呜。。。 线程其实也是用户自定义的任务，不要过多的强调线程的属性，而忽略了线程最基本的属性。 你可以在线程类的run()方法中定义自己的任务，就跟正常的Ja
  • linux集群互相免登陆配置 林鹤霄 linux
    配置ssh免登陆 1、生成秘钥和公钥    ssh-keygen -t rsa 2、提示让你输入，什么都不输，三次回车之后会在~下面的.ssh文件夹中多出两个文件id_rsa 和 id_rsa.pub    其中id_rsa为秘钥，id_rsa.pub为公钥，使用公钥加密的数据只有私钥才能对这些数据解密    c
  • mysql : Lock wait timeout exceeded; try restarting transaction aigo mysql
    原文：http://www.cnblogs.com/freeliver54/archive/2010/09/30/1839042.html   原因是你使用的InnoDB   表类型的时候, 默认参数:innodb_lock_wait_timeout设置锁等待的时间是50s, 因为有的锁等待超过了这个时间,所以抱错.   你可以把这个时间加长,或者优化存储
  • Socket编程 基本的聊天实现。 alleni123 socket
    public class Server { //用来存储所有连接上来的客户 private List<ServerThread> clients; public static void main(String[] args) { Server s = new Server(); s.startServer(9988); } publi
  • 多线程监听器事件模式(一个简单的例子) 百合不是茶 线程监听模式
        多线程的事件监听器模式   监听器时间模式经常与多线程使用,在多线程中如何知道我的线程正在执行那什么内容,可以通过时间监听器模式得到        创建多线程的事件监听器模式 思路:    1, 创建线程并启动,在创建线程的位置设置一个标记     2,创建队
  • spring InitializingBean接口 bijian1013 javaspring
    spring的事务的TransactionTemplate，其源码如下： public class TransactionTemplate extends DefaultTransactionDefinition implements TransactionOperations, InitializingBean{ ... } TransactionTemplate继承了DefaultT
  • Oracle中询表的权限被授予给了哪些用户 bijian1013 oracle数据库权限
            Oracle查询表将权限赋给了哪些用户的SQL，以备查用。 select t.table_name as "表名", t.grantee as "被授权的属组", t.owner as "对象所在的属组"
  • 【Struts2五】Struts2 参数传值 bit1129 struts2
    Struts2中参数传值的3种情况 1.请求参数绑定到Action的实例字段上 2.Action将值传递到转发的视图上 3.Action将值传递到重定向的视图上   一、请求参数绑定到Action的实例字段上以及Action将值传递到转发的视图上 Struts可以自动将请求URL中的请求参数或者表单提交的参数绑定到Action定义的实例字段上，绑定的规则使用ognl表达式语言
  • 【Kafka十四】关于auto.offset.reset[Q/A] bit1129 kafka
    I got serveral questions about  auto.offset.reset. This configuration parameter governs how  consumer read the message from  Kafka when  there is no initial offset in ZooKeeper or
  • nginx gzip压缩配置 ronin47 nginx gzip 压缩范例
    nginx gzip压缩配置 更多 0 nginx gzip 配置   随着nginx的发展，越来越多的网站使用nginx，因此nginx的优化变得越来越重要，今天我们来看看nginx的gzip压缩到底是怎么压缩的呢？ gzip(GNU-ZIP)是一种压缩技术。经过gzip压缩后页面大小可以变为原来的30%甚至更小，这样，用
  • java-13.输入一个单向链表，输出该链表中倒数第 k 个节点 bylijinnan java
    two cursors. Make the first cursor go K steps first. /* * 第 13 题：题目：输入一个单向链表，输出该链表中倒数第 k 个节点 */ public void displayKthItemsBackWard(ListNode head,int k){ ListNode p1=head,p2=head;
  • Spring源码学习-JdbcTemplate queryForObject bylijinnan javaspring
    JdbcTemplate中有两个可能会混淆的queryForObject方法： 1. Object queryForObject(String sql, Object[] args, Class requiredType) 2. Object queryForObject(String sql, Object[] args, RowMapper rowMapper) 第1个方法是只查
  • [冰川时代]在冰川时代,我们需要什么样的技术? comsci 技术
         看美国那边的气候情况....我有个感觉...是不是要进入小冰期了?      那么在小冰期里面...我们的户外活动肯定会出现很多问题...在室内呆着的情况会非常多...怎么在室内呆着而不发闷...怎么用最低的电力保证室内的温度.....这都需要技术手段...   &nb
  • js 获取浏览器型号 cuityang js浏览器
    根据浏览器获取iphone和apk的下载地址 <!DOCTYPE html> <html> <head>     <meta charset="utf-8" content="text/html"/>     <meta name=
  • C# socks5详解 转 dalan_123 socketC#
    http://www.cnblogs.com/zhujiechang/archive/2008/10/21/1316308.html  这里主要讲的是用.NET实现基于Socket5下面的代理协议进行客户端的通讯，Socket4的实现是类似的，注意的事，这里不是讲用C#实现一个代理服务器，因为实现一个代理服务器需要实现很多协议，头大，而且现在市面上有很多现成的代理服务器用，性能又好，
  • 运维 Centos问题汇总 dcj3sjt126com 云主机
    一、sh 脚本不执行的原因 sh脚本不执行的原因 只有2个 1.权限不够 2.sh脚本里路径没写完整。   二、解决You have new mail in /var/spool/mail/root 修改/usr/share/logwatch/default.conf/logwatch.conf配置文件 MailTo = MailFrom   三、查询连接数
  • Yii防注入攻击笔记 dcj3sjt126com sqlWEB安全yii
    网站表单有注入漏洞须对所有用户输入的内容进行个过滤和检查，可以使用正则表达式或者直接输入字符判断，大部分是只允许输入字母和数字的，其它字符度不允许；对于内容复杂表单的内容，应该对html和script的符号进行转义替换：尤其是<,>,',"",&这几个符号 这里有个转义对照表： http://blog.csdn.net/xinzhu1990/articl
  • MongoDB简介[一] eksliang mongodbMongoDB简介
    MongoDB简介 转载请出自出处：http://eksliang.iteye.com/blog/2173288 1.1易于使用        MongoDB是一个面向文档的数据库，而不是关系型数据库。与关系型数据库相比，面向文档的数据库不再有行的概念，取而代之的是更为灵活的“文档”模型。        另外，不
  • zookeeper windows 入门安装和测试 greemranqq zookeeper安装分布式
    一、序言       以下是我对zookeeper 的一些理解：      zookeeper 作为一个服务注册信息存储的管理工具，好吧，这样说得很抽象，我们举个“栗子”。       栗子1号：       假设我是一家KTV的老板，我同时拥有5家KTV，我肯定得时刻监视
  • Spring之使用事务缘由(2-注解实现) ihuning spring
      Spring事务注解实现   1. 依赖包：     1.1 spring包：           spring-beans-4.0.0.RELEASE.jar           spring-context-4.0.0.
  • iOS App Launch Option 啸笑天 option
    iOS 程序启动时总会调用application:didFinishLaunchingWithOptions:，其中第二个参数launchOptions为NSDictionary类型的对象，里面存储有此程序启动的原因。   launchOptions中的可能键值见UIApplication Class Reference的Launch Options Keys节 。 1、若用户直接
  • jdk与jre的区别（_） macroli javajvmjdk
    简单的说JDK是面向开发人员使用的SDK，它提供了Java的开发环境和运行环境。SDK是Software Development Kit 一般指软件开发包，可以包括函数库、编译程序等。  JDK就是Java Development Kit JRE是Java Runtime Enviroment是指Java的运行环境，是面向Java程序的使用者，而不是开发者。 如果安装了JDK，会发同你
  • Updates were rejected because the tip of your current branch is behind qiaolevip 学习永无止境每天进步一点点众观千象git
    $ git push joe prod-2295-1 To [email protected]:joe.le/dr-frontend.git ! [rejected] prod-2295-1 -> prod-2295-1 (non-fast-forward) error: failed to push some refs to '[email protected]
  • [一起学Hive]之十四-Hive的元数据表结构详解 superlxw1234 hivehive元数据结构
    关键字：Hive元数据、Hive元数据表结构   之前在 “[一起学Hive]之一–Hive概述，Hive是什么”中介绍过，Hive自己维护了一套元数据，用户通过HQL查询时候，Hive首先需要结合元数据，将HQL翻译成MapReduce去执行。 本文介绍一下Hive元数据中重要的一些表结构及用途，以Hive0.13为例。   文章最后面，会以一个示例来全面了解一下，
  • Spring 3.2.14，4.1.7，4.2.RC2发布 wiselyman Spring 3
      Spring 3.2.14、4.1.7及4.2.RC2于6月30日发布。   其中Spring 3.2.1是一个维护版本(维护周期到2016-12-31截止)，后续会继续根据需求和bug发布维护版本。此时，Spring官方强烈建议升级Spring框架至4.1.7 或者将要发布的4.2 。   其中Spring 4.1.7主要包含这些更新内容。
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他