实验: 电磁波的反射干涉
实验:静电场的边值问题
实验:带电粒子在磁场中的受力
实验:电磁波的极化
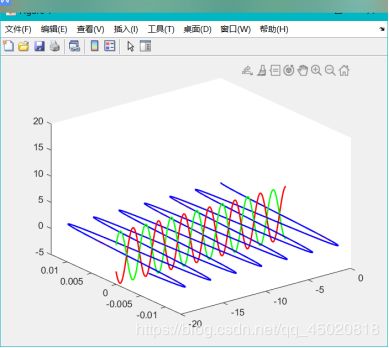
1. 平面电磁波向理想导体垂直入射的仿真
Matlab代码(静态效果):
miu1=4*pi*1e-7;
epsilong1=1e-9/(36*pi);
Ei0=5;
w=2*pi*1e8;
z=[-20:0.1:0];
m0=zeros(size(z));
k1=w*sqrt(miu1*epsilong1);
niu1=sqrt(miu1/epsilong1);
t=100;
Ei=Ei0*cos(w*t-k1*z);
Hi=Ei0*cos(w*t-k1*z)/niu1;
Er0=-Ei0;
Er=Er0*cos(w*t+k1*z);
Hr=-Er0*cos(w*t+k1*z)/niu1;
plot3(z,m0,Ei,'r','LineWidth',1.5);
hold on
plot3(z,Hi,m0,'r','LineWidth',1.5);
hold on
plot3(z,m0,Er,'g','LineWidth',1.5);
hold on
plot3(z,Hr,m0,'b','LineWidth',1.5);
hold on
plot3(0,0,20,'LineWidth',1.5);
Matlab代码(动态模拟):
u0=4*pi*1e-7;%磁导率
e0 = 1e-9/(36*pi);%电介质常数
Z0 = (u0/e0)^0.5;%波阻抗
f = 6*1e7; %入射波频率
w = 2*pi*f;%入射波角频率
k = w*(u0*e0)^0.5;%波数
phi_E = 0;%电场初始相位
phi_H = 0;%磁场初始相位
EE = 20;%电场幅度
HH = EE/Z0;%磁场幅度
x = 0:0.1:20;%横坐标序列
m0 = zeros(size(x));
y0 = -20:1:20;
m1 = zeros(size(y0));
z0 = -0.05:0.01:0.05;
m2 = zeros(size(z0));
gifname = 'c:\users\pxo\desktop\mag_motion.gif';%动态图输出路径
figure
for t=0:200
Ez = -EE*cos(k*x+w*t*1e-9+phi_E);%入射波电场幅度序列
Er = EE*cos(k*x-w*t*1e-9+phi_E);%反射波电场幅度序列
Hr = -HH*cos(k*x+w*t*1e-9+phi_H);%反射波磁场幅度序列
Hy = -HH*cos(k*x+w*t*1e-9+phi_H);%入射波磁场幅度序列
yy = -20:20;
zz = ones(size(yy))*0;
[yy, zz] = meshgrid(yy,zz);
xx = yy*0+20;
mesh(xx,yy,zz,'FaceColor','g');
hold on
plot3(x,m0,m0,'black','Linewidth',3);
hold on
plot3(m1+20,y0,m1,'black','Linewidth',1.5);
hold on
plot3(m2+20,m2,z0,'black','Linewidth',1.5);
hold on
plot3(x,Ez,m0,'r','LineWidth',1.2);
hold on
plot3(x,m0,Hy,'b','LineWidth',1.2);
hold on
plot3(x,m0,Hr,'c','LineWidth',1.2);
hold on
plot3(x,Er,m0,'green','LineWidth',1.2);
hold off
xlabel('传播方向');
ylabel('电场Ey');
zlabel('磁场Hz');
title(['平面电磁波传播示意图','t=',num2str(t),'ns'],'fontsize',14)
set(gca,'fontsize',12)
drawnow
%一下是保存动态图部分
frame = getframe(1);
im = frame2im(frame);
[imind, cm] = rgb2ind(im,256);
if t==0
imwrite(imind, cm, gifname, 'gif', 'WriteMode', 'overwrite', 'Loopcount', inf);
else
imwrite(imind, cm ,gifname, 'gif', 'WriteMode', 'append', 'DelayTime', 0.1);
end
end

2. 平面电磁波向理想介质垂直入射的仿真
MATLAB代码
miu1=4*pi*1e-7;
miu2=6*pi*1e-7;
epsilong1=1e-9/(36*pi);
epsilong2=2e-9/(36*pi);
Ei0=5;
w=2*pi*1e8;
k1=w*sqrt(miu1*epsilong1);
niu1=sqrt(miu1/epsilong1);
k2=w*sqrt(miu2*epsilong2);
niu2=sqrt(miu2/epsilong2);
Et0=Ei0*2*niu2/(niu2+niu1);
Er0=Ei0*(niu2-niu1)/(niu2+niu1);
z=[-20:0.1:0];
z1=[0:0.1:20];
m0=zeros(size(z));
t=100;
Ei=Ei0*cos(w*t-k1*z);
Hi=Ei0*cos(w*t-k1*z)/niu1;
Er=Er0*cos(w*t+k1*z);
Hr=-Er0*cos(w*t+k1*z)/niu1;
Et=Et0*cos(w*t-k2*z1);
Ht=Et0*cos(w*t-k2*z1)/niu2;
plot3(Ei,z,m0);
hold on
plot3(m0,z,Hi);
hold on
plot3(Er,z,m0);
hold on
plot3(m0,z,Hr);
hold on
plot3(Et,z1,m0);
hold on
plot3(m0,z1,Ht);



