理解OFDM技术原理
一、为什么要用OFDM？
通信有一个长期的用户需求——快，但是又受到可用电磁频谱的物理限制——少，因而如何在较少可用的频谱上更快的传输信息一直是通信技术发展的核心驱动力。
常用的单载波传输（如ASK，FSK，和PSK等）在一个符号传输中使用单个载波承载信息，因而速率较低。想要提高传输速度，需要缩短码元持续时间，对频带宽度需求增加，对均衡器和均衡算法要求提高，实现困难。
因而很自然地考虑将频带进行划分，实现一段时域信号中包含多个频段的信号分量（如下图），不同频段的信号承载不同的信息，可以实现多路信号的并行传输，常用的技术有FDM和OFDM。
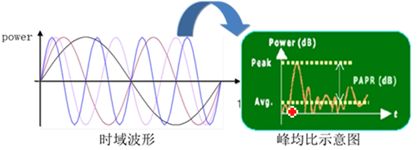
FDM将频谱分割成多块，并在多块之间设置保护带宽。这是因为，保护带宽可以避免不同频段之间相互干扰，且便于使用滤波器的调制解调（滤波器一般为非理想，也即滤波器边沿不会很陡峭），但这样会造成频带利用率下降。
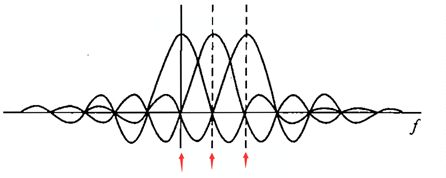
OFDM技术就正面直视并解决了这种载波相互干扰的问题，是 一种频带使用更加紧凑的特殊FDM ，如下图。OFDM的解决方法就是引入了正交的特性，这里正交的意思是，下图中频域采样点（红色箭头）只与当前载波频率有关，不受其他载波影响。这样就可以在有较高频带利用率的情况下并行发送更多信息，也可以说：OFDM技术可以在较少带宽中更快的发送信息。
二、如何实现OFDM？
如何才能让信号具有上图所示的OFDM频带正交的特点呢？请先看下面两个信号的构造过程：
上面两个图都表示，无限长周期正弦信号与同等长度的矩形门函数相乘得到我们常看到的被截断的有限长载波信号，于此同时频域完成频谱的卷积过程得到中心频点不同的形状相同的sinc函数。如果将上图两个实传信号相加，其频谱可如下图所示：
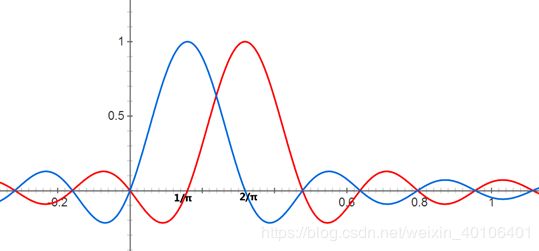
先不用关心他们的横坐标对应的数值，上面这个实验给我们启发：选取一个长度为 T s {{T}_{s}} Ts的矩形窗函数乘以不同频率的正弦信号（或余弦信号）就可得到OFDM波形。通过傅里叶变换的知识，我们可以知道，矩形窗函数的长度 T s {{T}_{s}} Ts决定着sinc函数的中心频点距离第一零点的距离 Δ f \Delta f Δf，如下图所示（左侧时域，右侧频域）：
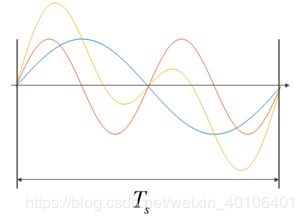
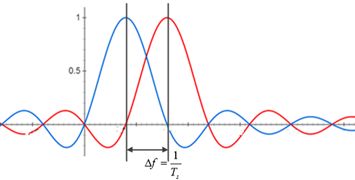
总的来说，要想实现OFDM，只需要满足各相邻子载波的频率最小间隔满足 Δ f = 1 T s \Delta f=\frac{1}{{{T}_{s}}} Δf=Ts1。
注意:
- 这里只是在讲多载波频率如何设置，没有说幅度和相位的问题，因而可以引入PSK和QAM技术对ODFM进一步加速！
- 上述为基带信号，实际场景在发送前还需要把基带信号调制到相应的频段上才能发射出去。
三、 OFDM的工程化实现
方法一：
基带ODFM信号表达式： z ( t ) = ∑ k = 0 N − 1 B k cos ( 2 π f k t ) z\left( t \right)=\sum\limits_{k=0}^{N-1}{{{B}_{k}}\cos \left( 2\pi {{f}_{k}}t \right)} z(t)=k=0∑N−1Bkcos(2πfkt)
为了可承载很多的信息比特， z ( t ) = ∑ k = 0 N − 1 B k e 2 π f k t z\left( t \right)=\sum\limits_{k=0}^{N-1}{{{\mathbf{B}}_{k}}{{e}^{2\pi {{f}_{k}}t}}} z(t)=k=0∑N−1Bke2πfkt，其中 B k = a k + j b k {{\mathbf{B}}_{k}}={{a}_{k}}+j{{b}_{k}} Bk=ak+jbk
展开后可以得到：
Re { z ( t ) } = ∑ k = 0 N − 1 a k cos ( 2 π f k t ) − b k s i n ( 2 π f k t ) \operatorname{Re}\left\{ z\left( t \right) \right\}=\sum\limits_{k=0}^{N-1}{{{a}_{k}}\cos \left( 2\pi {{f}_{k}}t \right)-{{b}_{k}}sin\left( 2\pi {{f}_{k}}t \right)} Re{z(t)}=k=0∑N−1akcos(2πfkt)−bksin(2πfkt)
Im { z ( t ) } = ∑ k = 0 N − 1 a k s i n ( 2 π f k t ) + b k cos ( 2 π f k t ) \operatorname{Im}\left\{ z\left( t \right) \right\}=\sum\limits_{k=0}^{N-1}{{{a}_{k}}sin\left( 2\pi {{f}_{k}}t \right)+{{b}_{k}}\cos \left( 2\pi {{f}_{k}}t \right)} Im{z(t)}=k=0∑N−1aksin(2πfkt)+bkcos(2πfkt)
OFDM射频信号：
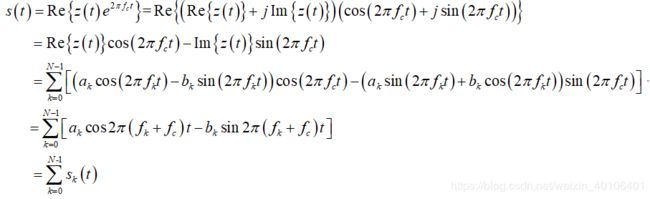其中， s k ( t ) = a k cos 2 π ( f k + f c ) t − b k sin 2 π ( f k + f c ) t {{s}_{k}}\left( t \right)={{a}_{k}}\cos 2\pi \left( {{f}_{k}}+{{f}_{c}} \right)t-{{b}_{k}}\sin 2\pi \left( {{f}_{k}}+{{f}_{c}} \right)t sk(t)=akcos2π(fk+fc)t−bksin2π(fk+fc)t
依赖上面推导，可以使用的调制解调架构如下：
通过以上这种方法来实现OFDM信号并发射出去需要耗费很多的混频器，且要求正弦振荡器和余弦振荡器严格正交，工程实现起来很困难，因而出现了下面基于DFT和IDFT的方法。
方法二：
OFDM基带信号 z ( t ) = ∑ k = 0 N − 1 B k e 2 π f k t z\left( t \right)=\sum\limits_{k=0}^{N-1}{{{\mathbf{B}}_{k}}{{e}^{2\pi {{f}_{k}}t}}} z(t)=k=0∑N−1Bke2πfkt和IDFT变换 x [ n ] = 1 N ∑ k = 0 N − 1 X [ k ] e j 2 π k N n x\left[ n \right]=\frac{1}{N}\sum\limits_{k=0}^{N-1}{X\left[ k \right]{{e}^{j2\pi \frac{k}{N}n}}} x[n]=N1k=0∑N−1X[k]ej2πNkn在计算结构上很相似，且计算系数都为离散复数 B k {{\mathbf{B}}_{k}} Bk和 X [ k ] X\left[ k \right] X[k]（这里不考虑固定系数 1 N \frac{1}{N} N1的影响，但不同点在于OFDM基带表达式的输出为连续信号，而IDFT计算得到离散信号，因而他们之间相差一个D/A变换器，也即对IDFT输出信号进行D/A处理即可得到OFDM基带信号输出。
另外， 需要为实数（不包含虚部），因而需要根据DFT变换的性质，构造对称共轭的 B ′ k = [ B k , c o n j ( B k ) ] {{\mathbf{{B}'}}_{k}}=\left[ {{\mathbf{B}}_{k}},conj\left( {{\mathbf{B}}_{k}} \right) \right] B′k=[Bk,conj(Bk)]作为IDFT的输入。
IFFT和FFT是IDFT和DFT的快速实现方法，常用的有基2的FFT和基4的FFT，其通过蝶形运算大大简化了DFT的计算量。
基于FFT的OFDM调制解调方法如下：
- 辅助技术一：循环前缀和循环后缀
为了消除码间串扰（ISI）需要在两个OFDM符号之间引入保护间隔GI，如果采用全零的简单保护间隔会引起载波间干扰（ICI），最好的方法是需要添加循环前缀（CP），其长度约为OFDM符号长度的1/4~1/6。
通常我们只关注因相邻OFDM符号滞后引起的ISI而添加CP，在一些场景中也会有超前的情况，同样的道理需要添加循环后缀（CS）。
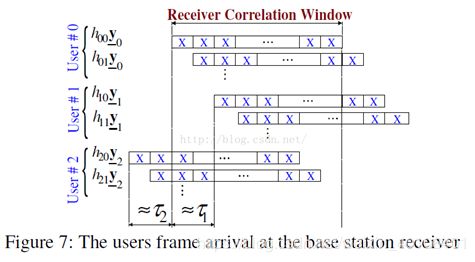相比于用户0，用户1和用户2分别有滞后和超前的情况，因而需要CP和CS同时使用，添加方法如下所示。
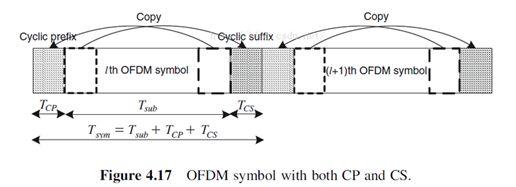
- 辅助技术二：余弦滚降窗
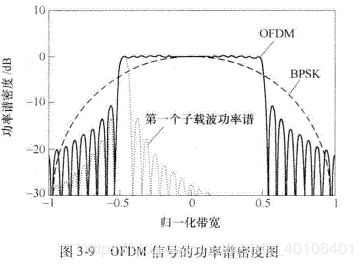
一个OFDM符号内的多个载波时域叠加，对应地，频域中多个sinc函数也会叠加，效果如下图所示。可见其频谱并不是个理想矩形，而是有明显的带外辐射现象。为了减弱这种带外辐射，需要对时域多载波叠加信号进行加窗处理，常用的加窗方法是加余弦窗函数。
四、基于FFT的OFDM实现Matlab代码
clear all;
close all;
carrier_count=200;
%这个程序中OFDM子载波个数为512，其中400即carrier_count*2为数据符号，其余赋0值。
symbols_per_carrier=20;%每个子载波上的符号数，在这里即为OFDM符号的个数。
bits_per_symbol=4;%OFDM符号的每个子载波上传输的比特数。4比特通常采用16QAM调制。
IFFT_bin_length=512;%FFT长度，也即一个OFDM符号的子载波的个数。
PrefixRatio=1/4;%循环前缀的比率，即循环前缀与OFDM符号长度的比值，通常在 1/6~1/4之间。
GI=PrefixRatio*IFFT_bin_length ;%保护间隔的长度，这里为128。
beta=1/32;%升余弦窗的滚降系数。
GIP=beta*(IFFT_bin_length+GI);%循环后缀的长度，这里为20
SNR=30; %本程序考虑加性高斯白噪声信道，这里信噪比为30dB。
%===============================OFDM信号产生=============================
baseband_out_length = carrier_count * symbols_per_carrier * bits_per_symbol;
%计算传输数据总的比特数，为200*20*4=16000比特。16000比特的构成为20个OFDM符号，每个OFDM
%符号200个子载波，每个子载波传输4比特信息。
carriers=(1:carrier_count)+(floor(IFFT_bin_length/4) - floor(carrier_count/2));
%计算OFDM符号子载波的序号，carriers中存放的序号是29~228。
conjugate_carriers = IFFT_bin_length - carriers + 2;
%计算OFDM符号子载波的序号，conjugate_carriers中存放的序号是282~481。
rand( 'twister',0)
baseband_out=round(rand(1,baseband_out_length));
%产生16000比特待传输的二进制比特流。这里存放的是发送的二进制信号与后面解调后的二进制信号比
%较，可以计算误码率。
%16QAM调制并绘制星座图
complex_carrier_matrix=qam16(baseband_out);
%调用子程序qam16进行16QAM调制。将baseband_out中的二进制比特流，每4比特转换为一个16QAM信
%号，即将二进制比特流每4比特转换为-3-3j、-3+3j、3-3j、3+3j、-1-3j、-1+3j、1-3j、1+3j、%-3-j、-3+j、3-j、3+j、-1-j、-1+j、1-j、1+j中的一个。转换后complex_carrier_matrix为%1*4000矩阵。
complex_carrier_matrix=reshape(complex_carrier_matrix',carrier_count,symbols_per_carrier)';
%转换complex_carrier_matrix中的数据为carrier_count*symbols_per_carrier矩阵，这里为%20*200矩阵。
figure(1);
plot(complex_carrier_matrix,'*r');% 绘制16QAM星座图
axis([-4, 4, -4, 4]);
title('16QAM调制后星座图');
grid on
%IFFT，即进行OFDM调制。
IFFT_modulation=zeros(symbols_per_carrier,IFFT_bin_length);
%将symbols_per_carrier*IFFT_bin_length矩阵赋0值，这里将20*512矩阵赋0值。这里512是%IFFT的长度，也是OFDM符号子载波的个数。
IFFT_modulation(:,carriers ) = complex_carrier_matrix ;
%将20*200的complex_carrier_matrix的数据赋给IFFT_modulation的第29~228列，即给512个子%载波中的29~229个子载波赋值。
IFFT_modulation(:,conjugate_carriers ) = conj(complex_carrier_matrix);
%将20*200的complex_carrier_matrix的数据赋给512个子载波中的第282~481个子载波。
%这段程序构造了512个子载波的OFDM符号，并且各个子载波上的数据是共轭对称的。这样做的目的是经过%IFFT后形成的OFDM符号均为实数。另外，在512个子载波中，仅有400个子载波为数据，其余为0值。相%当于补零，补零的目的是通常IFFT的长度应该为2的整数次幂。
signal_after_IFFT=ifft(IFFT_modulation,IFFT_bin_length,2);%IFFT实现OFDM调制。
time_wave_matrix=signal_after_IFFT;%
figure(2);
plot(0:IFFT_bin_length-1,time_wave_matrix(2,:));%画一个OFDM信号的时域表现
axis([0, 512, -0.4, 0.4]);
grid on;
ylabel('Amplitude');
xlabel('Time');
title('OFDM Time Signal, One Symbol Period');
%添加循环前缀与循环后缀
XX=zeros(symbols_per_carrier,IFFT_bin_length+GI+GIP);
%IFFT_bin_length+GI+GIP为OFDM、循环前缀、循环后缀长度之和。
for k=1:symbols_per_carrier
for i=1:IFFT_bin_length
XX(k,i+GI)=signal_after_IFFT(k,i);
end
for i=1:GI
XX(k,i)=signal_after_IFFT(k,i+IFFT_bin_length-GI);%添加循环前缀
end
for j=1:GIP
XX(k,IFFT_bin_length+GI+j)=signal_after_IFFT(k,j);%添加循环后缀
end
end
time_wave_matrix_cp=XX;%带循环前缀与循环后缀的OFDM符号。
figure(3);
plot(0:length(time_wave_matrix_cp)-1,time_wave_matrix_cp(2,:));
%画带循环前缀与循环后缀的OFDM信号的时域波形
axis([0, 600, -0.3, 0.3]);
grid on;
ylabel('Amplitude');
xlabel('Time');
title('OFDM Time Signal with CP, One Symbol Period');
%OFDM符号加窗
windowed_time_wave_matrix_cp=zeros(1,IFFT_bin_length+GI+GIP);
for i = 1:symbols_per_carrier
windowed_time_wave_matrix_cp(i,:) =real(time_wave_matrix_cp(i,:)).*rcoswindow(beta,IFFT_bin_length+GI)';
%调用rcoswindow产生升余弦窗，对带循环前缀与循环后缀的OFDM符号加窗。
end
figure(4);
plot(0:IFFT_bin_length-1+GI+GIP,windowed_time_wave_matrix_cp(2,:));
%画加窗后的OFDM符号
axis([0, 700, -0.2, 0.2]);
grid on;
ylabel('Amplitude');
xlabel('Time');
title('OFDM Time Signal Apply a Window , One Symbol Period');
%生成发送信号，并串变换
windowed_Tx_data=zeros(1,symbols_per_carrier*(IFFT_bin_length+GI)+GIP);
%注意并串变换后数据的长度为symbols_per_carrier*(IFFT_bin_length+GI)+GIP，这里考虑了循环前缀与循环后缀的重叠相加。
windowed_Tx_data(1:IFFT_bin_length+GI+GIP)=windowed_time_wave_matrix_cp(1,:);
%赋第一个加窗带循环前缀后缀的OFDM符号至windowed_Tx_data，即发送串行数据。
for i = 1:symbols_per_carrier-1
windowed_Tx_data((IFFT_bin_length+GI)*i+1:(IFFT_bin_length+GI)*(i+1)+GIP)=windowed_time_wave_matrix_cp(i+1,:);%并串变换，循环前缀与循环后缀重叠相加
end
Tx_data_withoutwindow=reshape(time_wave_matrix_cp',(symbols_per_carrier)*(IFFT_bin_length+GI+GIP),1)';
%不加窗数据并串变换
Tx_data=reshape(windowed_time_wave_matrix_cp',(symbols_per_carrier)*(IFFT_bin_length+GI+GIP),1)';
%加窗数据，但按照循环前缀与循环后缀不重叠相加进行并串变换。此时数据长度为%(symbols_per_carrier)*(IFFT_bin_length+GI+GIP)。
temp_time1 = (symbols_per_carrier)*(IFFT_bin_length+GI+GIP);
%加窗，循环前缀与循环后缀不重叠数据长度，即为发送的总的数据比特数
figure (5)
subplot(2,1,1);
plot(0:temp_time1-1,Tx_data );%画循环前缀与循环后缀不重叠相加OFDM信号的时域波形
grid on
ylabel('Amplitude (volts)')
xlabel('Time (samples)')
title('OFDM Time Signal')
temp_time2 =symbols_per_carrier*(IFFT_bin_length+GI)+GIP;
%加窗，循环前缀与循环后缀重叠相加数据长度
subplot(2,1,2);
plot(0:temp_time2-1,windowed_Tx_data);
%画循环前缀与循环后缀重叠相加OFDM信号的时域波形
grid on
ylabel('Amplitude (volts)')
xlabel('Time (samples)')
title('OFDM Time Signal')
%====================经过加性高斯白噪声信道=======----==================
Tx_signal_power = var(windowed_Tx_data);% 计算信号功率
linear_SNR=10^(SNR/10);% 转换对数信噪比为线性幅度值
noise_sigma=Tx_signal_power/linear_SNR;%计算噪声功率，也就是方差
noise_scale_factor = sqrt(noise_sigma);% 计算标准差
noise=randn(1,((symbols_per_carrier)*(IFFT_bin_length+GI))+GIP)*noise_scale_factor;% 产生功率为noise_scale_factor高斯噪声
Rx_data=windowed_Tx_data +noise;
%在发送数据上加噪声，相当于OFDM信号经过加性高斯白噪声信道。
%==========================OFDM信号解调===============================
Rx_data_matrix=zeros(symbols_per_carrier,IFFT_bin_length+GI+GIP);
%存放并行的接收数据
for i=1:symbols_per_carrier
Rx_data_matrix(i,:)=Rx_data(1,(i-1)*(IFFT_bin_length+GI)+1:i*(IFFT_bin_length+GI)+GIP);% 串并变换
end
Rx_data_complex_matrix=Rx_data_matrix(:,GI+1:GI+IFFT_bin_length);
% 去掉循环前缀与循环后缀，取出OFDM符号传输的数据
Y1=fft(Rx_data_complex_matrix,IFFT_bin_length,2);% 求FFT，即OFDM信号解调
Rx_carriers=Y1(:,carriers);
% 取出carriers序号对应的子载波上的发送数据，去掉加入的零及共轭对称部分
Rx_phase =angle(Rx_carriers);% 计算接收信号的相位特性
Rx_mag = abs(Rx_carriers);% 计算接收信号的幅度特性
[M, N]=pol2cart(Rx_phase, Rx_mag);%转换极坐标数据为直角坐标数据
Rx_complex_carrier_matrix = complex(M, N);%两个直角坐标的实数据为构成复数据。
figure(7);
plot(Rx_complex_carrier_matrix,'*r');%画接收信号的星座图
axis([-4, 4, -4, 4]);
title('SNR=30dB接收数据星座图');
grid on
function [complex_qam_data]=qam16(bitdata)
%输入参数：bitdata为二进制数码流
%输出参数：complex_qam_data为16QAM复信号
X1=reshape(bitdata,4,length(bitdata)/4)';%将二进制数码流以4比特分段
d=1;
%转换4比特二进制码为十进制码1~16，生成mapping映射表中的索引。
for i=1:length(bitdata)/4;
for j=1:4
X1(i,j)=X1(i,j)*(2^(4-j));
end
source(i,1)=1+sum(X1(i,:));
end
%16QAM映射表，该表中存放的是16对，每对两个实数，标识星座位置。
mapping=[-3*d 3*d; -d 3*d;d 3*d;3*d 3*d;-3*d d; -d d; d d;3*d d; -3*d -d; -d -d; d -d;3*d -d;-3*d -3*d;-d -3*d; d -3*d;3*d -3*d];
for i=1:length(bitdata)/4
qam_data(i,:)=mapping(source(i),:);%数据映射
end
complex_qam_data=complex(qam_data(:,1),qam_data(:,2));
%组合为复数形式，形成16QAM信号。
end
function [rcosw]=rcoswindow(beta, Ts)
%输入参数：beta为升余弦窗滚降系数，Ts为IFFT长度加循环前缀长度
t=0:(1+beta)*Ts;
rcosw=zeros(1,(1+beta)*Ts);
%计算升余弦窗，共有三部分
for i=1:beta*Ts;
rcosw(i)=0.5+0.5*cos(pi+ t(i)*pi/(beta*Ts));%计算升余弦窗第一部分
end
rcosw(beta*Ts+1:Ts)=1;%升余弦窗第二部分
for j=Ts+1:(1+beta)*Ts+1;
rcosw(j-1)=0.5+0.5*cos((t(j)-Ts)*pi/(beta*Ts));%计算升余弦窗第三部分
end
rcosw=rcosw';% 转换为列向量
end
参考文章：
- 《深入浅出通信原理》，陈爱军
- 《MIMO-OFDM系统原理、应用及仿真》，李莉
- 《通信原理》，樊昌信
- https://www.bilibili.com/video/BV12z411B7y9?from=search&seid=3227339177102192107
- https://blog.csdn.net/qq_16923717/article/details/83623571
- https://blog.csdn.net/rs_network/article/details/50682369
- https://blog.csdn.net/a493823882/article/details/80058002