OFDM调制理解

前言

因为要学习gnuradio的使用，然后要看他的一个例子是生成一串随机比特数据，然后经过OFDM调制后通过USRP发送出去。整了一下不是很明白这一过程，所以先弄清楚OFDM的调制过程吧。于是，复制卡卡西附体。把资料整理在这里，供以后方便查看（小声逼逼，期末来了没时间慢慢打字，所以还是截图放在这里快点）。
因为大都是截图来的，可能有些符号不统一。所以符号的话在一个小标题内是统一的，在大标题范围上就不一定了。

OFDM调制理解

OFDM调制

基本原理

正交频分复用（OFDM）的基本原理就是把高速的数据流通过串-并转换，分配到传输速率相对较低的若干个子信道中进行传输。由于每个子信道的的符号周期会相对增加，因此可以减小多径时延拓展对系统造成的影响。另一方面，还可以在OFDM符号间插入保护间隔，进一步降低或消除由多径时延带来的符号间干扰（ISI）。
OFDM是一种特殊的多载波复用（MCM）传输方案，可以被当作一种调制技术，也可以被当作一种复用技术。多载波传输把数据流分解成若干个子数据流，这样每个数据流将具有低的多的数据速率，用这样的低数据率符号再去调制相应的子载波，就构成多个低速率符号并行发送的传输系统。OFDM是对多载波调制的一种改进，基本思想就是把高速的数据流通过串-并转换成N路低速率并行数据流，然后对N路相互正交的载波进行调制。与传统的频分复用相比，OFDM的子载波正交复用技术大大提高了频带利用率。如图
简单的说OFDM 是一种多载波传输技术，N 个子载波把整个信道分割成 N 个子信道，N 个子信 道并行传输信息。

上面这副图是普通FDM的频谱图

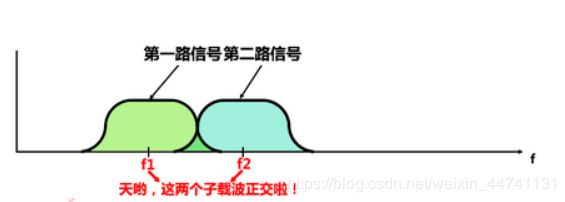
继续靠近就成OFDM的频谱图了，间隔频率互相正交，因此频谱虽然有重叠，但是仍然是没有互相干扰的。

OFDM系统组成

OFDM 系统的组成框图如下图 1.1 所示。
输入比特序列完成串并变换后，根据采用的调制方式，完成相应的调制映射，形成调制信息序列 ，对进行 IDFT，计算出 OFDM 已调信号的时域抽样序列，加上循环前缀 CP（循环前缀可以使 OFDM 系统完全消除信号的多径传播造成的符号间干扰（ISI）和载波间干扰（ICI）），再作 D/A 变换，得到 OFDM 已调信号的时 域波形。接收端先对接收信号进行 A/D 变换，去掉循环前缀 CP，得到 OFDM 已调信号的抽样序列，对该抽样序列作 DFT 即得到原调制信息序列 。

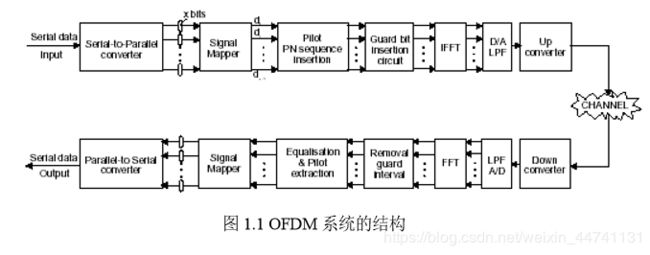
简单点即输入比特信号- - ->64QAM调制映射- - ->串并行转换- - ->得到N位调制信X（K）序列 - - ->对频域数据符号X(K)进行IFFT变换- - ->N位时域抽样信号X(N)- - ->加起来，加上循环前缀CP- - ->D/A转换- - ->发射
下面按照步骤一步步来：先调制

QAM调制映射

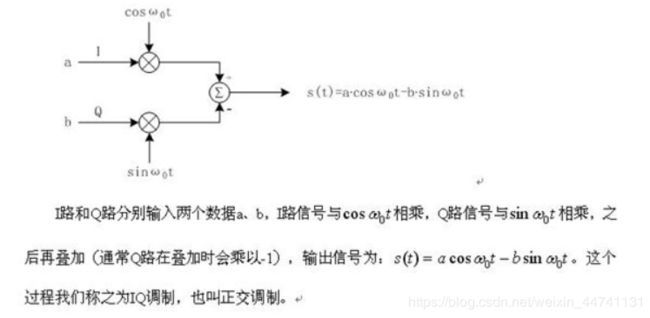
IQ调制

IQ信号与IQ调制有关，IQ调制也叫正交调制，调制原理如下：

输入正交调制器得信号一般被称为IQ信号，经常用复数来表示：a+jb,对应复平面上得一个点，因此IQ信号通常被大家称为“复信号”。
IQ解调原理:

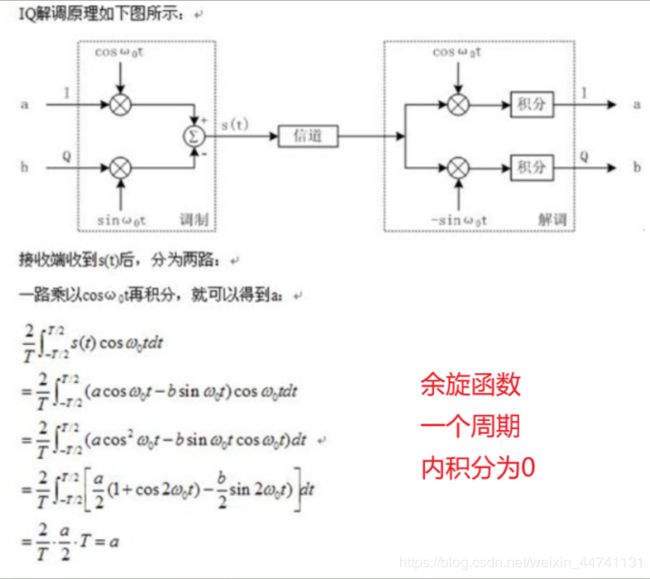
这个就是IQ调制和解调的原理，然后就是如何应用IQ调制来实现MPSK调制（QPSK、8PSK等）、MQAM调制（16QAM、64QAM等）了。
BPSK(二相相移位键控)：


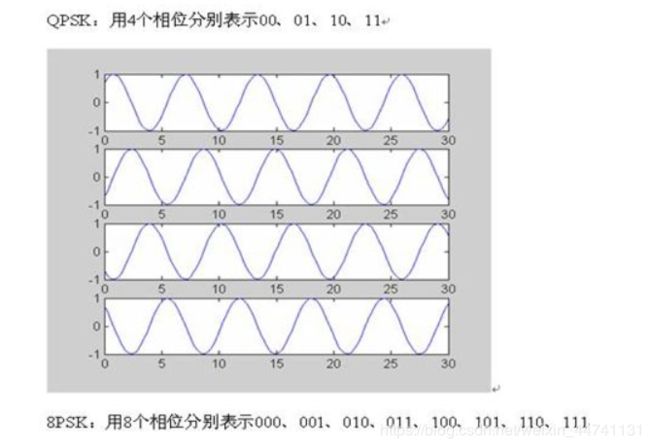
也就是用载波的相位来调制基带信号。然后MPSK就是通过IQ调制得到不同的相位来表示符号。比较简单就不继续写啦。

使用IQ调制实现QAM调制

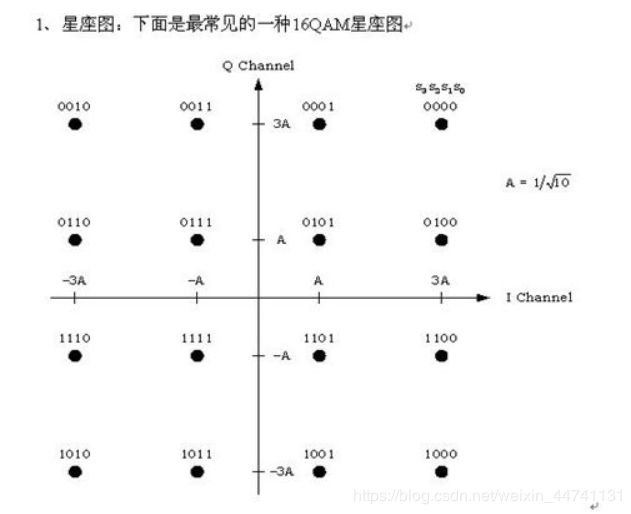
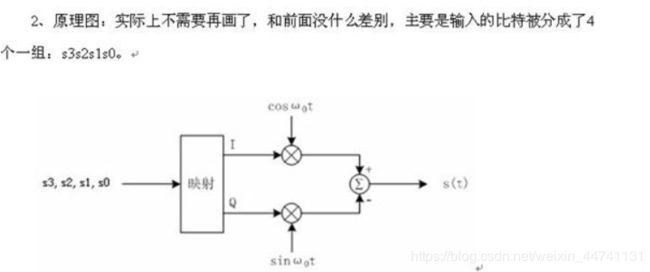
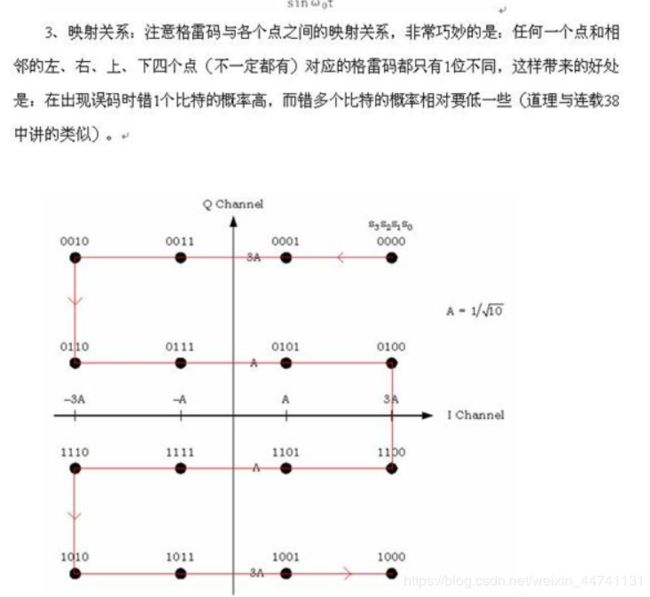
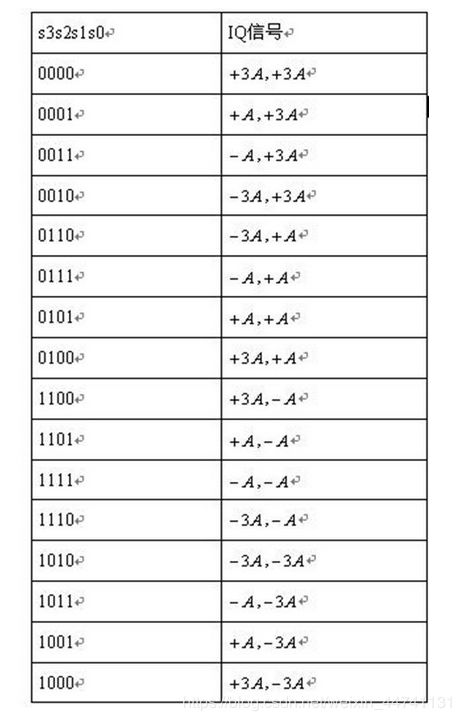
星座图解释：星座图，就是说一个坐标，如单位圆，横坐标是I，纵坐标是Q，相应于投影到I轴的，叫同相分量，同理投影到Q轴的叫正交分量。由于信号幅度有差别，那么就有可能落在单位圆之内。具体地说，64QAM，符号有64个，等于2的6次方，因此每个符号需要6个二进制来代表才够用。这64个符号就落在单位圆内，根据幅度和相位的不同 落的地方也不同。从其中一个点跳到另一个点，就意味着相位调制和幅度调制同时完成了。”
调制中用格雷码原因：为了减少误判比特，解调出的值按汉明距离来判断是哪个码，如果错了格雷码上下左右也才差一个比特。

多载波调制和DFT

进行IFFT计算时， IFFT的运算过程是纯数学运算，必须认为的赋予数据物理意义。输入的数据是频域信息，每一个数据代表了对应频点上的采样值，输入数据的数量代表了以采样频率权值的频域采样值，假设输入数据的数量为n，每两个数据之间的频率间隔为f，则采样速率为nf，也就是说输入数据是在带宽为nf范围内的均匀采样值。输出的数据是时域信息，假设OFDM每一个符号时间为T，IFFT输出数据的数量为n,那么输出数据的采样频率即为n/T，根据奈奎斯特采样定理，如果信号的带宽为f1，那么如果要准确表达被采样信号的频域信息，采样速率至少为2f1。(结合数字信号时域频域采样的知识)

保护间隔和循环前缀

为了最大限度地消除符号间干扰，还可以在每个OFDM符号之间插入保护间隔，而且保护间隔长度Tg一般要大于无线信道中的最大时延，这样一个符号就不会对下一个符号造成干扰。再这段保护间隔内可以不插入任何信号，即是一段空白的传输时段，然而在这种情况下，由于多径传播的影响，接收端实现同步有一定困难。

帮助理解：信号可以在多条路径上传播而先后到达接收端，多经效应造成了了OFDM符号间的干扰(ISI)，所以需要在OFDM符号之前留出一段保护时间(Guard time)，又叫前缀(Prefix)，其时间宽度大于信道的最大时延扩展(delay spread)。这样前一个符号的多个时延信号完全被前缀吸收，不会影响后一个符号。如果采用全零前缀，只能消除符号间的ISI，却不能消除符号内部的码间干扰（ICI）。为了解决上述问题，在实际系统中使用OFDM符号的周期扩展作为循环嵌缀，将OFDM符号的最后一段的时域信号的拷贝插入到保护时间当中。(还是很没有理解保护间隔是如何保护)

为了便于同步，人们又在OFDM符号的保护间隔内填入循环前缀信号，即将每个OFDM符号后的Tg时间中的样点复制到OFDM符号的前面，形成前缀，在交接点没有任何的间断，下图显示了循环前缀的插入

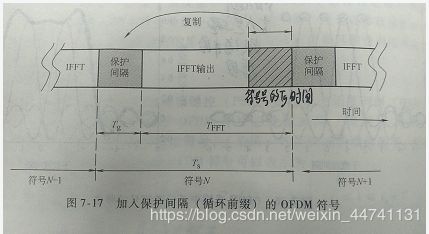
循环前缀CP的引入，使得OFDM传输在一定条件下可以完全消除由于多径传播造成的符号间干扰（ISI）和子信道间干扰（ICI）的影响，大大推进了OFDM技术实用化的进程。
注意：OFDM“符号”（symbol）是一个容易产生歧义的概念。在多数OFDM 文献中，OFDM“符号”指的是调制信息序列X（N）（IFFT输出的时域抽样序列），而X（N）的各分量（即各子载波上的调制信息）也用“符号”（symbol）表示。为避免这种混乱，我们将X（N）连同循环前缀称为OFDM“帧符号”，简称“符号”，称的分量为“帧内符号”。OFDM 文献中的符号间干扰（ISI）指的是帧符号间的干扰，具体是指除去循环前缀后的帧符号间的干扰，同样符号同步也是指帧符号同步。
好了，这个就是OFDM我所了解的调制过程吧，然后下面就是有一些疑惑点的补充。

OFDM频谱和功率谱

频谱

上面的多载波调制和FFT的公式1.2.2忽略了矩形函数（当基带信号为矩形脉冲表示时，一个码元宽度）。即可以表示如下：

所以，时域上每个OFDM信号X(K)与脉冲宽度为T的矩形脉冲相乘，频域上时对应频谱的卷积，即Sa(fT)函数与一组位于各个子载波频率上的δ函数的卷积，即相当于把Sa(fT)的中心频率搬移到δ函数的频率上。卷积结果如图所示：


当所有载波组合在一起时，总的频谱非常接近与矩形频谱，看上面确实长的像对不。与其它多载波调制方案相比，OFDM信号载波之间的正交性，可以避免载波间干扰(ICI)，具有更高频带利用率。

所以假设采样频率为fs，OFDM符号长度为Ts，子载波频率为fk
若基带信号采用矩形信号，则每个子信道已调信号频谱为Sa(x)形状，主花瓣宽度为2/Ts
所以他们关系为：
由前面IFFT调制那得到fk=k*fs/N
且采样频率fs=N/Ts
采样周期T=N/Ts
由这里知相邻子载波间隔为Δf=fs/N=1/Ts
所以注意对比相邻子载波间隔Δf和Sa(x)形状，主花瓣宽度为2/Ts就可以看出前面频谱的关系啦。

功率谱

OFDM符号的功率谱密度为N个子载波上的信号的功率谱密度之和。


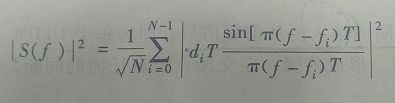
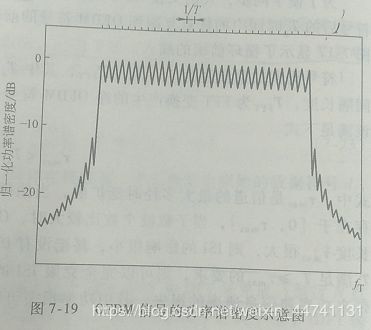
这是N=32的OFDM功率谱密度图。纵坐标为归一化功率谱密度，单位dB，很坐标为归一化频率ft。

正交的理解

sin(t)和sin(2t)是正交的【因为：sin(t)·sin(2t)在区间[0,2π]上的积分为0】
在下面的图示中，在[0,2π]的时长内，采用最易懂的幅度调制方式传送信号：sin(t)传送信号a，因此发送a·sin(t)，sin(2t)传送信号b，因此发送b·sin(2t)。其中，sin(t)和sin(2t)的用处是用来承载信号，是收发端预先规定好的信息，称为子载波；调制在子载波上的幅度信号a和b，才是需要发送的信息。因此在信道中传送的信号为a·sin(t)+b·sin(2t)。在接收端，分别对接收到的信号作关于sin(t)和sin(2t)的积分检测，就可以得到a和b了。（和IQ调制那一样）
再下一步，将cos(t)也引入。容易证明，cos(t)与sin(t)是正交的，也与整个sin(kt)的正交族相正交。同样，cos(kt)也与整个sin(kt)的正交族相正交。因此发射序列扩展到{sin(2π·Δf·t),sin(2π·Δf·2t),sin(2π·Δf·3t),…,sin(2π·Δf·kt),cos(2π·Δf·t),cos(2π·Δf·2t),cos(2π·Δf·3t),…,cos(2π·Δf·kt)}
所以咧，上面的多载波调制和FFT的公式1.2.2可以看出s(t)的实部和虚部分别对应于符号的同相和正交分量，通过IFFT就可以让X(t)调制实现。

总结

就这样吧，虽然还有好些东西没有搞懂和写上，但是总的来说应该达到我想要的了，不够再补充。害，准备期末去了。
留下的问题:

• 循环前缀cp实现他的作用原理

参考

OFDM调制解调
OFDM的基本原理
这两个文档都有下载到
给"小白"图示讲解OFDM的原理

无线通信中的IQ调制，BPSK调制，QPSK调制，16QAM调制的理解