手推机器学习系列笔记——手推SVM(2) 对偶问题探讨、Slater条件、核技巧、SMO算法推导+简单实现代码、数据集
一、两个问题
在我的上一篇博客手推SVM(1)中有两个问题值得探讨:(传送门:https://blog.csdn.net/Fox_Alex/article/details/105113554)
- 为什么转对偶?是否所有的都可以转对偶?何时转对偶?
- Slater条件
通过查阅大量文献、博客、视频教程,就目前我对这两个问题的认识如下,希望能和大家一起探讨探讨:
解答:
问题1:转对偶
对偶性在我的上一篇博客手推SVM(1)已做了几何解释和证明,需要的话去看呀~
(传送门:https://blog.csdn.net/Fox_Alex/article/details/105113554)
- 对偶问题可以理解为同一问题的另一个方面; 相对来说化难为易(把难以求解的约束条件扔到目标函数的位置上去),如果问题的形式合适(变量少,约束多)还可以通过把约束变量和对偶变量互换来把大规模问题转换成小规模问题;
- 一般性,对所有实数域上的优化问题都有其对偶问题;(需要探讨)
- 弱对偶定理给原问题的最优解定了一个下界,弱对偶是一定存在的(在手推SVM(1)中已证),强对偶定理给出了原问题最优解的一个解; 对于非凸问题或者整数规划问题,尽管不再有强对偶定理,但是通过弱对偶定理往往可以得到对原问题的一个下界(lower bound),这对于我们求解原问题有时会有非常大的增益;
参考:https://www.zhihu.com/question/43830699/answer/110807943
问题2:Slater条件
- Slater条件的理解:Slater条件总结起来就是让该凸优化问题存在绝对可行域(存在一个相对内部的点x,使得所有的不等式约束均成立[补充:等式约束可以转换为两个不等式约束]),那么就具有强对偶性。Slater条件建立了“使原问题有解”的约束条件
- Slater条件的证明:
详见:https://blog.csdn.net/u010510549/article/details/100938214
更详细见:Convex Optimization by Boyd and Vandenberghe. P234. Section 5.3.2
二、 核技巧
核技巧有一部分内容在手推SVM(1)中已经叙述过了,下面主要从另外一个角度(从简化运算的角度)来讲为什么使用核技巧。内容主要参考林轩田老师的《机器学习技法》,学过之后深思良久,老师站的角度很给人启发!
补充:核技巧的使用一定程度上增加了模型复杂度,正则化的使用会减少模型复杂度。
(提示:这个总结并没有结束哦,下一张图还有一部分~)
高斯核虽然比较流行和常用,但是使用要非常非常小心,参数选择不当会过拟合(上图的第三个分类结果可见)!!!
我总结的核技巧的本质是用一种相对较少的计算量来计算向量在Z空间的相似性。并非所有的相似性计算方法都是核方法,还需满足Mercer's Condition,证明过程详见《统计学习方法》,必要性是显然的,充分性需要借助泛函理论(尤其是核的再生性和再生核的希尔伯特空间,这个理论真的太牛逼了!!!大赞~)什么是希尔伯特空间,参考我上一篇博客,手推SVM(1)。
三、SMO算法推导
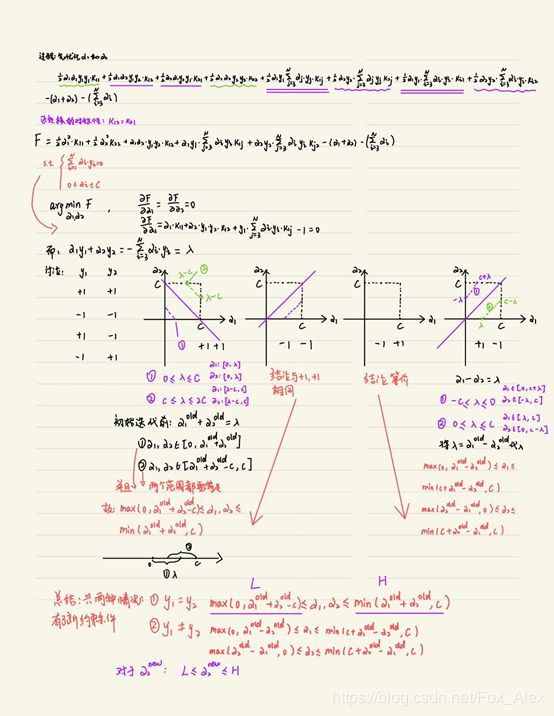
SMO算法的求解过程相对来说,比较繁琐,思想类似坐标上升法。下面是详细推导过程:
另外还需特别注意的是变量![]() 和
和![]() 的选择以及更新完后对b和Ei的更新。
的选择以及更新完后对b和Ei的更新。
四、SMO简单实现代码
python3.7 + numpy1.16.5 + matplotlib3.1.1
test.py文件:
from helper import *
from simpleSMO import *
import time
filename = "D:/Code/ML/SVM/testSet.txt"#替换成自己的数据集路径哦
dataMat1,labelMat1=loadDataSet(filename)
start=time.time()
#b1,alphas1=SMOsimple(dataMat1,labelMat1,0.5,0.001,100)
b1,alphas1=Simple_SMO(dataMat1,labelMat1,0.5,100)
print ("\n","time used:.{0}s".format(time.time()-start))
w1=weight(dataMat1,labelMat1,alphas1)
#print(w1)
plotBestFit(w1,b1,filename)helper.py文件:
import numpy as np
import matplotlib.pyplot as plt
def loadDataSet(filename):
#filename是待读取文件的文件名或路径+文件名
dataMat = []
labelMat = []
fr = open(filename)
for line in fr.readlines():
lineArr = line.strip().split("\t")
dataMat.append([float(lineArr[0]), float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat,labelMat
def randPickj(i,m):
#i是alphai的i值,整数; m是alpha个数; j不能等于i
j = i
while j == i:
j = int(np.random.uniform(0,m))
return j
def clipAlpha(aj,H,L):
#使选择的点在[L,H]范围内,目的为了满足KKT条件
if aj>H:
aj=H
if aj0:
w+=labelMatrix[i]*alphas[i]*dataMatrix[i,:]
return w.tolist()
def plotBestFit(weights,b,filename):
dataMat,labelMat=loadDataSet(filename) #加载样本特征、样本类别
dataArr=np.array(dataMat)
n=dataArr.shape[0] #n个样本
xcord1=[];ycord1=[]
xcord2=[];ycord2=[] #两个类别的样本的xy坐标值,x对应x1,y对应x2
#将样本数据根据样本类别标签labelMat分别放入不同的坐标集中
for i in range(n):
if int(labelMat[i])==1: #第i个样本是1类
xcord1.append(dataArr[i,0]) #第i个样本的x1值
ycord1.append(dataArr[i,1]) #第i个样本的x2值
else:
xcord2.append(dataArr[i,0]) #第i个样本的x1值
ycord2.append(dataArr[i,1]) #第i个样本的x2值
#绘制两类样本的散点图
fig=plt.figure(figsize=(12,8))
plt.scatter(xcord1,ycord1,c="red",s=50,label="label=1")
plt.scatter(xcord2,ycord2,c="blue",s=50,label="label=-1") #继续在原图上作图
#绘制决策边界
x=np.arange(-3.0,5.0,0.1)
y=(-b-weights[0][0]*x)/weights[0][1] #由w1*x1+w2*x2+b=0得到x2(即y)=(-b-w1x1)/w2
x.shape=(len(x),1);y.shape=(len(x),1)
plt.plot(x,y,color="darkorange",linewidth=3.0,label="Boarder") #继续在ax图上作图
plt.xlabel("X1",fontsize=16)
plt.ylabel("X2",fontsize=16)
plt.title("SMO BestFit",fontsize=20,fontweight="bold")
plt.legend() #添加图标注解
plt.show() simpleSMO.py文件:
from helper import *
def Simple_SMO(dataset, labels, C, max_iter):
'''
C:软间隔常数
max_iter:外层循环最大迭代次数
'''
dataset = np.array(dataset)
m, n = dataset.shape
labels = np.array(labels)
alphas = np.zeros(m)
b = 0
it = 0
def f(x):
"分类器函数:y = w^T * x + b"
x = np.matrix(x).T
data = np.matrix(dataset)
ks = data * x
wx = np.matrix(alphas * labels) *ks
fx = wx + b
return fx[0, 0]
while it < max_iter:
pair_changed = 0
for i in range(m):
a_i, x_i, y_i = alphas[i], dataset[i], labels[i]
fx_i = f(x_i)
E_i = fx_i - y_i
j = randPickj(i, m)
a_j, x_j, y_j = alphas[j], dataset[j], labels[j]
fx_j = f(x_j)
E_j = fx_j - y_j
K_ii, K_jj, K_ij = np.dot(x_i, x_i), np.dot(x_j, x_j), np.dot(x_i, x_j)
eta = K_ii + K_jj - 2*K_ij
if eta <= 0:
print('WARNING eta <= 0')
continue
# 获取更新的alpha对
a_i_old, a_j_old = a_i, a_j
a_j_new = a_j_old + y_j*(E_i - E_j)/eta
# 对alpha进行修剪
if y_i != y_j:
L = max(0, a_j_old - a_i_old)
H = min(C, C + a_j_old - a_i_old)
else:
L = max(0, a_i_old + a_j_old - C)
H = min(C, a_j_old + a_i_old)
a_j_new = clipAlpha(a_j_new, H, L)
a_i_new = a_i_old + y_i*y_j*(a_j_old - a_j_new)
if abs(a_j_new - a_j_old) < 0.00001:
#print('WARNING alpha_j not moving enough')
continue
alphas[i], alphas[j] = a_i_new, a_j_new
# 更新阈值b
b_i = -E_i - y_i*K_ii*(a_i_new - a_i_old) - y_j*K_ij*(a_j_new - a_j_old) + b
b_j = -E_j - y_i*K_ij*(a_i_new - a_i_old) - y_j*K_jj*(a_j_new - a_j_old) + b
if 0 < a_i_new < C:
b = b_i
elif 0 < a_j_new < C:
b = b_j
else:
b = (b_i + b_j)/2
pair_changed += 1
print('INFO iteration:{} i:{} pair_changed:{}'.format(it, i, pair_changed))
if pair_changed == 0:
it += 1
else:
it = 0
print('iteration number: {}'.format(it))
return b, alphas运行结果图:(对100个样本进行分类)
部分代码也参考了一些优秀的博主的工作,后期我会添加参加文献~另外数据集文件和代码打包后已经放到资源里了哦~大家自行下载。
写到这里,SVM的部分就全部结束了,撒花❀❀❀机器学习真的是博大精深,学习和推导精巧的机器学习理论、算法并付诸于实践真的是一件非常有趣的事情呢,推导的每一项设计都那么精细和巧妙,为前人的智慧所倾倒,尤其是那些研究优化理论的大师们,真的tql!!!算法的精巧让我们这些研究计算机科学的人沉醉其中,这是最原始和最纯粹的快乐呀~新的篇章马上开启,大家敬请期待~~~