线性支持向量机中KKT条件的讨论

线性支持向量机中KKT条件的讨论

此处的模型为训练样本不可分时的线性支持向量机，简称为线性支持向量机。即考虑松弛变量 ξi 和惩罚参数 C ，目标函数为

12∥w∥2+C∑i=1Nξi

原始问题

则线性不可分的线性支持向量机的学习问题变成如下的凸二次规划（convex quadratic programming）问题，即原始问题

minw,b,ξs.t.12∥w∥2+C∑i=1Nξiyi(w⋅xi+b)≥1−ξi,i=1,2,⋯,Nξi≥0,i=1,2,⋯,N

对偶问题

原始问题的拉格朗日函数为

L(w,b,ξ,α,μ)=12∥w∥2+C∑i=1Nξi−∑i=1Nαi(yi(w⋅xi+b)−1+ξi)−∑i=1Nμiξi

对偶问题拉格朗日函数的极大极小问题，得到以下等价优化问题

minαs.t.12∑i=1N∑j=1Nαiαjyiyj(xi⋅xj)−∑i=1Nαi∑i=1Nαiyi=00≤αi≤C,i=1,2,⋯,N

KKT条件

原始问题的解对偶问题的解相同需要满足KKT对偶互补条件，即

αi(yi(w⋅xi+b)−1+ξi)=0μiξi=0(1)(2)

对样本 xi ，记SVM的输出结果为

ui=w⋅xi+b

Platt在序列最小优化（SMO）方法 1中提到，对正定二次优化问题（a positive definite QP problem）的优化点的充分必要条件为KKT条件（Karush-Kuhn-Tucker conditions）。
对于所有的 i ，若满足以下条件，QP问题可解。

αi=0⇔yiui≥10<αi<C⇔yiui=1αi=C⇔yiui≤1(3)(4)(5)

其中 yiui 就是每个样本点的 函数间隔，分离超平面 (w,b) 对应的函数间隔 γ̂  取为1.

KKT条件的推导

下面我们将要讨论如何从式(1)、(2)得到式(3) ~ (5)。

(1) αi=0

由 C−αi−μi=0 ，得

μi=C

则由式(2)可知，

ξi=0

再由原始问题的约束条件 yi(w⋅xi+b)≥1−ξi ，有

yiui≥1

(2) 0<αi<C

将 μi 乘到式(1)，有

μiαiyiui−μiαi+μiαiξi=0μiαi(yiui−1)=0

又 C−αi−μi=0 ，则

(C−αi)αi(yiui−1)=0

因为 0<αi<C ，所以

yiui=1

又由式(1)，有

yiui=1−ξi⇒ξi=0

(3) αi=C
由式(1)，有

yiui−1+ξi=0yiui=1−ξi(6)

因为 ξi≥0 ，所以

yiui≤1

即可得式(3) ~ (5)，KKT条件得以推导。

KKT条件的几何解释

在线性不可分的情况下，将对偶问题的解 α∗=(α∗1,α∗2,⋯,α∗N)T 中对应于 α∗i>0 的样本点 (xi,yi) 称为支持向量2。
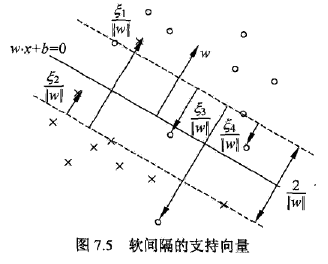
如下图所示，分离超平面由实线表示，间隔用虚线表示，正例由“o”表示，负例由“x”表示。实例 xi 到间隔边界的距离为 ξi∥w∥ 。

软间隔的支持向量 xi 或者在间隔边界上，或者在间隔边界与分离超平面之间，或者在分离超平面误分一侧。
这里可以从两种角度来解释，第一种角度就像李航在《统计学习方法》第113页中用到间隔边界的距离边界 ξi∥w∥ 。因为， 1−ξi∥w∥ 为样本点 xi 到分类超平面的距离， 1∥w∥ 是分类间隔到分类超平面的距离，可以根据 ξi 的大小来判断分类情况。

若 α∗i<C ，则 ξi=0 ，支持向量 xi 恰好落在间隔边界上；
若 α∗i=C,0<ξi<1 ，则分类正确， xi 在间隔边界与分离超平面之间；
若 α∗i=C,ξi=1 ，则 xi 在分离超平面上；
若 α∗i=C,ξi>1 ，则 xi 位于分离超平面误分一侧。

现在我们要从另外一种角度，也就是KKT条件（式(3)~(5)），通过数学推导来得到上面的结果。

在间隔边界上

由式(3)可知，当 0<α∗i<C 时， yiui=1 ，则分类正确，且 ui=±1 ，即在分类间隔边界上。

在间隔边界与分离超平面之间

当 α∗i=C,0<ξi<1 时，由式(6)得

0<yiui<1

则说明 yi,ui 同号，分类正确，且函数间隔小于1，即在间隔边界内。

在分离超平面上

当 α∗i=C,ξi=1 时，由式(6)得

yiui=0⇒ui=0

即 xi 在分离超平面上。

在分离超平面误分一侧

当 α∗i=C,ξi>1 时，由式(6)得

yiui<0

则分类错误， xi 在分离超平面误分的一侧。

以上就是对线性支持向量机中KKT条件的仔细讨论，从公式推导和几何意义上一同解释了为什么 α∗i 与 C 的大小关系决定支持向量的位置。
这是我在看书的时候不是很明白的问题，现在通过理论上的推导能够清楚地得到结果，也希望能够解答其他有同样问题人的疑惑。

问题是越思考越清楚，希望在今后的学习中继续保持这种认真对待知识的态度。

---

1. Platt J. Sequential minimal optimization: A fast algorithm for training support vector machines[J]. 1998. ↩
2. 李航. 统计学习方法[J]. 清华大学出版社, 北京, 2012. ↩