【论文阅读】RegNet-Designing Network Design Space
文章目录
- 1. 动机
- 2. 方法
- 2.1 网络基本结构
- 2.2 从AnyNetA到AnyNetE
- 2.3 RegNet
- 3. 总结
- 4. 没有理解透的点
1. 动机
当前设计网络结构的方法大部分是基于手工的,即通过做实验来确定相对最优的网结构。如果网络结构比较复杂,需要调整的超参数较多,手工的方式就很难找到最优的网络结构。所以大佬们设计了NAS(Network Architecture Search)及其拓展的方法,让网络自己去搜索最优的结构。其发展历程可以参考知乎CLAY的回答。本文表示NAS的搜索结果只是针对单一的网络实例,不具有一般性,无法直接迁移到其他的网络或者任务上。这篇文章不仅提出了一个新的网络结构,还从构建这个网络结构的流程上,总结出了一些可以通用的网络结构设计原则,相当于半自动化的NAS。
2. 方法
2.1 网络基本结构
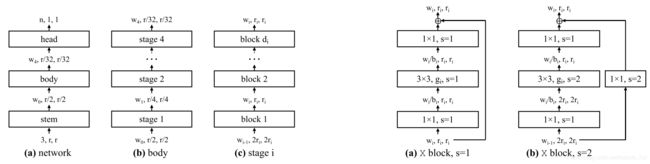
其中整个网络分成三个部分:stem->body->head,其中输入图片是224x224x3,stem部分是一个卷积层,卷积核为3x3,卷积核数量为32,strides=2。head则是全连接层,用于输出n个类别。
而body部分由4个stage组成,从stage1到stage4,分辨率逐次减半,但是每一个stage输出的特征图的数量w1,w2,w3,w4则作为超参数需要用到本文所提到的方法去搜寻;
每一个stage又是由 d i d_i di个相同的block构成,本文大部分实验所使用的block都是residual bottleneck block,如上图中最右边的图所示。其中block的数量 d i d_i di也作为超参数需要搜寻确定。
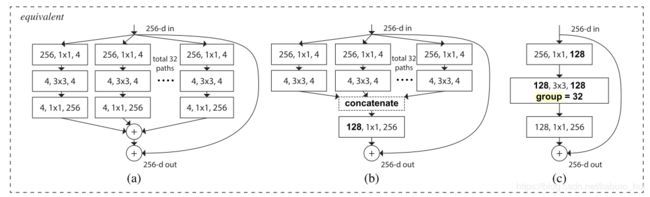
在residual bottleneck block中,存在3个参数:block最终输出的特征图数量(width) w i w_i wi;bottleneck ratio b i b_i bi(用于确定block内部的特征图数量);group width g i g_i gi(与Inception结构类似,block横向重复的数量,如下如所示):
综上所述,网络有4个stage,每个stage中需要搜寻确定的参数有block的数量 d i d_i di;block width w i w_i wi;bottleneck ratio b i b_i bi;group width g i g_i gi;共计16个参数(文章中称为16个自由度)。找到这16个参数的最优设置,就是本文所完成的工作。
2.2 从AnyNetA到AnyNetE
文章首先确定了参数的取值范围:
| Type | Abbrev | Range |
|---|---|---|
| width | w i w_i wi | ≤ \leq ≤ 1024 (可以被8整除) |
| depth | d i d_i di | ≤ \leq ≤ 16 |
| bottleneck ratio | b i b_i bi | {1, 2, 4} |
| group width | g i g_i gi | {1,2,…,32} |
这就是初始的Design Space,也就是AnyNetA的解空间。如果采用穷举的方式,那么将会有 ( 6 x 128 x 3 x 6 ) 4 (6x128x3x6)^4 (6x128x3x6)4,大约 1 0 18 10^{18} 1018这么多种可能。所以作者采用了一种抽样的方式,有放回的从Design Space中取出500个模型(每个模型的flops在360MF-400MF之间),每个模型只训练10 epochs。所谓抽取模型,其实就是通过对数均匀采样(log-uniform)【尚未理解其原理】的方式从上述的取值范围中提取出网络关键参数。最后根据误差经验分布公式error Empirical Distribution Function(EDF)来判断该设计空间的质量:
F ( e ) = 1 n ∑ i = 1 n l [ e i < e ] F(e) = \frac{1}{n}\sum_{i=1}^{n}l[e_i < e] F(e)=n1i=1∑nl[ei<e]
即抽样模型中满足误差要求的模型所占的比例。
固定所有stage中bottleneck ratio b i b_i bi 为一个定值,这样得到的Design Space称为AnyNetB。【结果表明,共享bottleneck ratio时,模型的精度没有损失】。
于是在B的基础上,进一步的共享group width g i g_i gi 为一个定值,得到Design Space称为AnyNetC。【结果表明,共享参数group width时,模型的精度没有损失】。
在C的基础上发现那些当前最优的模型所具有的一个共性是其网络结构具有递增的通道数(widths)。所以添加规则 w i + 1 > = w i w_{i+1} >= w_i wi+1>=wi, 得到Design Space称为AnyNetD。【结果表明递增widths,性能提升】。
在D的基础上发现当网络性能随着stage width的增加而增加时,depth也有同样的趋势,于是添加规则 d i + 1 > = d i d_{i+1} >= d_i di+1>=di, 得到Design Space称为AnyNetE。【结果表明递增depths,性能提升】。
2.3 RegNet
在AnyNetD和AnyNetE的基础上,作者发现block输出特征图数量(width)与block的index呈线性关系,所以引进了一个block width计算公式:
u j = w 0 + w a ∗ j ( 0 ≤ j < d ) u_j = w_0 + w_a* j \ \ (0 \leq j < d) uj=w0+wa∗j (0≤j<d)
其中 w 0 w_0 w0是初始width, w a w_a wa是斜率, u j u_j uj是计算后得到的block j的width。
然后根据下面的式子为每个block j计算 s j s_j sj :
u j = w 0 ∗ w m s j u_j = w_0 * w_{m}^{s_j} uj=w0∗wmsj
s j = l o g w m u j w 0 s_j = log_{w_m} \frac{u_j}{w_0} sj=logwmw0uj
为了量化 u j u_j uj ,将上述计算得到的 s j s_j sj 进行简单的四舍五入,利用下面的式子就可以得到每个block的量化(quantized)width w j w_j wj :
w j = w 0 ∗ w m ⌊ s j ⌉ w_j = w_0 * w_{m}^{\left\lfloor {s_j} \right\rceil} wj=w0∗wm⌊sj⌉
因此,这里又多了3个参数: w 0 w_0 w0 , w a w_a wa, w m w_m wm ; 给定一个模型,固定网络深度depth参数d,然后采用网格搜索的方式最小化预测与实际的每个block width的平均对率比,这里写作 e f i t e_{fit} efit,没有具体公式,可以大胆推测一下为:
e f i t = 1 n ∑ j = 1 n l o g w ^ j w j e_{fit} = \frac{1}{n} \sum_{j=1}^{n}log\frac{\hat w_j}{w_j} efit=n1j=1∑nlogwjw^j
这种线性参数化(linear parametrization)自然的给 w i w_i wi 和 d i d_i di 添加了一种递增的约束,符合AnyNetE中的观测结果的。
通过上面的分析,进一步的将设计空间限制到6个维度:d, w 0 w_0 w0 , w a w_a wa, w m w_m wm , b, g,把从这种Design Space中找到的网络结构称为RegNet ,其参数限制为:
| Type | Abbrev | Range |
|---|---|---|
| depth | d d d | < 64 |
| initial width | w 0 w_0 w0 | < 256 |
| slope | w a w_a wa | < 256 |
| - | w m w_m wm | [1.5, 3] |
| bottleneck ratio | b b b | {1, 2, 4} |
| group width | g g g | {1,2,…,32} |
其中b,g基于AnyNetXE上的$e_{fit} $来确定范围。
综上所述,从AnyNetA到RegNet实际上是通过抽样、统计的方式,找到能使模型性能提升的规则,然后添加这些规则并逐步缩小Design Space的过程。从下面的表也能看出:
文章在RegNetX的基础上添加了Squeeze-and-Excitation(SE)操作,得到的设计空间称为RegNetY。SE操作类似于gate操作,加权:
当然文章也探讨更多的情况,比如3stages或者5stages,使用不同的block等,基于这些原则都能搜寻到更好的network。
3. 总结
本文提出了一种半自动化的最优网络结构搜寻方法,通过不断添加规则缩小Design Space,从而找到较优的网络结构。文章中所发现的一些网络结构构造的原则,有的符合我们的经验,有的与我们经验正好相反,还有一些我们之前没有关注到的一些方面。
一致的经验:
- good network have increasing widths.
相反的经验:
- 网络并不是越深越好,实验表明最佳的模型大约20个blocks(60层左右)。
- bottleneck并没有对性能提示没有太大帮助(文中观点,实验表示b=1时最好,b<1(inverse bottleneck)则更糟)。
- width并没有随着stage的增加而增加两倍,大约是2.5倍时最好(文中实验证明)。
没有关注到的点:
- stage width w i w_i wi 和stage depth d i d_i di 都随着i的增加而增加,最后一个stage可能不满足此规律(对于4个stage的模型来说,一般stage3 block最多,stage4 block最少)。
- 想要获取较好的runtime,建模的时候activations和flops最好基于平方根和线性关系。
此外,文中还提及到两个激活函数relu和swish,其中swish表达式为:
f ( x ) = x ∗ s i g m o i d ( β x ) f(x) = x * sigmoid(\beta x) f(x)=x∗sigmoid(βx)
根据实验,relu适用与high-flops的模型,swish适用于low-flops的模型。个人认为是在high-flops的模型中,计算swish比计算relu要慢很多。
4. 没有理解透的点
1.对数均匀采样(log-uniform sampling)的原理是什么?怎么采?
2.width量化那块的公式(3)来的太突兀,不是很理解。
欢迎大家讨论~