机器学习——支持向量机SVM（Support Vector Machine）（上）

1、概述

最早是在1963年由Vladimir N.Vapmik和Alexey Ya.Chervonenkis提出的，目前的版本（soft margin）在1993年是由Cormna Cortes和Vapnik提出的并在1995年发表。在2012年深度学习出现之前，SVM被认为是近十几年来表现最好和最成功的算法。

SVM（Support Vector Machine）——在机器学习领域，是一个有监督的学习模型，通常用来进行模式识别、分类以及回归分析。

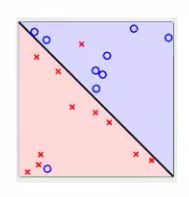
举例：下图中有所少条直线可以将两类点区分开？哪条是最好的？

即：可以将两类点区分开的直线有无数条，最好的那条就是今天要说的SVM的目标。

2、SVM的目标

寻找可以区分两类点的超平面（hyper plane），使得边际（margin）最大，此时区分两类点出现的错误几率是最小的。

边际（margin）的定义：超平面到两类点最近的距离

在下图中，如何选取使margin最大的超平面（Max Margin Hyperplane）?

选取边际最大的超平面的方法：超平面到一侧最近点的距离等于到另一侧最近点的距离，与两侧的两个超平面平行。

3、线性可区分（linear separable）和线性不可区分（linear inseparable）

上面两个图都是线性不可区分对的例子。

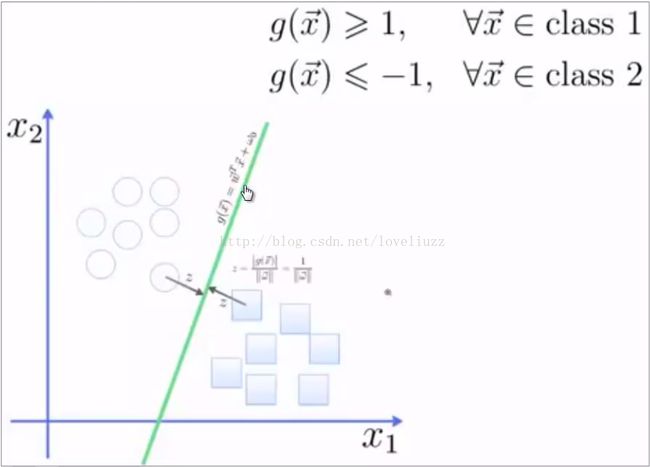
4、超平面的定义与公式推导：

超平面可以定义为：，其中，，W：权重向量（weight vector）（1*n维）

n：特征值的个数，X：训练示例（n*1维），b：偏好（bias）

假设2维的特征向量：X = {X1，X2}，则W = {W1，W2}，将b看成是额外的weight（W0），

超平面方程变为：，则超平面右上方的点满足：

超平面左下方的点满足：

调整W，使得超平面定义的边际的两边为：

综合两式得到：

结论：所有落在边际两边的超平面上的点被称作“支持向量”

经过公式的推导，可得出结论：分界的超平面H和两边的超平面H1或H2上面的任意一点的距离为：

其中，是向量的范数（norm），范数定义为：。

所以，最大的边际距离（margin）为：

5、求解最大边际的超平面

利用KKT条件和拉格朗日公式，可以变为有限制的凸优化问题，推导结论为：

其中，是支持向量点的类别标记，公式只是对支持向量点进行求和；：要测试的示例；

和都是单一数值型参数，由算法得出，是支持向量点的个数。

最后，将任何测试示例带入到公式里面，归类由得出符号的正负来决定。

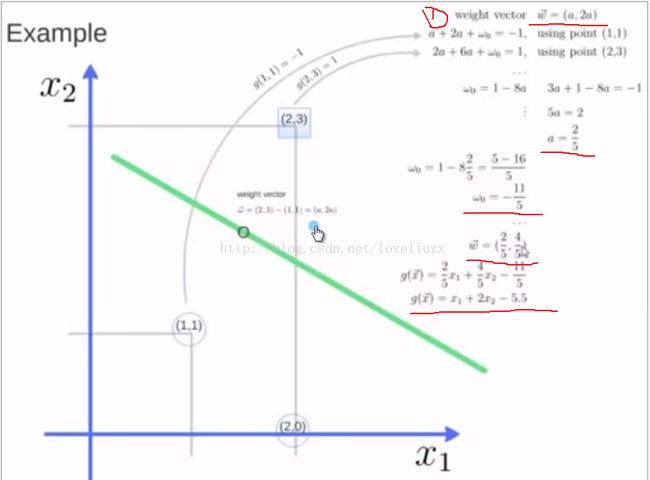
6、举例：已知3个点（1,1） (2,3) (2,0)，求解最大边际的超平面？

对上述例子用Python语言在PyCharm中实验运行一下：

#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author:ZhengzhengLiu

from sklearn import svm         #from 库名 import 模块
X = [[2,0],[1,1],[2,3]]         #X：数据特征向量,包含3个示例,在Python中用列表（list）表示
y = [0,0,1]                     #y：数据对应的分类标记,Python中常用0,1定义两类问题
clf = svm.SVC(kernel='linear') #clf:创建的分类器对象,导入svm的SVC类（支持向量分类）采用线性的核函数
clf.fit(X,y)                   #用训练数据拟合分类器模型

print(clf)                     #打印分类器的内容
print(clf.support_vectors_)    #打印支持向量
print(clf.support_)            #打印支持向量的下标/索引
print(clf.n_support_)          #打印对于每一个类中支持向量的个数
print(clf.predict([0,4]))      #用训练好的分类器去预测[0,4]数据的分类标记

运行结果为：

SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
  decision_function_shape=None, degree=3, gamma='auto', kernel='linear',
  max_iter=-1, probability=False, random_state=None, shrinking=True,
  tol=0.001, verbose=False)
[[ 1.  1.]
[ 2.  3.]]
[1 2]
[1 1]
[1]

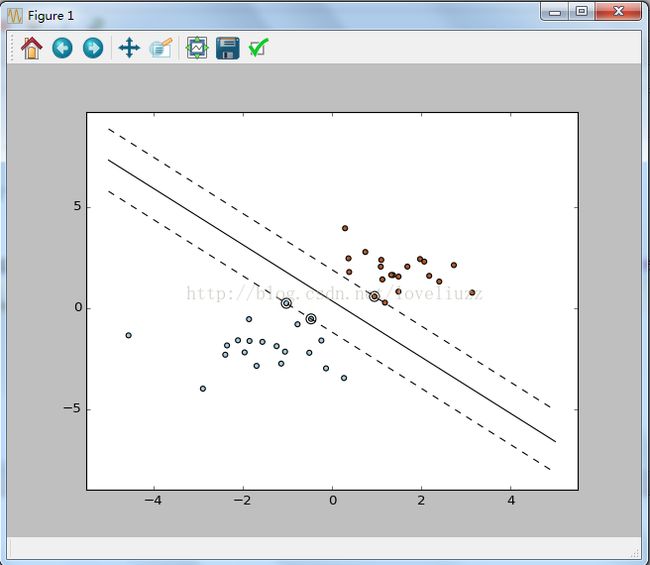
示例2：随机生成的40个点（线性可分情况）进行二分类，绘制所有的点以及支持向量点，并画出超平面以及与支持向量点相切的超平面。

#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author:ZhengzhengLiu

print(__doc__)
import numpy as np    #导入numpy模块（支持矩阵运算）并命名为np
import pylab as pl    #导入pylab模块（画图功能）并命名为pl
from sklearn import svm

#创建40个孤立的点(属于线性可区分的情况)

#random:随机函数,调用.seed方法，0表示随机抓取的值是固定不变的
np.random.seed(0)
#numpy.r_是将一系列的序列合并到一个数组中，调用要用中括号[]
#numpy.random.randn(d0, d1, …, dn),其中d0, d1, …, dn)为整数型，随机输出标准正态分布的矩阵
X = np.r_[np.random.randn(20,2)-[2,2],np.random.randn(20,2)+[2,2]]
Y = [0]*20 + [1]*20      #将前20个点归为一类，后20个点归为另一类

#创建分类器对象并训练分类器模型
clf = svm.SVC(kernel='linear')
clf.fit(X,Y)

#方程：w0*x+w1*y+w3=0 --> y = (-w0/w1)*x-w3/w1
w = clf.coef_[0]                       #权重向量（二维）  coef_存放回归系数
a = -w[0]/w[1]                         #直线的斜率
x = np.linspace(-5,5)                  #在指定间隔（-5,5）之间产生等差数列作为x坐标的值
y = a * x -(clf.intercept_[0])/w[1]    #intercept_[0]存放截距w3

b = clf.support_vectors_[0]        #第一个支持向量的点
y_down = a * x + (b[1] - a*b[0])   #超平面下方的直线的方程
b = clf.support_vectors_[-1]       #最后一个支持向量点
y_up = a * x + (b[1] - a*b[0])     #超平面上方的直线的方程

print("weight vector:",w)         #输出权重向量w
print("ratio:",a)		  #输出斜率
print("support vectors",clf.support_vectors_)    #输出支持向量点
print("clf.coef_",clf.coef_)        #clf.coef_存放回归系数

#画图
pl.plot(x,y,'k-')         #画出超平面
pl.plot(x,y_down,'k--')   #与支持向量相切下面的直线
pl.plot(x,y_up,'k--')     #与支持向量相切上面的直线

pl.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,1],s=80,facecolors='none')   #绘制出支持向量点
pl.scatter(X[:,0],X[:,1],c=Y,cmap=pl.cm.Paired)      #绘制出随机生成的40个点
pl.axis('tight')        #调整坐标和你输入的数据范围一致
pl.show()

运行结果为：

weight vector: [ 0.90230696  0.64821811]
ratio: -1.39198047626
support vectors [[-1.02126202  0.2408932 ]
 [-0.46722079 -0.53064123]
 [ 0.95144703  0.57998206]]
clf.coef_ [[ 0.90230696  0.64821811]]