from numpy import *
import matplotlib.pyplot as plt
class optStruct:
def __init__(self, dataMatIn, classLabels, C, toler):
self.X = dataMatIn
self.labelMat = classLabels
self.C = C
self.tol = toler
self.m = shape(dataMatIn)[0]
self.alphas = mat(zeros((self.m, 1)))
self.b = 0
self.eCache = mat(zeros((self.m, 2)))
def loadDataSet(fileName):
"""loadDataSet(对文件进行逐行解析,从而得到每行的类标签和整个数据矩阵)
Args:
fileName 文件名
Returns:
dataMat 数据矩阵
labelMat 类标签
"""
dataMat = []
labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]), float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat, labelMat
def selectJrand(i, m):
"""
随机选择一个整数
Args:
i 第一个alpha的下标
m 所有alpha的数目
Returns:
j 返回一个不为i的随机数,在0~m之间的整数值
"""
j = i
while j == i:
j = int(random.uniform(0, m))
return j
def clipAlpha(aj, H, L):
"""clipAlpha(调整aj的值,使aj处于 L<=aj<=H)
Args:
aj 目标值
H 最大值
L 最小值
Returns:
aj 目标值
"""
if aj > H:
aj = H
if L > aj:
aj = L
return aj
def calcEk(oS, k):
"""calcEk(求 Ek误差:预测值-真实值的差)
该过程在完整版的SMO算法中陪出现次数较多,因此将其单独作为一个方法
Args:
oS optStruct对象
k 具体的某一行
Returns:
Ek 预测结果与真实结果比对,计算误差Ek
"""
fXk = float(multiply(oS.alphas, oS.labelMat).T * (oS.X * oS.X[k, :].T)) + oS.b
Ek = fXk - float(oS.labelMat[k])
return Ek
def selectJ(i, oS, Ei):
"""selectJ(返回最优的j和Ej)
内循环的启发式方法。
选择第二个(内循环)alpha的alpha值
这里的目标是选择合适的第二个alpha值以保证每次优化中采用最大步长。
该函数的误差与第一个alpha值Ei和下标i有关。
Args:
i 具体的第i一行
oS optStruct对象
Ei 预测结果与真实结果比对,计算误差Ei
Returns:
j 随机选出的第j一行
Ej 预测结果与真实结果比对
,计算误差Ej
"""
maxK = -1
maxDeltaE = 0
Ej = 0
oS.eCache[i] = [1, Ei]
validEcacheList = nonzero(oS.eCache[:, 0].A)[0]
if (len(validEcacheList)) > 1:
for k in validEcacheList:
if k == i:
continue
Ek = calcEk(oS, k)
deltaE = abs(Ei - Ek)
if (deltaE > maxDeltaE):
maxK = k
maxDeltaE = deltaE
Ej = Ek
return maxK, Ej
else:
j = selectJrand(i, oS.m)
Ej = calcEk(oS, j)
return j, Ej
def updateEk(oS, k):
"""updateEk(计算误差值并存入缓存中。)
在对alpha值进行优化之后会用到这个值。
Args:
oS optStruct对象
k 某一列的行号
"""
Ek = calcEk(oS, k)
oS.eCache[k] = [1, Ek]
def innerL(i, oS):
"""innerL
内循环代码
Args:
i 具体的某一行
oS optStruct对象
Returns:
0 找不到最优的值
1 找到了最优的值,并且oS.Cache到缓存中
"""
Ei = calcEk(oS, i)
'''
# 检验训练样本(xi, yi)是否满足KKT条件
yi*f(i) >= 1 and alpha = 0 (outside the boundary)
yi*f(i) == 1 and 0
if ((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0)):
j, Ej = selectJ(i, oS, Ei)
alphaIold = oS.alphas[i].copy()
alphaJold = oS.alphas[j].copy()
if (oS.labelMat[i] != oS.labelMat[j]):
L = max(0, oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else:
L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
if L == H:
print("L==H")
return 0
eta = 2.0 * oS.X[i, :] * oS.X[j, :].T - oS.X[i, :] * oS.X[i, :].T - oS.X[j, :] * oS.X[j, :].T
if eta >= 0:
print("eta>=0")
return 0
oS.alphas[j] -= oS.labelMat[j] * (Ei - Ej) / eta
oS.alphas[j] = clipAlpha(oS.alphas[j], H, L)
updateEk(oS, j)
if (abs(oS.alphas[j] - alphaJold) < 0.00001):
print("j not moving enough")
return 0
oS.alphas[i] += oS.labelMat[j] * oS.labelMat[i] * (alphaJold - oS.alphas[j])
updateEk(oS, i)
b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :] * oS.X[i, :].T - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.X[i, :] * oS.X[j, :].T
b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :] * oS.X[j, :].T - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.X[j, :] * oS.X[j, :].T
if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]):
oS.b = b1
elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]):
oS.b = b2
else:
oS.b = (b1 + b2) / 2.0
return 1
else:
return 0
def smoP(dataMatIn, classLabels, C, toler, maxIter):
"""
完整SMO算法外循环,与smoSimple有些类似,但这里的循环退出条件更多一些
Args:
dataMatIn 数据集
classLabels 类别标签
C 松弛变量(常量值),允许有些数据点可以处于分隔面的错误一侧。
控制最大化间隔和保证大部分的函数间隔小于1.0这两个目标的权重。
可以通过调节该参数达到不同的结果。
toler 容错率
maxIter 退出前最大的循环次数
Returns:
b 模型的常量值
alphas 拉格朗日乘子
"""
oS = optStruct(mat(dataMatIn), mat(classLabels).transpose(), C, toler)
iter = 0
entireSet = True
alphaPairsChanged = 0
'''
外层循环首先遍历所有满足0到C范围内的alpha,即在间隔边界上的支持向量点,
检验它们是否满足KKT条件。如果这些样本点都满足KKT条件,那么遍历整个训练集,检验它们是否满足KKT条件。
'''
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
alphaPairsChanged = 0
if entireSet:
for i in range(oS.m):
alphaPairsChanged += innerL(i, oS)
print("fullSet, iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
iter += 1
else:
nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
for i in nonBoundIs:
alphaPairsChanged += innerL(i, oS)
print("non-bound, iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
iter += 1
if entireSet:
entireSet = False
elif (alphaPairsChanged == 0):
entireSet = True
print("iteration number: %d" % iter)
return oS.b, oS.alphas
def calcWs(alphas, dataArr, classLabels):
"""
基于alpha计算w值
Args:
alphas 拉格朗日乘子
dataArr feature数据集
classLabels 目标变量数据集
Returns:
wc 回归系数
"""
X = mat(dataArr)
labelMat = mat(classLabels).transpose()
m, n = shape(X)
w = zeros((n, 1))
for i in range(m):
w += multiply(alphas[i] * labelMat[i], X[i, :].T)
return w
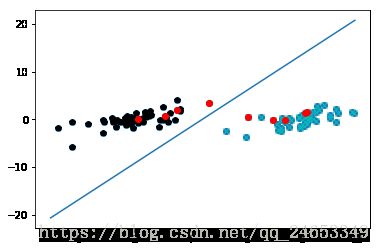
def plotfig_SVM(xArr, yArr, ws, b, alphas):
"""
参考地址:
http://blog.csdn.net/maoersong/article/details/24315633
http://www.cnblogs.com/JustForCS/p/5283489.html
http://blog.csdn.net/kkxgx/article/details/6951959
"""
xMat = mat(xArr)
yMat = mat(yArr)
b = array(b)[0]
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xMat[:, 0].flatten().A[0], xMat[:, 1].flatten().A[0])
x = arange(-1.0, 10.0, 0.1)
y = (-b-ws[0, 0]*x)/ws[1, 0]
ax.plot(x, y)
for i in range(shape(yMat[0, :])[1]):
if yMat[0, i] > 0:
ax.plot(xMat[i, 0], xMat[i, 1], 'cx')
else:
ax.plot(xMat[i, 0], xMat[i, 1], 'kp')
for i in range(100):
if alphas[i] > 0.0:
ax.plot(xMat[i, 0], xMat[i, 1], 'ro')
plt.show()
if __name__ == "__main__":
dataArr, labelArr = loadDataSet('6.SVM/testSet.txt')
b, alphas = smoP(dataArr, labelArr, 0.6, 0.001, 40)
print '\n\n\n'
print 'b=', b
print 'alphas[alphas>0]=', alphas[alphas > 0]
print 'shape(alphas[alphas > 0])=', shape(alphas[alphas > 0])
for i in range(100):
if alphas[i] > 0:
print dataArr[i], labelArr[i]
ws = calcWs(alphas, dataArr, labelArr)
plotfig_SVM(dataArr, labelArr, ws, b, alphas)