机器学习之SVM算法（一）KKT条件

前言

　　本文旨在详细介绍KKT条件的推导和计算方法。
　　拉格朗日算子常用语等式约束最优化的求解中，是KKT条件的特殊形式。KKT条件用于含有不等式约束的条件下的优化问题，例如SVM算法。要深入理解SVM算法必需深入理解KKT条件，本文尝试使用简单易懂的方法向读者介绍KKT条件的推导和使用方法。博主尽量使用图形来阐述KKT条件的深层内涵，数学功底较弱的读者可直接跳过推导过程看结论和例子。

拉格朗日乘子法

　　考虑如下约束条件下的：
　　

minxf(x)s.t.hi(x)=0i=1,2,⋯k

　　其中：
　　

x∈Rn

　　本博客以二元函数为例介绍拉格朗日乘子法的推导过程。
　　考虑如下优化问题： f(x,y) 满足约束 h(x,y)=0
　　如果在 (x0,y0) 处取得极值，那么有:
　　

h(x0,y0)=0

　　约束条件确定一个连续且具有连续导数的函数：
　　

y=φ(x)

　　这时，原问题为：
　　

f(x,φ(x))

　　上式在 (x0,y0) 处取得极值，由一元可导函数取得极值的必要条件知道：
　　

fx(x0,y0)+fy(x0,y0)dydx∣∣∣x=x0=0

　　由隐函数求导公式有：
　　

dydx∣∣∣x=x0=−hx(x0,y0)hy(x0,y0)

　　所以有：
　　

fx(x0,y0)−fy(x0,y0)hx(x0,y0)hy(x0,y0)=0

　　引入 λ ，有：
　　

fx(x0,y0)hx(x0,y0)=fy(x0,y0)hy(x0,y0)=−λ

　　这样，上述必要条件就变为：
　　

fx(x0,y0)+λhx(x0,y0)=0fy(x0,y0)+λhy(x0,y0)=0h(x0,y0)=0

　　若引入辅助函数：
　　

L(x,y)=f(x,y)+λh(x,y)

　　这不难看出，上述极值条件为：
　　

Lx(x,y)=0Ly(x,y)=0Lλ(x,y)=0

　　推广到多元情况为：
　　

L(x1,⋯,xn)=f(x1,⋯,xn)+∑ikαihi(x1,⋯,xn)

　　 L(x1,⋯,xn) 的极值点即原问题的极值点。
　　即满足以下条件的点即原问题的最优解：

∇Lxi(x1,⋯,xn)=0 i=1,⋯,n∇Lαj(x1,⋯,xn)=0j=1,⋯,k

　　以下以几何形式阐述这一原理：

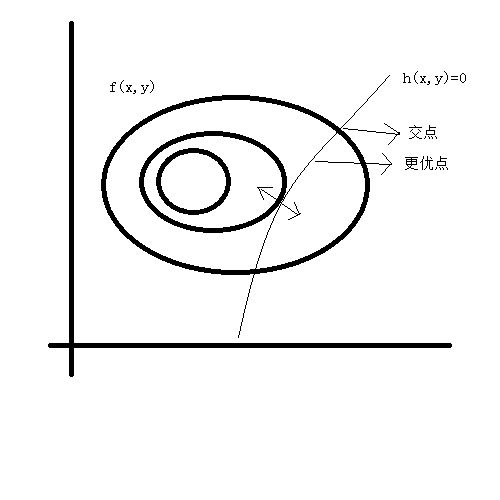
　　图中的用等高线表示 f(x,y) 。由于原优化问题是凸优化问题，当 h(x,y)=0 和等高线相交时意味着在两个交点之间存在更优的点。只有当等高线和 h(x,y)=0 相切时才是满足约束条件的最优点。即在交点处满足：
　　

∇f(x,y)=−λ∇h(x,y)h(x,y)=0

　　以下以一例子说明拉格朗日乘子法的计算步骤。

未完待续。。。
/**********************
* 本文来自博客 “zhb_bupt“
* 转载请标明出处:http://blog.csdn.net/zhb_bupt
* 博客迁往： http://deepminer.ailifenet.com
********************************/