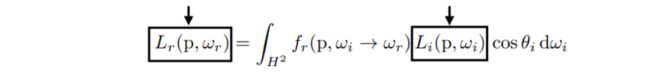GAMES101-现代计算机图形学入门-闫令琪 - lecture15 光线追踪3 - 辐射度量学、渲染方程(Ray Tracing 3) - 课后笔记
光线追踪3 - 辐射度量学、渲染方程和全局光照
内容:
- 辐射度量学
- 光线传输(Light transport)
- 反射方程(The reflection equation)
- 渲染方程(The rendering equation)
- 全局光照(Global illumination)
辐射度量学
Radiant energy:辐射能量,单位位焦耳J,在图形学中几乎不用
Radiant flux(power):单位时间内辐射出的能量
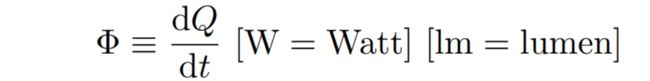
Radiant Intensity:在单位时间内,往每个立体角(Solid Angle)上辐射出的能量
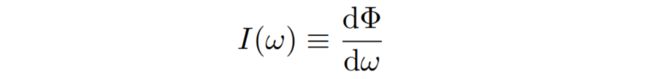
立体角(Solid Angle):球体上对应面积与半径的平方的比值
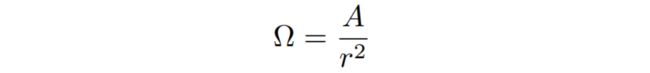
单位立体角(Differential Solid Angles):单位面积对应的立体角的大小,dA表示单位面积,dw表示单位立体角
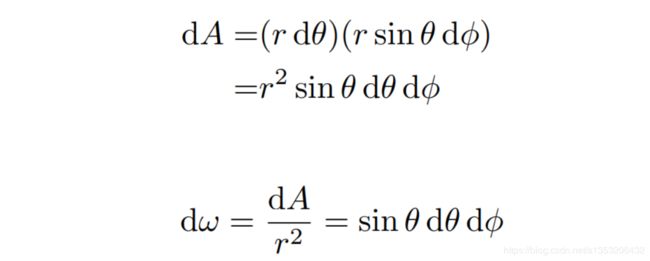
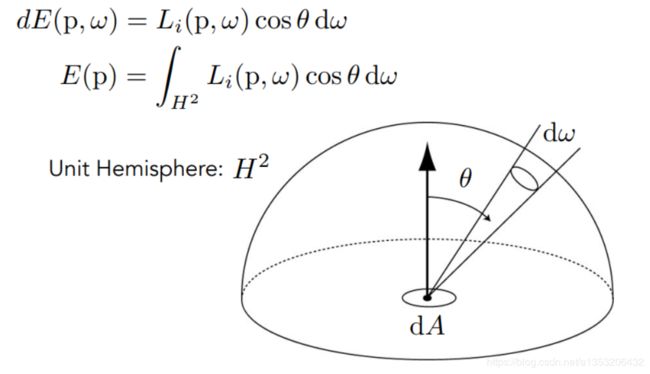
Irradiance
定义:在单位时间内,每个单位面积上接受到的光照的能量,Radiant Intensity的微分/面积的微分。注:这个单位面积必须要和光线垂直,如果不垂直的话要把面积投影到垂直的方向上,类似之前的Biling - Phong里的内容。
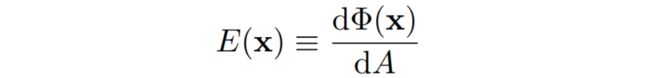
Lambert’s Cosine Law
- 左图:单位面积和光线垂直,所以直接用Irradiance的计算式即可
- 中图:面积与光线不垂直,其投影只能接受到三根、一半的光线,所以要×1/2
- 右图:更普遍的情况,当单位面积与光线不垂直时,要×cos将其投影到垂直的方向上去。
为什么地球会出现四季的变换?
上面的Lambert’s余弦定理就解释了地球为什么会出现四季变换。

当北半球是夏天时,太阳光直射北半球,北半球接收到的光的能量更多,也就更热;而当北半球是冬天时,光线与地球的表面有一定的夹角,吸收的能量减少,所以冬天就更冷。(如上图地球中黑色虚线处)
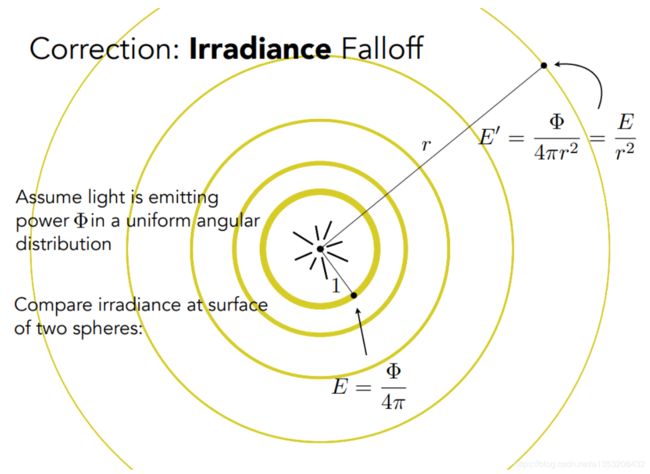
用Irradiance解释能量的衰减
之前曾经说过,我们是假设能量集中在一个球壳上,随着球壳的增大,光的强度会有一个r平方的衰减;
现在可以用Irradiance正确解释:在最内部的单位球上,Irradiance(E) = φ/4π,单位面积上接受到的能量就是φ/4π,而在外部的球面上,Irradiance(E’) = φ/4πr^2,,在单位面积上接受到的能量就是 φ/4πr^2,所以就是r平方的衰减。
所以就可以知道,在这里衰减的并不是Radiant Intensity,而是Irradiance在衰减。如果从球心以一个立体角画一个锥形,就可以知道,随着球面越来越大,立体角的大小是不变的,而立体角对应单位面积的大小却越来越大,所以球面越大时,dA越大,Irradiance也就会越小。
Radiance
Radiance时描述环境中光的分布的基本场量(fundamental field quantity)
- 主要用来准确描述光线的一些属性
- 准确的光线追踪与radiance关系非常大,渲染就是在计算radiance
定义:
英文定义:The radiance (luminance) is the power emitted, reflected, transmitted or received by a surface, per unit solid angle, per projected unit area.
定义:radiant power(flux)在每个单位立体角、每个投影的面上有多少
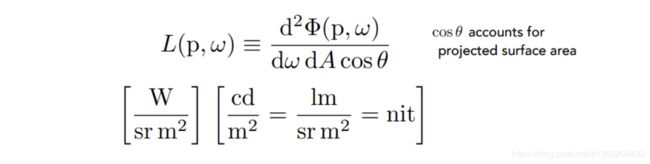
定义中有两个”每“,所以这里要做两次微分,其中做θ是面的投影时用到的角度

Radiance如上图所示:dA为一个单位面积,该单位面积有自己的方向,所以和入射的光线会有一个夹角θ,然后从这个面往某个方向w上辐射出一些能量。
联系
Radiance :Radiant power(flux) per unit solid angle , per projected unit area.
Irradiance : Radiant power per projected unit area.
Radiant Intensity : power per solid angle
所以上面三个物理量联系起来就是:
Radiance : Irradiance per solid angle
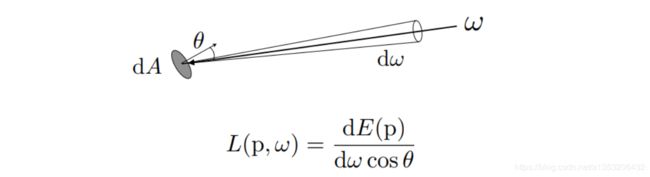
按照这种联系解释就是说:Radiance表示单位面积dA将接受到的能量朝w方向辐射出的能量。同样,反过来也可以说从w方向发射来的Radiance到dA上一共接受得到了Irradiance的能量。
Radiance: Radiant Intensity per projected unit area
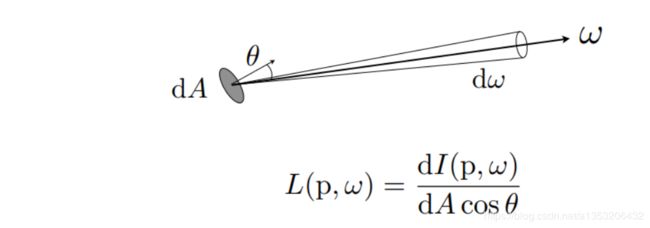
Intensity代表的是向单位立体角的方向上辐射出的能量,这里Radiance就代表在某个单位面积的投影上的Intensity
Radiance和Irradiance的区别
双向反射分布函数(Bidirectional Reflectance Distribution Function,BRDF)
反射
在之前说过,反射就是一道光线到达一个表面,然后反射到其他的方向去;这个过程其实也可以看作是从某一个方向来的光线到达物体表面后被物体表面所吸收,然后再由物体表面发射到其他方向去,如下图所示:

dE(wi)表示从wi方向射来的radiance到达反射点时被吸收转化得到的Irradiance(其实就是反射点从某一个方向接收到的能量转化为自己的能量之后然后再辐射出去),下面的等式可以通过前面的内容变换得到。
![]()
dL(x,wr)则表示反射点向wr方向反射出去的radiance。
我们知道反射点要吸收来自某一个方向的radiance然后反射到四面八方的立体角上,但是我们不知道反射到wr的方向上会有多少能量。
所以我们就定义一个函数,计算出:考虑一个微小的面积dA,从某一个微小的立体角dwi上接受到的Irradiance,会如何被分配到各个立体角上。其实求得就是一个比例,是什么比例?这个比例是 对于任何一个立体角上发出去的Radiance / 单位面积接收到的Irradiance,这就是BRDF的定义。它会告诉我们如何把表面上收集到的能量以某一种比例放射到其他的方向上去。
BRDF
BRDF能表示从每个入射方向收集到的能量以某种比例反射到每个出射方向上的能量。
就是说某个光线打到物体表面后,往不同方向反射的能量分布。如果说是镜面反射,那么只有反射方向上会有能量,其他所有方向上都没有能量;如果是漫反射,就会告诉我,这个进来的能量会被均等的分布到各个方向上。
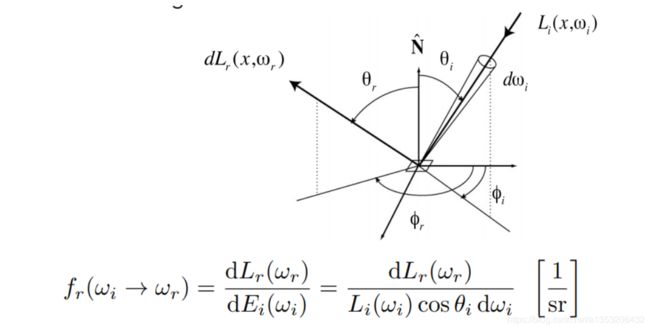
忽略其推导部分,其实BRDF就是描述了物体和光线之间的相互作用。正是由于BRDF的这种概念,决定了物体不同的材质到底是怎么一回事,也就是BRDF定义了材质。
反射方程(The Reflection Equation)
由上面的式子我们可以得到:
![]()
从wi角度入射的能量最后反射到wr方向上的能量为dLr(wr)。
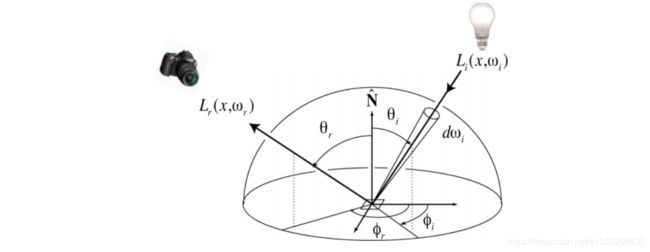
而在反射的过程,我们并不是只对单一的,来自某一个方向的能量进行反射,而是要将来自四面八方的能量都收集起来,然后反射到某一个角度上,所以要得到最终的反射效果,应该是:
- 通过BRDF计算出每个接受的能量反射到wr方向上的能量
- 然后把这些能量全部累加起来,得到就是wr方向上反射的能量。
用积分表示就是:
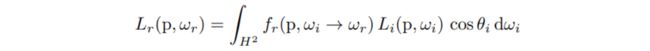
其中H的平方表示的积分面积为整个半球面。上面的整个表达式就是反射方程。
挑战:递归等式、
- 反射点接受的能量(Irradiance)并不只是来自于光源,还会来自别的表面反射来的光(Irradiance)
- 从反射点反射出去的能量(Radiance)也并不只会反射到Camera或者人眼,还会作为Irradiance反射到其他的面上。
所以反射方程的定义就成了一个递归的定义,也因此,光线反射的次数不同,得到的最终效果也就不会不同。
但是我们目前先不考虑这些,我们先学一个通用的方程即可。
渲染方程(The Rendering Euqation)
渲染方程很简单,与反射方程相比,渲染方程只是多加了一个自己发光的能量。因为我们在考虑物体表面对光进行反射的时候,没有考虑物体自己发光的情况,所以渲染方程就加上了物体自身发光的能量。反射光 + 自身 发光 = 渲染效果,渲染方程如下:

其中Le是物体自身发的光,后面的积分是反射光。