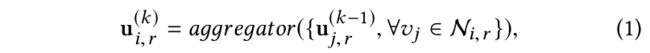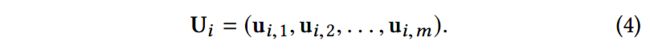【论文解读 KDD 2019 | GATNE 】Representation Learning for Attributed Multiplex Heterogeneous Network
论文链接:https://arxiv.org/abs/1905.01669
代码链接:https://github.com/cenyk1230/GATNE
来源:KDD 2019
作者本人写的论文讲解:阿里电商场景下的大规模异构网络表示学习
文章目录
- 1 摘要
- 2 介绍
- 2.1 挑战
- 2.2 作者提出
- 3 问题定义
- 4 方法
- 4.1 Transductive Model: GATNE-T
- 4.2 Inductive Model: GATNE-I
- 4.3 模型优化
- 5 实验
- 6 总结
1 摘要
本文解决的是Attributed Multiplex Heterogeneous Networks(属性多重异质网)的嵌入学习问题。
本文提出的模型支持直推学习(transductive)和推理学习(inductive)。
在Amazon、Youtube、Twitter和Alibaba四个数据集上进行了链接预测实验,本文提出的模型超越了state-of-the-art的效果。模型还成功应用在了阿里巴巴电商平台的推荐系统中,证明了有效性和高效性。
2 介绍
本文解决的是属性多重异质网(AMHENs)的嵌入学习问题,图中有多种类型的节点和多种类型的边,并且每个节点都有不同的属性。
多重异质网(MHEN)嵌入学习:节点之间存在多种邻近(proximities)类型,产生具有多个视图(views)的网络,就需要进行多重网络嵌入学习。
2.1 挑战
处理AMHENs面临的挑战如下:
(1)Multiplex Edges(复用边)
每个节点对可能具有多种不同类型的关系。应从不同的关系中学习到特征,进而学习到统一的嵌入表示。
(2)Partial Observations
真实的网络数据通常是部分被观测的,也就是inductive learning问题。例如,一个long-tailed顾客可能与一些商品的交互很少。现有的大多数方法都聚焦于transductive settings,不能处理long-tailed和冷启动问题。
(3)可扩展性
算法要具有可扩展性,能在大型图上应用落地。
2.2 作者提出
提出GATNE(General Attributed Multiplex HeTerogeneous Network Embedding)模型,获取了丰富的属性信息并且利用了不同节点的多重拓扑结构。
GATNE的主要特点如下:
(1)定义了属性复用异质图嵌入问题;
(2)GATNE支持直推式学习和归纳式学习。并且理论证明了本文的直推式模型比现有的模型更一般化。
(3)有很好的可扩展性,可处理上亿级别的节点和十亿级别的边。
3 问题定义
一些符号定义如下:
异质图: G = ( V , E ) G=(V,E) G=(V,E),节点类型数+边类型数$\geq$2
属性图: G = ( V , E , A ) G=(V,E,A) G=(V,E,A), A = { x i ∣ v i ∈ V } A={\{x_i|v_i\in V\}} A={xi∣vi∈V}是节点特征集合。
属性多重异质网(AMHEN): G = ( V , E , A ) , E = ⋃ r ∈ R E r G=(V,E,A), E=\bigcup_{r\in R}E_r G=(V,E,A),E=⋃r∈REr, E r E_r Er表示所有类型为r的边。作者将网络按照边的类型分解成 G r = ( V , E r , A ) G_r=(V,E_r,A) Gr=(V,Er,A)。
AMHEN嵌入学习:给定AMHEN G = ( V , E , A ) G=(V,E,A) G=(V,E,A),为每个节点学习到统一的低维空间表示。
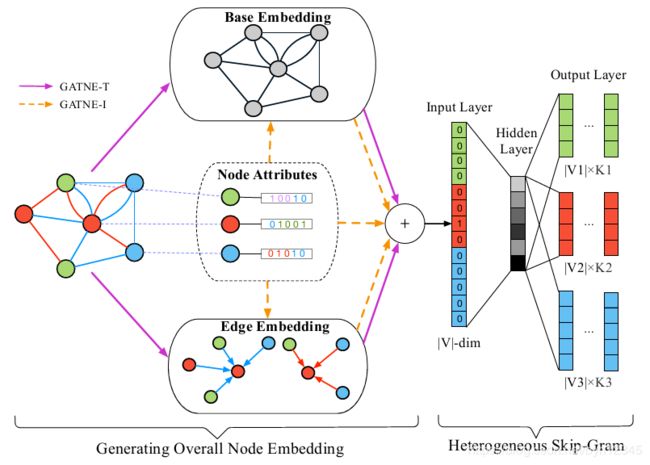
下图就是AMHEN的一个例子:
图的左边用户和商品都分别有多个属性,而且用户和商品之间的连边类型也是多样的,一个用户和一个商品可能有多个类型不同的连边。图的中间部分是将左边的图分别形式化为了:AMHEN(属性多重异质网)、MHEN(多重异质网)和HON(同质网)。右边是,三种方法的实验效果对比。
4 方法
分别介绍直推式的模型(GATNE-T)和归纳式的模型(GATNE-I)。
由于有多种类型的边(比如点击、购买),这里我们考虑给每个节点在每种边类型下都学一个表示。比如我们给用户和商品在点击场景下学一种表示,在购买场景下学一种表示。但是这两种表示之间并不是完全独立的,是通过某种机制互相影响的。我们主要考虑的就是如何来建模不同类型的表示之间相互影响的方式。
4.1 Transductive Model: GATNE-T
在GATNE-T模型中,将节点 v i v_i vi在边类型 r r r上的embedding分成两部分:基类嵌入(base embedding)和边嵌入(edge embedding),如上图所示。
节点 v i v_i vi的基类嵌入在不同类型边中共享。
节点 v i v_i vi在边类型 r r r上的第k层的边嵌入 u i , r ( k ) ∈ R s , ( 1 ≤ k ≤ K ) u^{(k)}_{i,r}\in R^s, (1\leq k\leq K) ui,r(k)∈Rs,(1≤k≤K),是通过聚合邻居边信息得到的,计算如下:
其中 N i , r N_{i,r} Ni,r是由 r r r类型的边连接的节点 v i v_i vi的邻居节点。 u i , r ( 0 ) u^{(0)}_{i,r} ui,r(0)是随机初始化的。
上式的聚合函数可以使用GraphSAGE中的mean聚合:
也可以使用池化聚合方法,例如max-pooling聚合:
然后将节点 v i v_i vi的所有边嵌入拼接,其中 U i ∈ R ( s × m ) U_i\in R^{(s\times m)} Ui∈R(s×m):
使用自注意力机制计算注意力系数 a i , r ∈ R m a_{i,r}\in R^m ai,r∈Rm:
其中 w r ∈ R d a , W r ∈ R d a × s w_r\in R^{d_a}, W_r\in R^{d_a\times s} wr∈Rda,Wr∈Rda×s是对于 r r r类型边,需要训练的参数。
所以,节点 v i v_i vi对于r类型边的整体embedding表示如下:
其中 b i b_i bi是节点 v i v_i vi的基类向量, α r \alpha_r αr是表示边嵌入权重的超参数, M r ∈ R s × d M_r\in R^{s\times d} Mr∈Rs×d是需要训练的转换矩阵。
然后作者对比了本文的GATNE-T和最新提出的MNE(Hongming Zhang, Liwei Qiu, Lingling Yi, and Yangqiu Song. 2018. Scalable Multiplex Network Embedding. In IJCAI’18. )。区别在于GATNE-T为不同类型的边分配了注意力。
直推式模型GATNE-T只是聚合了节点的邻居信息,没有应用到节点的属性信息,并且聚合的时候按照边的类型进行了分类,生成节点 v i v_i vi对于 r r r类型边的嵌入表示。而且在计算点 v i v_i vi对于 r r r类型边的嵌入表示时,还使用注意力机制,为不同类型的边分配了不同的注意力。
由上面的公式可知, u i , r u_{i,r} ui,r都是通过聚合邻居得到的,训练的参数都是一个整体的矩阵。所以,GATNE-T不能单独为新加入的节点生成嵌入表示,也就是不能使用训练集训练好的参数用于生成(训练时不可见的)测试集的节点嵌入表示,必须重新训练。也就是说GATNE-T只能进行直推式学习(transductive learning),不能进行归纳式学习(inductive learning)。
4.2 Inductive Model: GATNE-I
GATNE-T不能处理不可见的节点,也就是说它只能为训练中出现过的节点生成embedding,即直推式学习(transductive learning),不能进行归纳式学习(inductive learning)。
为了可以进行归纳式学习,接着提出了GATNE-I模型,也是如4.1中的图所示。
首先,定义基类向量 b i b_i bi为节点 v i v_i vi的属性 x i x_i xi的函数: b i = h z ( x i ) b_i=h_z(x_i) bi=hz(xi)。其中 h z h_z hz是转换函数, z = ϕ ( i ) z=\phi (i) z=ϕ(i)是节点 v i v_i vi的边类型。
不同类型的节点,属性的维度可能也不同。这就要求转换函数 h z h_z hz有不同的形式,例如多层感知机。
类似地,边嵌入的初始值 u i , r ( 0 ) u^{(0)}_{i,r} ui,r(0)也应是属性 x i x_i xi的函数: u i , r ( 0 ) = g z , r ( x i ) u^{(0)}_{i,r}=g_{z,r}(x_i) ui,r(0)=gz,r(xi)。其中 g z , r g_{z,r} gz,r也是一个转换函数,将属性特征转换为节点 v i v_i vi关于 r r r类型边的边嵌入。其中 z z z是节点 v i v_i vi的类型。
对于节点 v i v_i vi关于 r r r类型边的嵌入,归纳式模型还多增加了一个属性项:
其中, β r \beta_r βr是系数, D z D_z Dz是类型为 z z z的节点 v i v_i vi对应的特征转换矩阵。
直推式模型和归纳式模型的区别在于:基类向量** b i b_i bi和初始边嵌入 u i , r ( 0 ) u^{(0)}_{i,r} ui,r(0)**的生成方式。
- 在直推式模型中, b i b_i bi和 u i , r ( 0 ) u^{(0)}_{i,r} ui,r(0)是基于网络结构,为每个节点直接训练的。所以,无法处理训练中未出现过的节点。
- 在归纳式模型中,训练的是转换函数 h z h_z hz和 g z , r g_{z,r} gz,r,将原始特征 x i x_i xi转换为 b i b_i bi和 u i , r ( 0 ) u^{(0)}_{i,r} ui,r(0)。并非为每个节点直接训练 b i b_i bi和 u i , r ( 0 ) u^{(0)}_{i,r} ui,r(0)。这就可以处理训练中未出现的节点,只要这个节点有特征 x x x。
归纳式模型之所以可以处理训练中未出现过的节点,是因为它并不是为每个节点直接训练 b i b_i bi和 u i , r ( 0 ) u^{(0)}_{i,r} ui,r(0),而是训练节点特征 x i x_i xi的转换函数: h z h_z hz和 g z , r g_{z,r} gz,r。也就是说,为新加入的节点生成嵌入表示时,用到了节点的属性特征信息 x i x_i xi,为了生成边嵌入,聚合的也是邻居节点的属性特征信息。
4.3 模型优化
使用基于元路径(meta-path-based)的随机游走生成节点序列,然后输入skip-gram模型,生成嵌入表示。
给定原始图分割出来的 r r r视角的图 G r = ( V , E r , A ) G_r=(V,E_r,A) Gr=(V,Er,A),以及元路径模式 T T T,第 t t t步的转移概率为:
给定节点 v i v_i vi和其路径中的上下文 C C C,目标函数是最小化如下的负对数似然,其中 θ \theta θ表示所有参数:
仿照metapath2vec的做法,使用异质的softmax函数。给定 v i v_i vi的条件下 v j v_j vj的概率定义如下:
其中 c k c_k ck是节点 v k v_k vk的context embedding,分子分母中的 v i v_i vi是节点 v i v_i vi关于 r r r类型边的整体embedding。
最后,使用负采样技术,对于节点对 ( v i , v j ) (v_i,v_j) (vi,vj),目标函数 − l o g P θ ( v j ∣ v i ) -logP_{\theta}(v_j|v_i) −logPθ(vj∣vi)近似如下:
其中, L L L是针对每个正样本进行负采样得到的负样本数。
算法流程总结如下:
5 实验
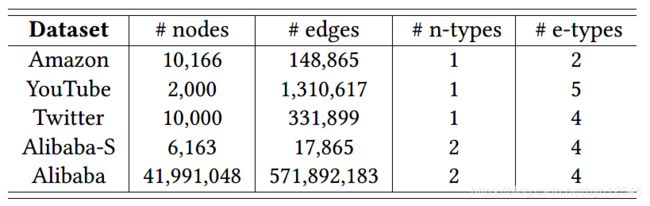
数据集:Amozon, YouTube, Twitter, Alibaba-S(采样), Alibaba
实验任务:链接预测任务
对比方法:
(1)Network Embedding Methods:
DeepWalk, LINE, node2vec。由于这些方法是应用在同质图上的,所以按照不同的边类型先将图分解,再将其输入模型,得到针对每个图的节点嵌入。
(2)Heterogeneous Network Embedding Methods:
metapath2vec
(3)Multiplex Heterogeneous Network Embedding Methods:
PMNE, MVE, MNE
(4)Attributed Network Embedding Methods
ANRL :使用邻居增强的自编码器对节点属性信息建模;使用基于属性解码器的属性感知的skip-gram模型,捕获网络结构特征。
(5)本文的方法:
GATNE-T, GATNE-I。没有节点属性的数据集,为其生成节点特征。
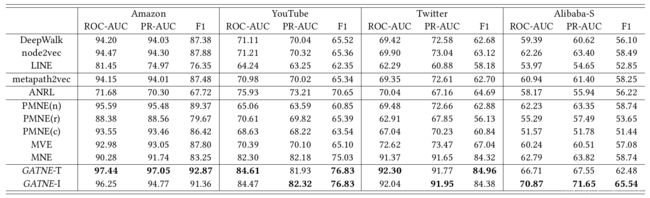
实验结果:
6 总结
本文聚焦于属性多重异质网的嵌入学习问题,提出了GATNE-T和GATNE-I模型分别处理直推式学习和归纳式学习。
将GATNE-I的节点embedding分成三部分:基类向量、边向量、属性向量。
其中基类向量和属性向量在不同类型的边之间是共享的。边向量是聚合邻居信息,并使用注意力机制计算得到的。
链接预测任务超过state-of-the-art,并且在阿里推荐系统中落地应用。
感觉模型挺简单的,只不过应用场景是属性多重异质网,也就是一个user和一个item之间可能有多条不同类型的边。
具体到电商领域,这多种类型的边可以具体为:click(点击)、add-to-preference(添加收藏)、add-to-cart(添加到购物车)、conversion(购买)。
这篇文章模型简单,特点还是偏应用,毕竟已经在阿里的推荐系统中落地了。