机器学习方法篇(13)------KKT条件
● 每周一言
实现目标的最大敌人,是时间。
导语
上一节讲了带等式约束条件的拉格朗日乘子法,本节讲讲带不等式约束条件的函数凸优化方法——KKT条件,为之后深入讲解SVM做准备。
KKT条件
任何不等式约束条件的函数凸优化问题,都可以转化为约束方程小于0且语义不变的形式,以便于使用KKT条件。和上节一样,我们通过一个简单的例子来讲解KKT条件的使用方法。
有如下不等式约束的凸优化问题,求解f的最小值:

转化为约束方程小于(或小于等于)0且语义不变的条件如下:
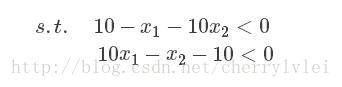
上节说到KKT条件是拉格朗日乘子法的加强版,这个加强版的拉格朗日公式如下:
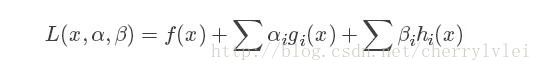
其中,g是不等式约束方程,h是等式约束方程。对于上式函数的凸优化问题,KKT条件一共包含三个条件:
1. L对x的一阶导数为0;
2. h(x) = 0;
3. α·g(x) = 0,α ≥0。
对于第1个条件,就是我们上一节所讲的拉格朗日乘子法;第2个条件,可以作为等式约束条件的语义来理解;而对于第3个条件,言下之意是要么α为0,要么函数g为0。根据加强版的拉格朗日公式,可以写出如下式子:
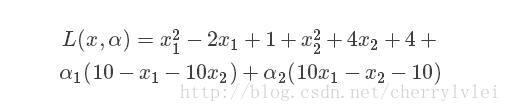
根据KKT条件的第1条,f对x1、x2求偏导,得到:

根据KKT条件的第3条,则可以得到:

接下来就只需要枚举讨论这第3个条件中α和g为0的情况了。这种组合情况一共有4种:α1与α2等于0,α1与g2等于0,α2与g1等于0,g1与g2等于0。
分别计算以上四种情况发现,只有g1与g2等于0满足原方程的解。需要特别注意的是,由于原不等式约束条件是小于,而开口条件存在无限接近的情况,才使得这里的g1和g2可以取0。
以上便是KKT条件的讲解。关于条件的深入证明,有兴趣的读者可以自行查阅资料。敬请期待下节内容。
文中举例来源:http://blog.csdn.net/on2way/article/details/47729419
结语
感谢各位的耐心阅读,后续文章于每周日奉上,敬请期待。欢迎大家关注小斗公众号 对半独白!
