堆 优先队列
首先看完全二叉树的定义:
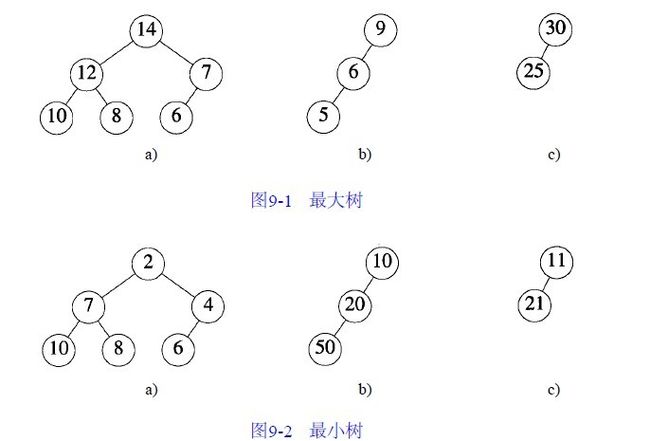
如果一个完全二叉树的某个结点值都不大于或小于他的父结点,那就叫做堆。根结点是所有结点里最大的叫大根堆,最小的叫小根堆。
9-1 a是大根堆,9-2 a是小根堆,剩下的都不是堆(因为不是完全二叉树)。
那么怎么样才能构造出堆呢?
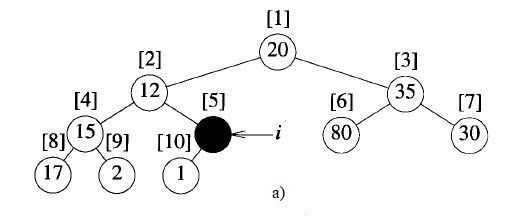
从后往前找到第一个有孩子的结点(肯定在倒数第二排,最后一排已经是堆),看以这个结点为根结点的树满不满足堆的条件,如果不满足就和下面的交换,直到满足堆的条件。就这么一个一个结点检查,一直到根结点,堆就完成了~
比如到结点4(大根堆),15比17小,17没孩子,所以只要把15和17换就行了,此时结点4是17,结点8是15,再到结点2的时候,因为12比17小,所以把17移动到结点2,12又比15小,所以把15移动到结点4,最后把12移动到结点8。
为什么要从后往前呢?这是因为在检查一个结点的时候,如果以他孩子为根结点的树已经是堆,就只要找到这个点应该插入的位置,把子结点都往上移一个就行了~
小根堆代码:
void heapadjust(int i,int l) //检查结点函数,i是这个结点的位置,l是堆的结点数,设根结点为0
{
int child,t;
for(t=a[i]; i*2+1
child=i*2+1; // i是父结点
if(child+1
else break;
}
a[i]=t; //此时已经找到该放的位置,插入t
}
void heapsort(int l)
{
int i,temp;
for(i=l/2-1; i>=0; i--) heapadjust(i,l); //从第1个有孩子的结点开始找,一直到根结点
}
大根堆只要把符号改一下就行了,方法是一样的~
void maxheap_add(int x){
Lmax++;
int child=Lmax,fa=child>>1;
while(fa>0&&a[fa]>=1;
}
a[child]=x;
}
void minheap_add(int x){
Lmin++;
int child=Lmin,fa=child>>1;
while(fa>0&&b[fa]>x){
b[child]=b[fa];
child=fa;
fa>>=1;
}
b[child]=x;
}
void maxheap_adjust(int x){
int t=a[x],fa=x,child=fa<<1;
while(child<=Lmax){
if(child+1<=Lmax&&a[child+1]>a[child]) child++;
if(tb[child]){
b[fa]=b[child];
fa=child;
child=fa<<1;
}
else break;
}
b[fa]=t;
}
int maxheap_del(){
int t=a[1];
a[1]=a[Lmax];
Lmax--;
maxheap_adjust(1);
return t;
}
int minheap_del(){
int t=b[1];
b[1]=b[Lmin];
Lmin--;
minheap_adjust(1);
return t;
} 堆只能保证根结点最大或最小,其他元素并不一定是有序的,但只要每次把根结点和最后一个结点交换,再把剩下无序的结点调整成堆,再把根结点放到后面,再。。重复。。直到最后一个结点,就排完序了~
void heapsort(int l)
{
int i,temp;
for(i=l/2-1; i>=0; i--) heapadjust(i,l);
for(i=l-1;i>0;i--){
temp=a[0]; //交换最后一个和根结点
a[0]=a[i];
a[i]=temp;
heapadjust(0,i);} // 这时除根结点,其他本来已经都是堆,只需检查根结点
}
下面来说优先队列(也是刚发现这个东东。。原理就是堆吧),具体的我也说不好,就简单说下怎么用吧
首先头文件里要有#include
最小值优先:priority_queue
最大值优先:priority_queue
第一个int就是int类型的,vector
顺便说一下STL队列(不是优先队列)
queue
Push():入队,即插入元素
Pop():出队,即删除元素
Front():读取队首元素
Back():读取队尾元素
Empty():判断队列是否为空
Size():队列当前元素
杭电4006
The kth great number
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65768/65768 K (Java/Others)Total Submission(s): 4790 Accepted Submission(s): 1962
刚开始做的是插入元素后就堆排序,输出时就输出a[k],怎么都超时。。后来发现。。只要只在数组里保存k个,在开始构造成一个最小堆,再插入时只要比较要插入的元素和堆的根结点哪个大,如果它比根结点大,就用它代替根结点,这时因为底下的都已经是堆,所以只要调用那个检查结点函数检查根结点就行~(并不需要每次都排序,只要保证堆中k个元素都是目前最大的k个,输出时直接输出根结点就行了(k个最大的里面的最小的))。这道题用优先队列更简单~
最小堆:
#include
int a[1000010];
void heapadjust(int i,int l)
{
int child,t;
for(t=a[i]; i*2+1a[child]) a[i]=a[child];
else break;
}
a[i]=t;
}
void heapsort(int l)
{
int i,temp;
for(i=l/2-1; i>=0; i--) heapadjust(i,l);
}
int main()
{
freopen("D:\\CodeBlocks\\file\\in.txt","r",stdin);
int n,k,t;
char s[5];
while(scanf("%d%d",&n,&k)!=EOF)
{
int l=k,i;
for(i=0; ia[0])
{
a[0]=t;
heapadjust(0,k);
}
}
else
{
printf("%d\n",a[0]);
}
}
}
return 0;
} 优先队列:
#include
#include
#include
#include
using namespace std;
int main()
{
freopen("D:\\CodeBlocks\\file\\in.txt","r",stdin);
int n,k,t;
char s[5];
while(scanf("%d%d",&n,&k)!=EOF)
{
priority_queue,greater >q;
int i,t;
for(i=0; i