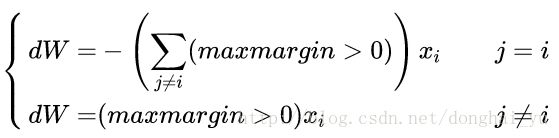cs231n assignment1 --SVM
作业地址:https://github.com/donghaiyu233/cs231n ,欢迎fork~。
先来看一看作业要求:
重点在于SVM的loss function、gradient descent、完成SGD的optimize和W的可视化。话不多说,开始干活!
1.SVM(Support Vector Machine)原理
最终还是因为太懒orz,不如引用经典,以下是自己推荐一看的解释。
最直观的理解:支持向量机(SVM)是什么意思 --知乎
应用上的简单推导:CS231n Linear Classification
还有更严谨的数学推导,可以翻阅李航老师的《统计学习方法》。
最终我们得到full Multiclass SVM loss的式子,其中Δ:安全的距离; λ:regularization strength。(每次看到这里我总会不要自主想到小公主(逃orz)
2.课程作业
linear_svm.py
svm_loss_naive()在课程网站的note上有;需要注意的两点:
1.loss的计算,根据上面给出的公式计算即可
一个实现max(x,0)的小技巧:
margin = (margin > 0) * margin2.导数的计算
根据loss function的公式以及svm_loss_naive的计算过程,我们可以总结出:每个正确的分类即margin<0对dW无贡献,每个错误的分类会产生两个贡献,一个是对正确分类产生-xi贡献,对其对应的错误分类产生xi贡献(对W求偏导的结果)。因此以共对正确分类产生sum(margin>0)次贡献,对每一个错误分类产生一次贡献
可以由以下代码实现,最后加上正则化的导数即为最后的dW
margins01 = 1 * (margins > 0)
margins01[rows,y] = -1*np.sum(margins01, axis=1)
dW = np.dot(X.transpose(), margins01)
dW /= num_trainimport numpy as np
from random import shuffle
#from past.builtins import xrange
def svm_loss_naive(W, X, y, reg):
"""
Structured SVM loss function, naive implementation (with loops).
Inputs have dimension D, there are C classes, and we operate on minibatches
of N examples.
Inputs:
- W: A numpy array of shape (D, C) containing weights.
- X: A numpy array of shape (N, D) containing a minibatch of data.
- y: A numpy array of shape (N,) containing training labels; y[i] = c means
that X[i] has label c, where 0 <= c < C.
- reg: (float) regularization strength
Returns a tuple of:
- loss as single float
- gradient with respect to weights W; an array of same shape as W
"""
dW = np.zeros(W.shape) # initialize the gradient as zero
# compute the loss and the gradient
num_classes = W.shape[1]
num_train = X.shape[0]
loss = 0.0
for i in range(num_train):
scores = X[i].dot(W)
correct_class_score = scores[y[i]]
for j in range(num_classes):
margin = scores[j] - correct_class_score + 1# note delta = 1
#margin = X[i]*W[j] - X[i]*W[y[i]] - 1,后续分别对W[j]与W[y[i]]求偏导
#该类的分数至少要比其它类的分数高1
if margin > 0:
if j != y[i]:
#如果是同一类,则跳过,因为此时margin为delta.
loss += margin
dW[:, y[i]] += -1 * X[i]
dW[:, j] += 1 * X[i]
# Right now the loss is a sum over all training examples, but we want it
# to be an average instead so we divide by num_train.
loss /= num_train
dW /= num_train
# Add regularization to the loss.
#W * W == np.square(W,W),对矩阵中的元素进行操作
loss += reg * np.sum(W * W)
dW += 2*reg*W
#broadcast,加上正则项后的dW
#############################################################################
# TODO: #
# Compute the gradient of the loss function and store it dW. #
# Rather that first computing the loss and then computing the derivative, #
# it may be simpler to compute the derivative at the same time that the #
# loss is being computed. As a result you may need to modify some of the #
# code above to compute the gradient. #
#############################################################################
return loss, dW
def svm_loss_vectorized(W, X, y, reg):
"""
Structured SVM loss function, vectorized implementation.
Inputs and outputs are the same as svm_loss_naive.
"""
loss = 0.0
dW = np.zeros(W.shape) # initialize the gradient as zero
#############################################################################
# TODO: #
# Implement a vectorized version of the structured SVM loss, storing the #
# result in loss. #
#############################################################################
scores = np.dot(X,W)
#scores:[num_train,C]
num_train = X.shape[0]
rows = range(num_train)
correct_class_score = scores[rows,y]
#correct_class_score:[1,num_train]
margins = np.maximum(0,scores-np.reshape(correct_class_score,[num_train,1])+1)
margins[rows,y] = 0
loss = np.sum(margins)
loss /= num_train
loss += 0.5 * reg * np.sum(W * W)
#############################################################################
# END OF YOUR CODE #
#############################################################################
#############################################################################
# TODO: #
# Implement a vectorized version of the gradient for the structured SVM #
# loss, storing the result in dW. #
# #
# Hint: Instead of computing the gradient from scratch, it may be easier #
# to reuse some of the intermediate values that you used to compute the #
# loss. #
#############################################################################
margins01 = 1 * (margins > 0)
margins01[rows,y] = -1*np.sum(margins01, axis=1)
dW = np.dot(X.transpose(), margins01)
dW /= num_train
dW += reg * W
#############################################################################
# END OF YOUR CODE #
#############################################################################
return loss, dWlinear_classifier.py
利用np.random.choice()进行又放回的抽样(速度更快),返回的choice作为抽样的索引;其余与梯度下降一样。
from __future__ import print_function
import numpy as np
from cs231n.classifiers.linear_svm import *
from cs231n.classifiers.softmax import *
from past.builtins import xrange
class LinearClassifier(object):
def __init__(self):
self.W = None
def train(self, X, y, learning_rate=1e-3, reg=1e-5, num_iters=100,
batch_size=200, verbose=False):
"""
Train this linear classifier using stochastic gradient descent.
使用SGD训练线性分类器
Inputs:
- X: A numpy array of shape (N, D) containing training data; there are N
training samples each of dimension D.
- y: A numpy array of shape (N,) containing training labels; y[i] = c
means that X[i] has label 0 <= c < C for C classes.
- learning_rate: (float) learning rate for optimization.
- reg: (float) regularization strength.
- num_iters: (integer) number of steps to take when optimizing
- batch_size: (integer) number of training examples to use at each step.
- verbose: (boolean) If true, print progress during optimization.
Outputs:
A list containing the value of the loss function at each training iteration.
"""
num_train, dim = X.shape
num_classes = np.max(y) + 1 # assume y takes values 0...K-1 where K is number of classes
if self.W is None:
# lazily initialize W
self.W = 0.001 * np.random.randn(dim, num_classes)
# Run stochastic gradient descent to optimize W
loss_history = []
for it in xrange(num_iters):
X_batch = None
y_batch = None
#########################################################################
# TODO: #
# Sample batch_size elements from the training data and their #
# corresponding labels to use in this round of gradient descent. #
# Store the data in X_batch and their corresponding labels in #
# y_batch; after sampling X_batch should have shape (dim, batch_size) #
# and y_batch should have shape (batch_size,) #
# #
# Hint: Use np.random.choice to generate indices. Sampling with #
# replacement is faster than sampling without replacement.
#有放回的抽样比无放回的抽样更快
#########################################################################
choice = np.random.choice(num_train, batch_size, replace=True)
X_batch = X[choice]
y_batch = y[choice]
#########################################################################
# END OF YOUR CODE #
#########################################################################
# evaluate loss and gradient
loss, grad = self.loss(X_batch, y_batch, reg)
loss_history.append(loss)
# perform parameter update
#########################################################################
# TODO: #
# Update the weights using the gradient and the learning rate. #
#########################################################################
self.W -= learning_rate * grad
#########################################################################
# END OF YOUR CODE #
#########################################################################
if verbose and it % 100 == 0:
print('iteration %d / %d: loss %f' % (it, num_iters, loss))
return loss_history
def predict(self, X):
"""
Use the trained weights of this linear classifier to predict labels for
data points.
Inputs:
- X: A numpy array of shape (N, D) containing training data; there are N
training samples each of dimension D.
Returns:
- y_pred: Predicted labels for the data in X. y_pred is a 1-dimensional
array of length N, and each element is an integer giving the predicted
class.
"""
y_pred = np.zeros(X.shape[0])
###########################################################################
# TODO: #
# Implement this method. Store the predicted labels in y_pred. #
###########################################################################
scores = np.dot(X, self.W)
y_pred = np.argmax(scores, axis=1)
###########################################################################
# END OF YOUR CODE #
###########################################################################
return y_pred
def loss(self, X_batch, y_batch, reg):
"""
Compute the loss function and its derivative.
Subclasses will override this.
Inputs:
- X_batch: A numpy array of shape (N, D) containing a minibatch of N
data points; each point has dimension D.
- y_batch: A numpy array of shape (N,) containing labels for the minibatch.
- reg: (float) regularization strength.
Returns: A tuple containing:
- loss as a single float
- gradient with respect to self.W; an array of the same shape as W
"""
pass
class LinearSVM(LinearClassifier):
""" A subclass that uses the Multiclass SVM loss function """
def loss(self, X_batch, y_batch, reg):
return svm_loss_vectorized(self.W, X_batch, y_batch, reg)
class Softmax(LinearClassifier):
""" A subclass that uses the Softmax + Cross-entropy loss function """
def loss(self, X_batch, y_batch, reg):
return softmax_loss_vectorized(self.W, X_batch, y_batch, reg)data_preprocessing&test
0均值
mean_image = np.mean(X_train, axis=0)
X_train -= mean_image
X_val -= mean_image
X_test -= mean_image
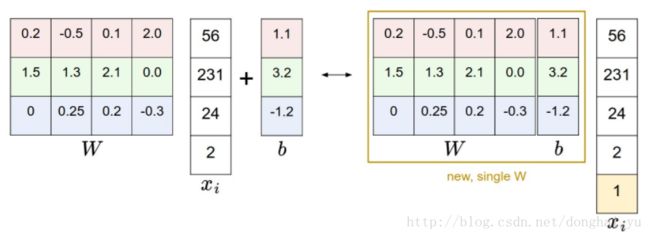
X_dev -= mean_imageX增加全为1的一列,使得W增加一行(bias项),如此训练时只用考虑W
X_train = np.hstack([X_train, np.ones((X_train.shape[0], 1))])
X_val = np.hstack([X_val, np.ones((X_val.shape[0], 1))])
X_test = np.hstack([X_test, np.ones((X_test.shape[0], 1))])
X_dev = np.hstack([X_dev, np.ones((X_dev.shape[0], 1))])
以正态分布初始化W,预期loss应为C-1 = 10-1 = 9
from cs231n.classifiers.linear_svm import svm_loss_naive
import time
# generate a random SVM weight matrix of small numbers
W = np.random.randn(3073, 10) * 0.0001
loss, grad = svm_loss_naive(W, X_dev, y_dev, 0.000005)
print('loss: %f' % (loss, ))loss: 9.254977##SVM正常工作
调参 tune hyperparameters(regularization strength、learning rate)
遍历两个超参数的候选范围(two loops),每次都将SVM实例化利用当前参数训练和预测,利用打擂台的方式找到最高的正确率以及相对应的svm,也可根据输出的accuracy将超参数的候选范围进一步缩小,找到最优的参数(开始时选择较小的迭代次数可以节省时间,确定一个更小的范围后可以再考虑使用更大的迭代次数)
# Use the validation set to tune hyperparameters (regularization strength and
# learning rate). You should experiment with different ranges for the learning
# rates and regularization strengths; if you are careful you should be able to
# get a classification accuracy of about 0.4 on the validation set.
learning_rates = [1e-7, 5e-5]
regularization_strengths = [2.5e4, 5e4]
# results is dictionary mapping tuples of the form
# (learning_rate, regularization_strength) to tuples of the form
# (training_accuracy, validation_accuracy). The accuracy is simply the fraction
# of data points that are correctly classified.
results = {}
best_val = -1 # The highest validation accuracy that we have seen so far.
best_svm = None # The LinearSVM object that achieved the highest validation rate.
################################################################################
# TODO: #
# Write code that chooses the best hyperparameters by tuning on the validation #
# set. For each combination of hyperparameters, train a linear SVM on the #
# training set, compute its accuracy on the training and validation sets, and #
# store these numbers in the results dictionary. In addition, store the best #
# validation accuracy in best_val and the LinearSVM object that achieves this #
# accuracy in best_svm. #
# #
# Hint: You should use a small value for num_iters as you develop your #
# validation code so that the SVMs don't take much time to train; once you are #
# confident that your validation code works, you should rerun the validation #
# code with a larger value for num_iters. #
################################################################################
for lr in learning_rates:
for reg in regularization_strengths:
svm = LinearSVM()
svm.train(X_train, y_train, lr, reg, num_iters=2000, verbose=False)
y_train_pred = svm.predict(X_train)
y_val_pred = svm.predict(X_val)
training_accuracies = np.mean(y_train == y_train_pred)
validation_accuracies = np.mean(y_val == y_val_pred)
results[(lr, reg)] = (training_accuracies, validation_accuracies)
if validation_accuracies > best_val:
best_val = validation_accuracies
best_svm = svm
################################################################################
# END OF YOUR CODE #
################################################################################
# Print out results.
for lr, reg in sorted(results):
train_accuracy, val_accuracy = results[(lr, reg)]
print('lr %e reg %e train accuracy: %f val accuracy: %f' % (
lr, reg, train_accuracy, val_accuracy))
print('best validation accuracy achieved during cross-validation: %f' % best_val)output
一番调参后,得到accuracy超过40%的W,算是把这个作业给完成了