（精）广东工业大学《数据可视化技术》 2018实验报告

（精）广东工业大学《数据可视化技术》 2018实验报告

前言：此为《数据可视化设计》课程实验报告（个人重现 + 重制版）。鉴于实验时发现 实验指导书中 存在 排版混乱、图片不清晰、WPS与Offic的截图混用、代码 中英文标点混用、缺少效果图等问题，同时数据源分散于多个零散文件中，整个实验过程十分痛苦。。。故重制此报告，增删完善汇总，以便日后回看，欢迎大家交流学习。

报告中所使用的软件版本：Excel 2016、MATLAB R2018a、Tableau 2018.1.0。

实验一 Excel数据可视化

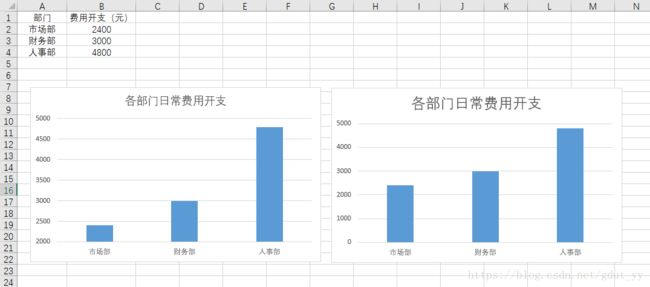
1.用Excel绘制直方图

直方图：又称质量分布图、柱状图，是一种统计报告图，也是表示资料变化情况的主要工具。直方图由一系列高度不等的纵向条纹或线段表示数据分布的情况，一般用横轴表示数据类型，纵轴表示分布情况。

实验数据和结果

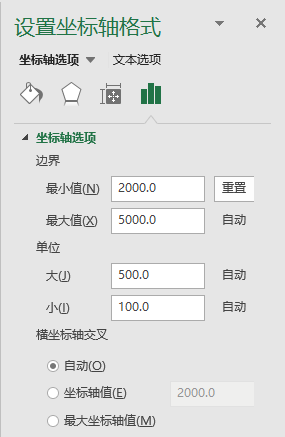
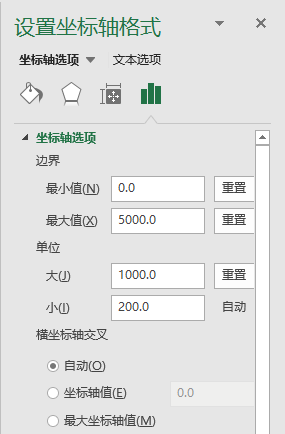
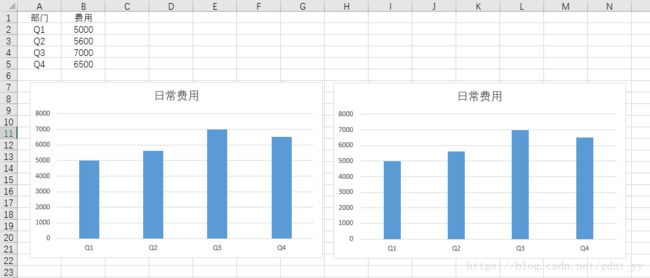
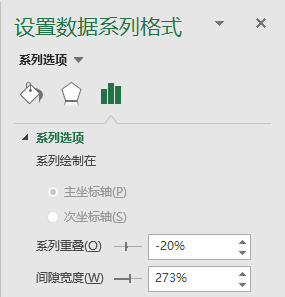
（设置数据系列的间距等）

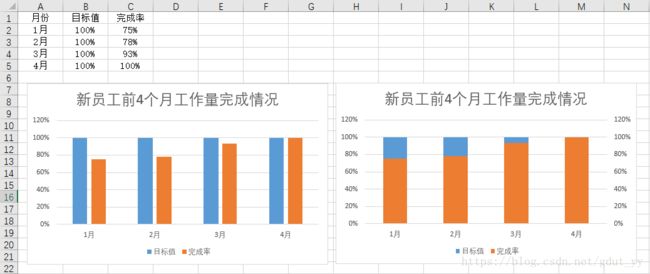
2.绘制百分比柱形堆积图

（PS：数据系列绘制选择次坐标轴）

3.折线图

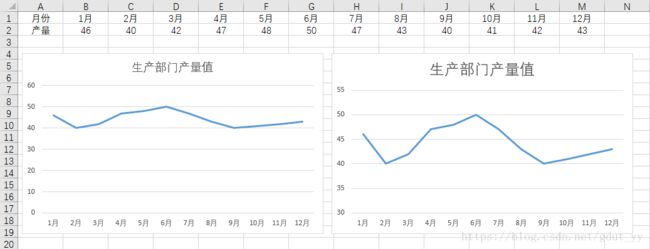
3.1 单折线

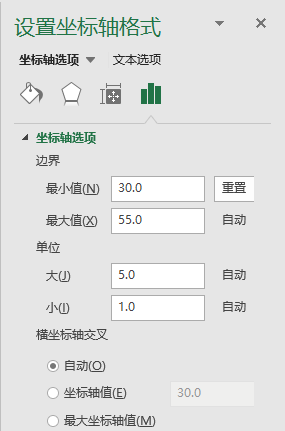
单击Y轴坐标，打开坐标轴格式窗格，在“坐标轴选项”下输入边界最小值“30”，边界最大值“50”，然后输入主要单位值“5”，结果如图所示。

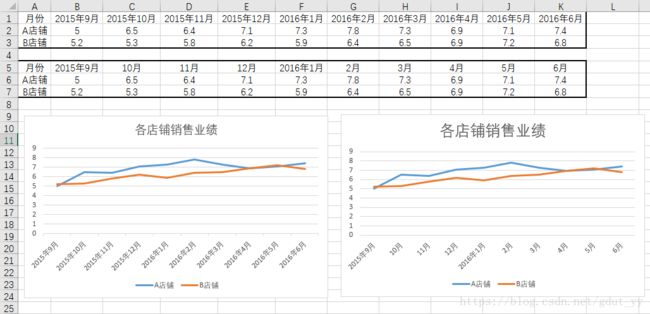
3.2 双折线图

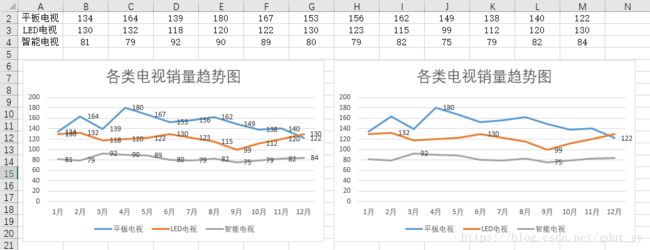
3.3 三折线并加突出显示折线图中的数据点

（加数据标签） / （删除不需要显示的数据标签）

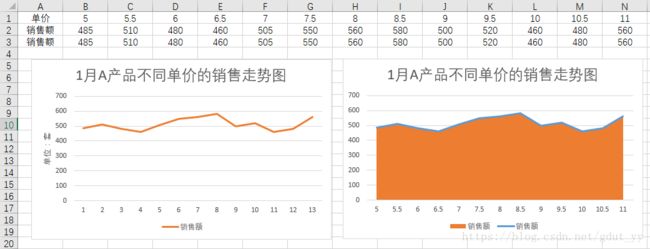
3.4 折线图+面积图

4.圆饼图

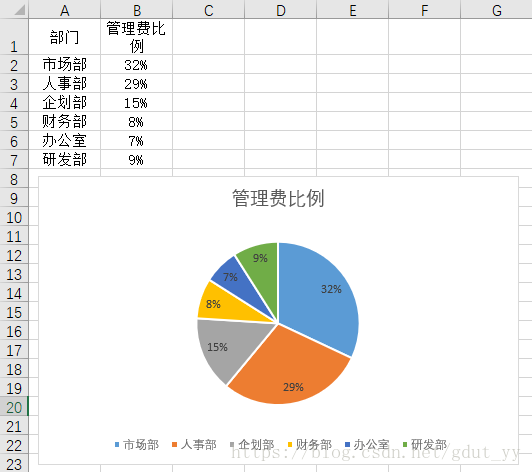
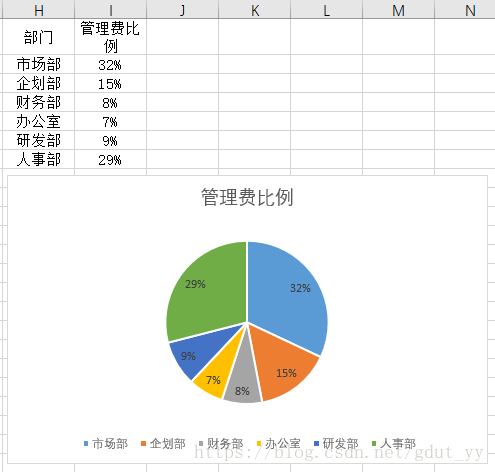
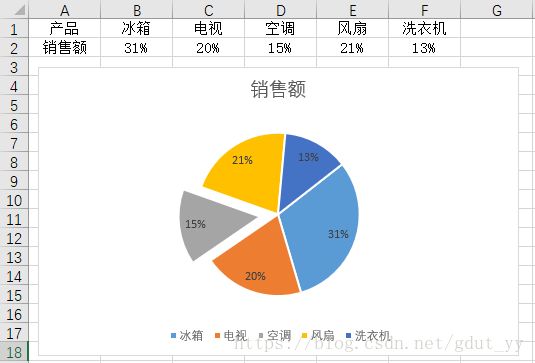
4.1 圆饼图

一般而言，圆饼图的切片分布一般是将数据较大的两个扇区设置在水平方向的左右两侧。因此，可通过更改数据源的排序顺序改变圆饼图切片的分布位置外，还可以对圆饼图切片进行旋转，使圆饼图的两个较大扇区分布在左右两侧。如

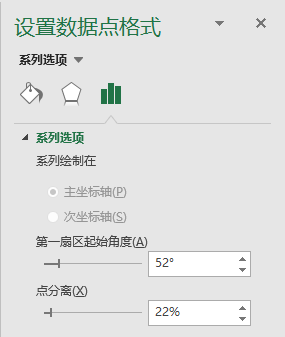
4.2 分离圆饼图

(双击圆饼图打开“设置数据系列格式”窗格，再单击需要被强调的扇区（系列为“空调”），然后在“系列选项”组下设置“点爆炸型”的百分比值为“22%”，即将所选中的扇区单独分离出来。由于分离的扇区显示在图表下方，需要调整“第一扇区起始角度”值“52”来改变扇区位置，使其显示在图表的左边区域）

5.散点图

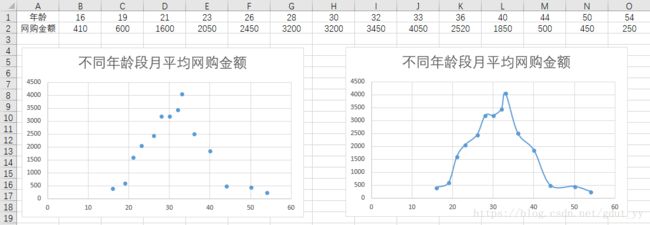
5.1 平滑线联系散点图

---

实验二 Matlab数据可视化（一）

1.Matlab离散数据可视化

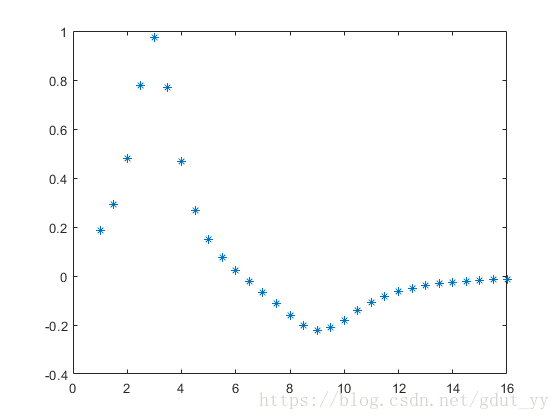
绘制离散函数 y=1(n−3)2+1+1(n−9)2+4 y = 1 ( n − 3 ) 2 + 1 + 1 ( n − 9 ) 2 + 4 的图形，其中自变量的取值范围是(0,16)的整数。

n=1:0.5:16;
y=1./((n-3).^2+1)-1./((n-9).^2+4);
plot(n,y,'*')

思考：根据如下指令，试着修改颜色、线型、

plot(x, y, 'CLM');  %控制颜色,线形状,点

C 代表颜色(Colors), L 代表曲线的格式(Line Styles), M 代表曲线所用的线标(Markers)。

线型 线方式： - 实线； : 点线； -. 虚点线； - - 波折线。

线型 点方式： . 圆点； + 加号； * 星号； x x形； o 小圆。

颜色： y黄； r红； g绿； b蓝； w白； k黑； m紫； c青。

2. 二维曲线绘制实验

2.1 设计实验演示验证plot

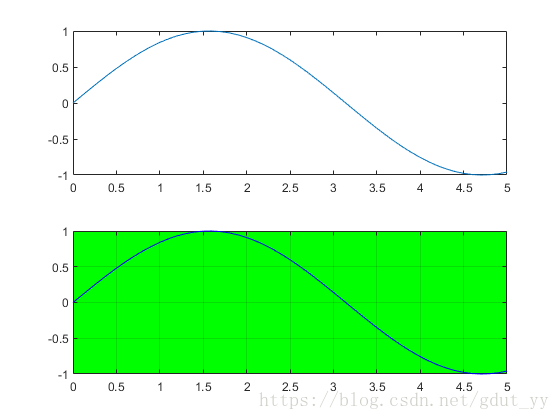
设置三个函数y,z,h均以x作为变量,验证函数plot,subplot,set, axis,并使用grid on为图形加网格, box on加边框线。

x=0:0.1:5; 
y=sin(x); 
z=cos(x); 
h=tan(x);  
subplot(2,1,1);
plot(x,y); 
subplot(2,1,2); 
plot(x,z);  
axis([0 4 0 20]); 
h=plot(x,y); 
set(h,'color','b');  
set(gca,'XGrid','on','YGrid','off'); 
set(gca,'color','g');
grid on
box on

思考：使用Matlab help指令（或百度），了解subplot，set,axis的用法。

例如：matlab中subplot(m,n,p)可以在一个figure中画m×n个子图，p可以指定子图的位置，一般情况下p为单个数字，p为向量时可以合并多个子图为一个子图。

http://blog.csdn.net/gsls200808/article/details/45870911（不同的子图合并方式）

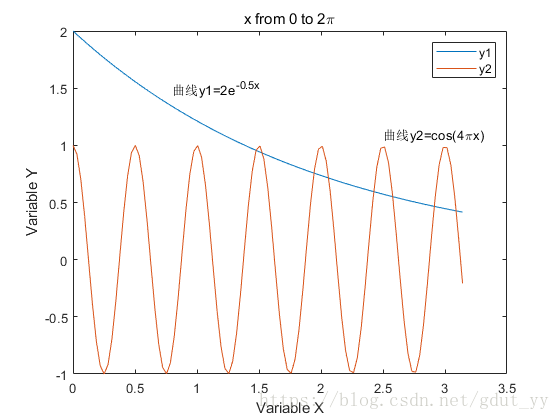
2.2 设计函数y1=2e-0.5x和y2=cos(4πx)绘制其曲线，为其添加title(图形名称) ，label(x轴说明)，ylabel(y轴说明)，text(x,y,图形说明)，legend(图例1,图例2,…)。

x=0:pi/100:1*pi;
y1=2*exp(-0.5*x);
y2=cos(4*pi*x);
plot(x,y1,x,y2)
title('x from 0 to 2{\pi}');             
xlabel('Variable X');                 
ylabel('Variable Y');                  
text(0.8,1.5,'曲线y1=2e^{-0.5x}');      
text(2.5,1.1,'曲线y2=cos(4{\pi}x)');
legend('y1','y2')  

思考：使用Matlab菜单，直接进行title，legend的修改。使用Matlab help指令（或百度），了解text的用法。

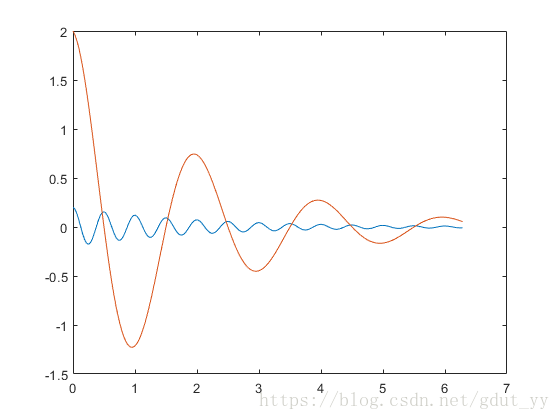
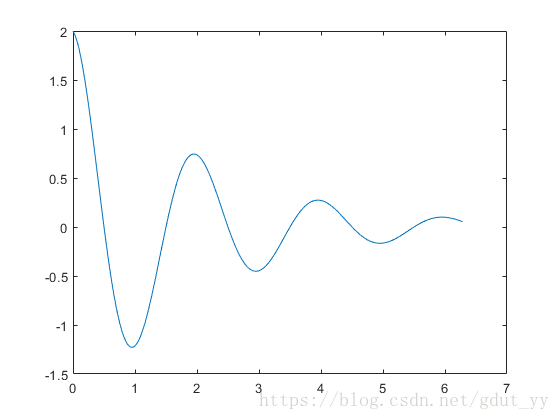
2.3 设计函数y1=0.2e-0.5xcos(4πx) 和y2=2e-0.5xcos(πx)，并在同一坐标内绘制曲线，验证hold on/off命令的切换。

x=0:pi/100:2*pi;
y1=0.2*exp(-0.5*x).*cos(4*pi*x);
plot(x,y1)
hold on
y2=2*exp(-0.5*x).*cos(pi*x);
plot(x,y2);
hold off

思考：去掉hold on/hold off结果的区别？

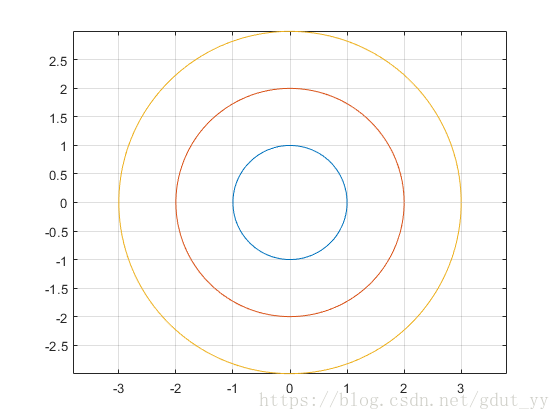
2.4 设计函数x=exp(i*t)和y=[x;2*x;3*x]’在同一坐标中，绘制3个同心圆，并加坐标控制，并使用 grid on加网格线， box on加坐标边框，axis equal使坐标轴采用等刻度。

t=0:0.01:2*pi;
x=exp(i*t);
y=[x;2*x;3*x]';
plot(y)
grid on;            %加网格线
box on;             %加坐标边框
axis equal          %坐标轴采用等刻度

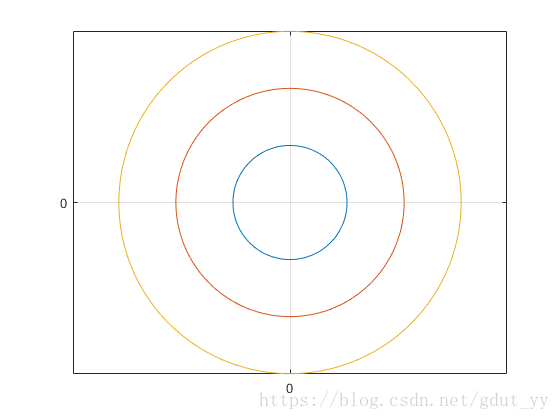
思考：grid on和grid off进行网格线的控制，如何进行网格线坐标的控制？（采用set命令 ，例如set(gca,’YTickMode’,’manual’,’YTick’,[-16384,0,16384])
set(gca,’XTickMode’,’manual’,’XTick’,[-21846,-10922,0,10922,21846])）

set(gca,'YTickMode','manual','YTick',[-16384,0,16384])
set(gca,'XTickMode','manual','XTick',[-21846,-10922,0,10922,21846])

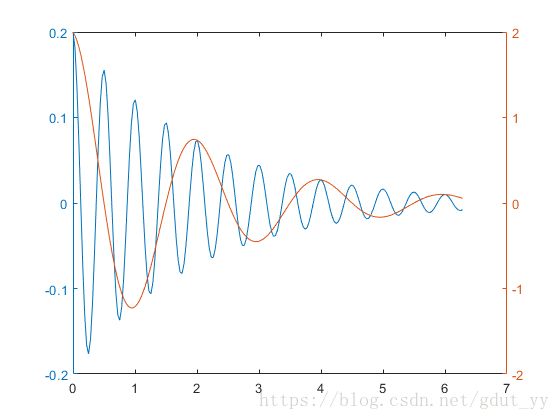
2.5 设计函数y1=0.2e-0.5xcos(4πx) 和y2=2e-0.5xcos(πx)，以不同标度在同一坐标内绘制曲线，验证函数plotyy。

x=0:pi/100:2*pi;
y1=0.2*exp(-0.5*x).*cos(4*pi*x);
y2=2*exp(-0.5*x).*cos(pi*x);
plotyy(x,y1,x,y2);

思考：plotyy为双纵坐标绘图,基本用法为plotyy(x1,y1,x2,y2)，具体用法可参见http://blog.sciencenet.cn/blog-427568-719786.html

---

实验三 Matlab数据可视化（二）

1. 三维曲线绘制实验

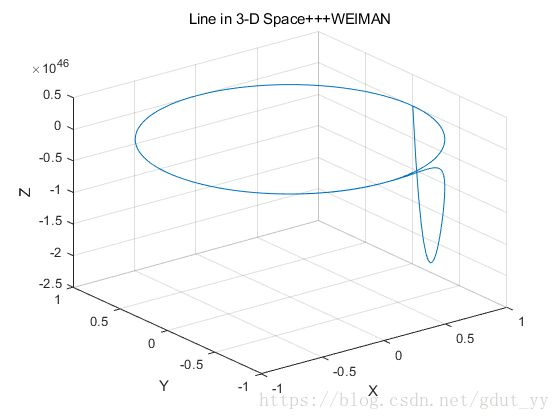
1.1 设计函数y=sin(t)， x=cos(t)， z=(t+1).^t.*sin(t).*cos(t)，并使用plot3函数绘制这三个函数的曲线。

t=0:pi/100:10*pi;
y=sin(t);
x=cos(t);
z=(t+1).^t.*sin(t).*cos(t);
plot3(x,y,z);
title('Line in 3-D Space+++WEIMAN');
xlabel('X');ylabel('Y');zlabel('Z');
grid on;

思考：plot3函数的用法？plot3(x1,y1,z1) 其中x1,y1,z1为相同维数的向量，分别存储各个点坐标。对曲线属性的设置和plot一样，请参考其他设置。当然对图形属性的设置也一样。具体可使用help plot3查看Matlab帮助。

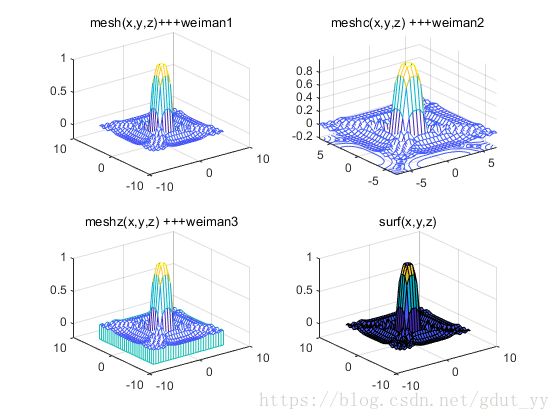
1.2 设计函数z=sin(x+sin(y))-x/10;，分别绘制带等高线的三维网格曲面函数meshc和带底座的三维网格曲面函数meshz。并使用函数surf绘制该函数图像

[x,y]=meshgrid(-7:0.5:7);
z=sin(sqrt(x.^4+y.^4))./sqrt(x.^4+y.^4+eps);
subplot(2,2,1);
mesh(x,y,z);
title('mesh(x,y,z)+++weiman1')
subplot(2,2,2);
meshc(x,y,z);
title('meshc(x,y,z) +++weiman2')
subplot(2,2,3);
meshz(x,y,z)
title('meshz(x,y,z) +++weiman3')
subplot(2,2,4);
surf(x,y,z);
title('surf(x,y,z)');

思考：meshc，meshz，surf函数的用法？

1.3 三维图形编辑（精细控制）实验：设计实验演示验证用view、rotate、colordef、colormap、shading、light、lighting、material、surfl等函数对三维图形进行精细控制的方法。

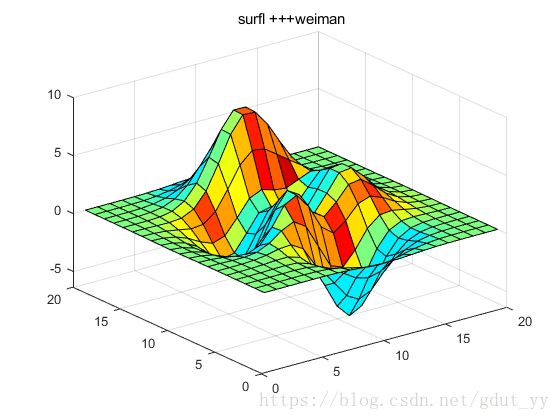
函数surfl功能

z=peaks(20); 
colordef white ; 
colormap jet; 
shading interp; 
surfl(z)
title(' surfl +++weiman')

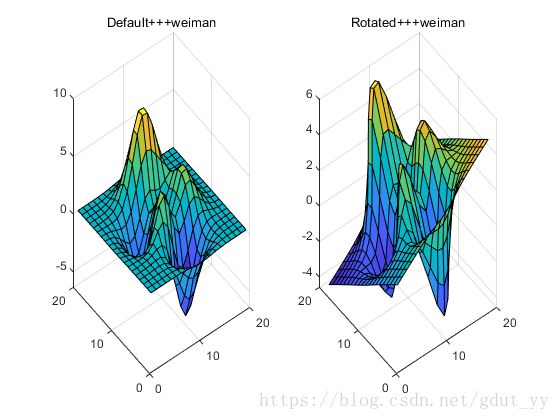
函数rotate功能

z=peaks(20);  
subplot(1,2,1);surf(z);title('Default+++weiman');           
subplot(1,2,2);h=surf(z);title('Rotated+++weiman'); 
rotate(h,[-2,-2,0],20,[2,2,0]); 

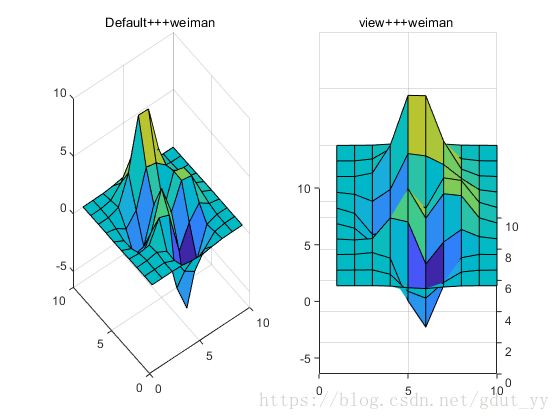
函数view功能

z=peaks(10);  
subplot(1,2,1);surf(z);title('Default+++weiman '); 
subplot(1,2,2);  
subplot(1,2,2);h=surf(z);title('view+++weiman '); 
view(0,40);  

2 统计图绘制实验

2.1 设计实验演示验证面域图（area）

x=-2:2
Y=[3,8,9,4,1;6,3,5,2,7;5,4,3,8,6]   %(3*5)的Y数组的
CS=flipud(cumsum(Y))
area(x',Y',0)
legend('因素A','因素B','因素C')
grid on,
colormap('jet')
title('area+++weiman')

思考：自己提供数据，画出面域图？

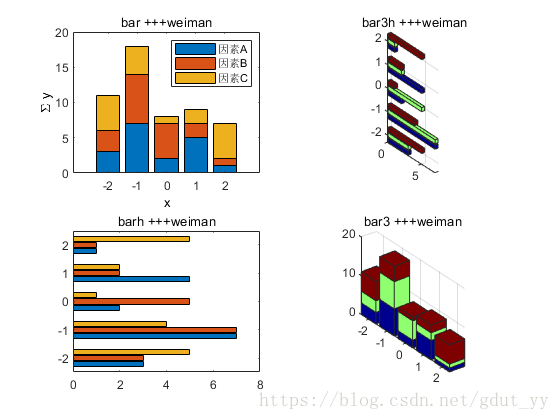
2.2 设计实验演示验证直方图（bar、barh、bar3、bar3h）

x=-2:2;
Y=[3,7,2,5,1;3,7,5,2,1;5,4,1,2,5];
subplot(2,2,1)
bar(x',Y','stacked')
title('bar +++weiman')
xlabel('x'),ylabel('\Sigma y'), colormap('jet')
legend('因素A','因素B','因素C')
subplot(2,2,2)
bar3h(x',Y','grouped')
title(' bar3h +++weiman')
subplot(2,2,4)
bar3(x',Y','stacked')
title('bar3 +++weiman')
subplot(2,2,3)
barh(x',Y', 'grouped')
title('barh +++weiman')

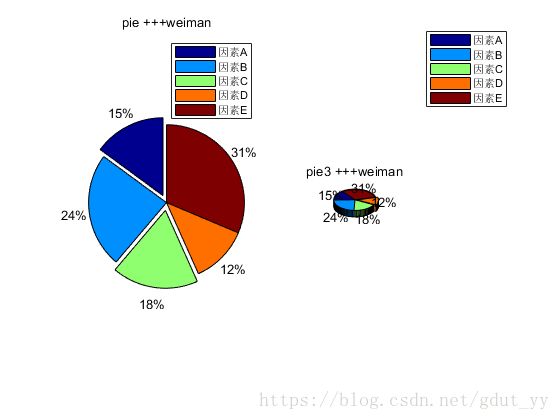
2.3 饼图（pie、pie3）

a=[1,1.6,1.2,0.8,2.1];
subplot(1,2,1)
pie(a,[1 0 1 0 0])
axis equal
title('pie +++weiman')
legend('因素A','因素B','因素C','因素D','因素E')
subplot(1,2,2)
pie3(a,double(a==min(a)))
colormap(jet)
title('pie3 +++weiman')
legend('因素A','因素B','因素C','因素D','因素E')

2.4 散点图（scatter、scatter3、plotmatrix）

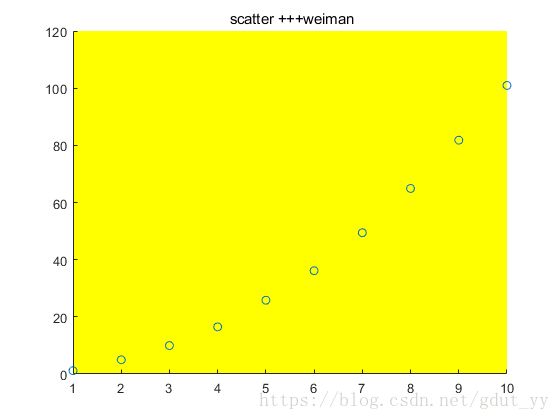
2.4.1 scatter(X,Y)

X = [1:10];
Y = X.^2 + rand(size(X));
scatter(X, Y)
set(gca,'color','y');
title(' scatter +++weiman')

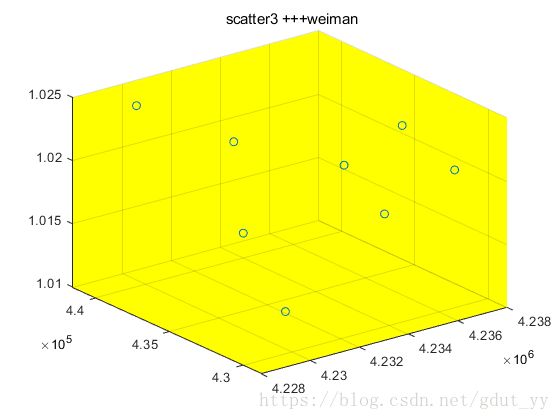
2.4.2 函数scatter3

x=[4229042.63 4230585.02 4231384.96 4231773.63 4233028.58 4233296.71 4235869.68 4236288.29];
y=[431695.4 441585.8 432745.6 436933.7 428734.4 431946.3 428705.0 432999.5];
z=[1.019 1.023 1.011 1.022 1.020 1.022 1.022 1.023];
scatter3(x,y,z)
set(gca,'color','y');
title(' scatter3 +++weiman')

注：x,y,z必须是等长度的数对（即三个等长的矢量）

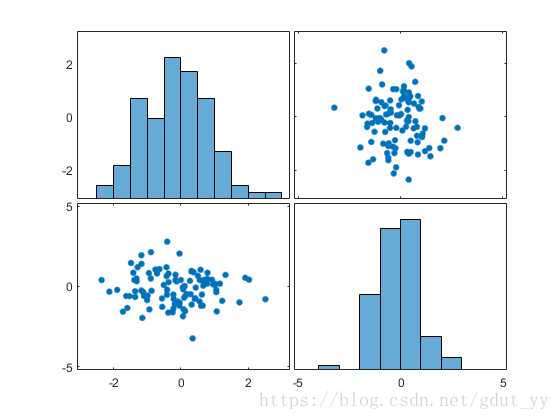
2.4.3 Plotmatrix函数

x=randn(100,2)
plotmatrix(x)

3.动画绘制实验：设计实验演示验证getframe与movie相结合绘制动画的方法。

%影片生成例子: 旋转一个三维表面绘图
[X, Y, Z]=peaks(50);            %创建山峰图形数据
surfl(X, Y, Z)                  %绘制带光照的表面
axis([-10 10 -10 10 -10 10])    %限制绘图范围
axis vis3d off                  %三维坐标修正,关闭坐标轴箭头
axis equal                      %等比例显示三维坐标
shading interp                  %加个影子美化
colormap(copper)                %着色为铜色
for i=1:360                     %旋转山峰,从1到360度,每一度捕捉一帧
view(-37.5+i,30)                %从水平-37.5+i度,垂直30度的方向看山  
m(i)=getframe;                  %每从一个角度看到一张图像(帧),就存储到m
end                             %每次看完,水平转动1度,直到1周360度;
cla                             %为播放影片清除坐标
movie(m)                        %把刚才存到m里的图像连续播放一遍,就是影片了.

---

实验四 Matlab数据可视化（三）

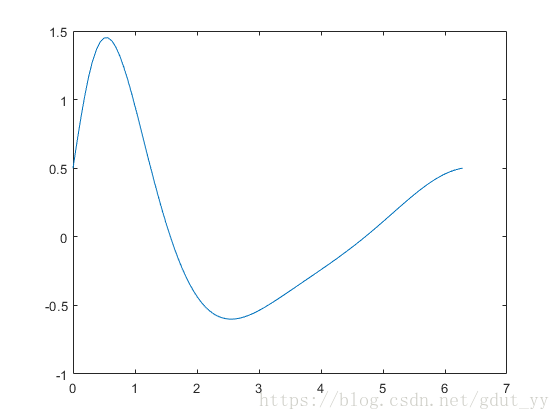
1.设 y=[0.5+3sinx1+x2]cosx y = [ 0.5 + 3 sin ⁡ x 1 + x 2 ] cos ⁡ x ，在 x=0~2π区间取 101 点，绘制函数的曲线。

解：M 文件如下：

clc; 
x=linspace(0,2*pi,101); 
y=(0.5+3*sin(x)./(1+x.^2)).*cos(x); 
plot(x,y) 

运行结果有：

2.已知y1=x^2，y2=cos(2x)，y3=y1×y2，完成下列操作：

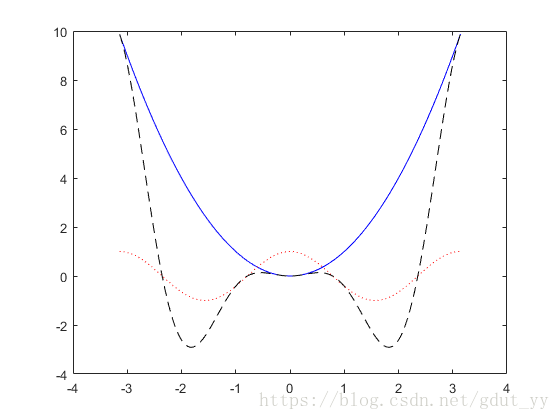
(1) 在同一坐标系下用不同的颜色和线型绘制三条曲线。

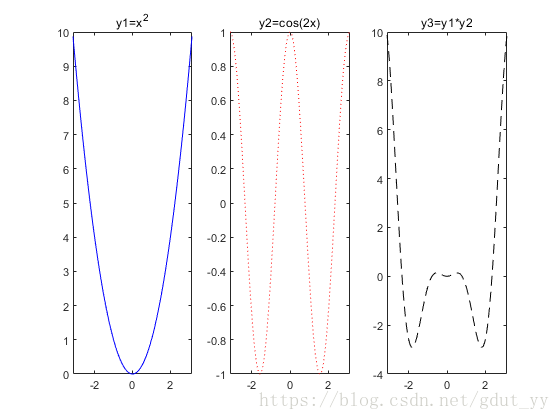
(2) 以子图形式绘制三条曲线。

(3) 分别用条形图、阶梯图、杆图和填充图绘制三条曲线。

解：

（1） M 文件：

clc; 
x=-pi:pi/100:pi; 
y1=x.^2; 
y2=cos(2*x); 
y3=y1.*y2; 
plot(x,y1,'b-',x,y2,'r:',x,y3,'k--') 

运行结果：

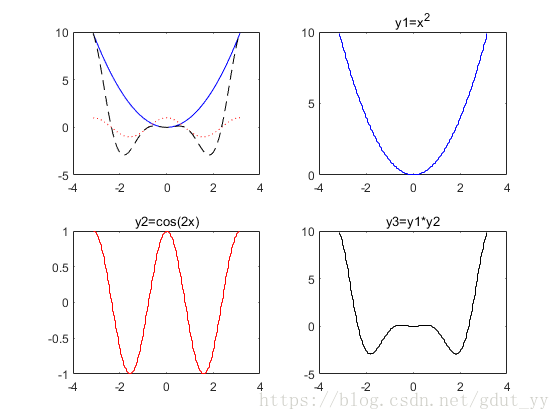
（2）M 文件：

clc; 
x=-pi:pi/100:pi; 
y1=x.^2; 
y2=cos(2*x); 
y3=y1.*y2; 
subplot(1,3,1); 
plot(x,y1,'b-'); 
title('y1=x^2'); 
subplot(1,3,2); 
plot(x,y2,'r:'); 
title('y2=cos(2x)'); 
subplot(1,3,3); 
plot(x,y3,'k--'); 
title('y3=y1*y2'); 

运行结果：

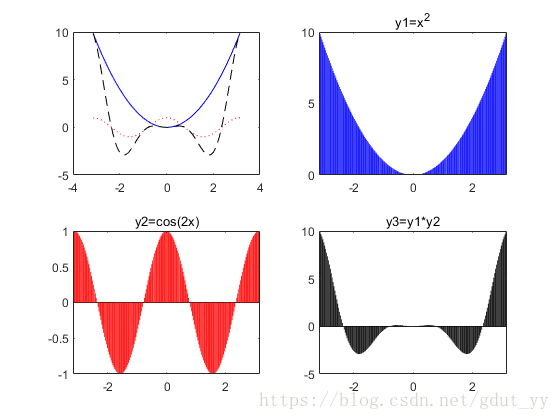
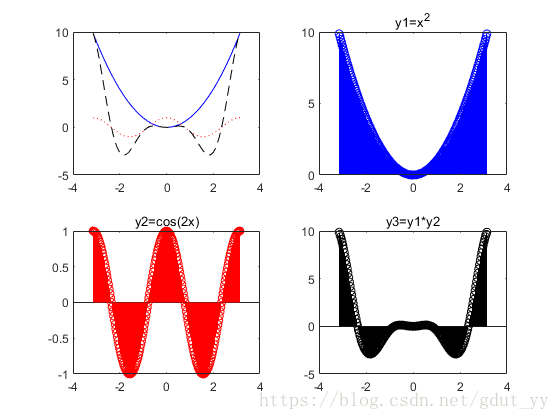
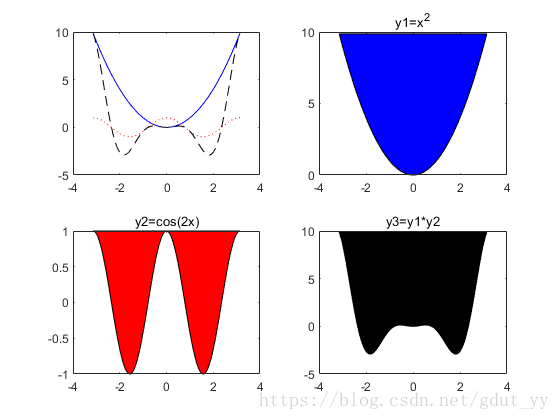
（3）M 文件：

clc; 
x=-pi:pi/100:pi; 
y1=x.^2; 
y2=cos(2*x); 
y3=y1.*y2; 
subplot(2,2,1); 
plot(x,y1,'b-',x,y2,'r:',x,y3,'k--'); 
subplot(2,2,2); 
bar(x,y1,'b'); 
title('y1=x^2'); 
subplot(2,2,3); 
bar(x,y2,'r');  
title('y2=cos(2x)'); 
subplot(2,2,4); 
bar(x,y3,'k'); 
title('y3=y1*y2');  

由上面的 M 文件，只要依次将“bar”改为“stairs”、“stem”、“fill”,再适当更改区间取的点数，运行程序即可，即有下面的结果：

3.

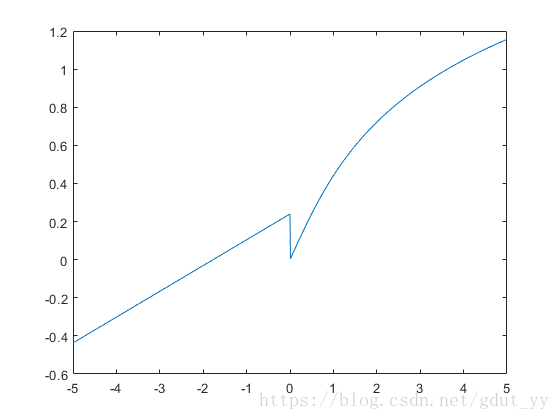
已知

y=⎧⎩⎨⎪⎪x+π√e212ln(x+1+x2−−−−−√)x≤0x>0 y = { x + π e 2 x ≤ 0 1 2 ln ⁡ ( x + 1 + x 2 ) x > 0

在-5≤x≤5 区间绘制函数曲线。

解：M 文件：

clc; 
x=-5:0.01:5; 
y=(x+sqrt(pi))/(exp(2)).*(x<=0)+0.5*log(x+sqrt(1+x.^2)).*(x>0); 
plot(x,y)  

运行结果：

由图可看出，函数在零点不连续。

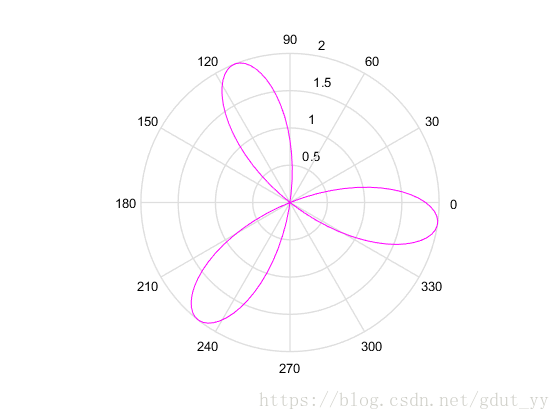
4.绘制极坐标曲线ρ=asin(b+nθ)，并分析参数 a、b、n 对曲线形状的影响。

解：M 文件如下：

clc; 
theta=0:pi/100:2*pi; 
a=input('输入 a='); 
b=input('输入 b='); 
n=input('输入 n='); 
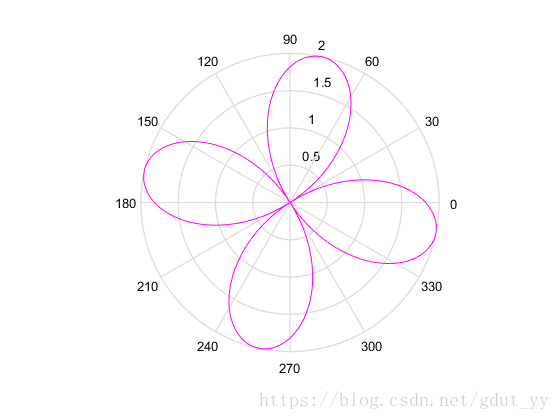
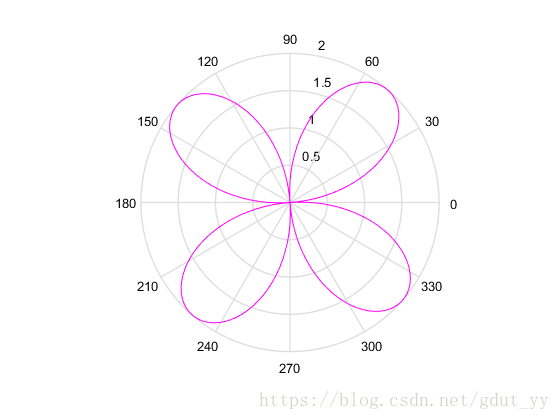
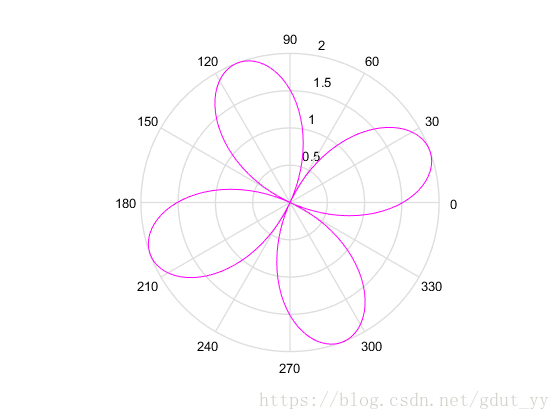
rho=a*sin(b+n*theta); 
polar(theta,rho,'m') 

采用控制变量法的办法，固定两个参数，变动第三个参数观察输出图象的变化。

▲a=n=2,b=2

▲a=n=2,b=3

▲a=n=2,b=4

---

▲a=b=2,n=2

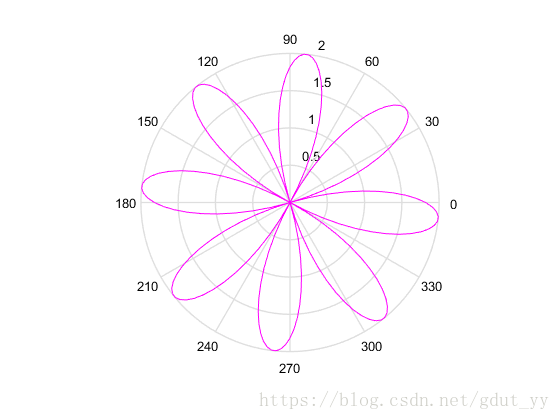
▲a=b=2,n=3

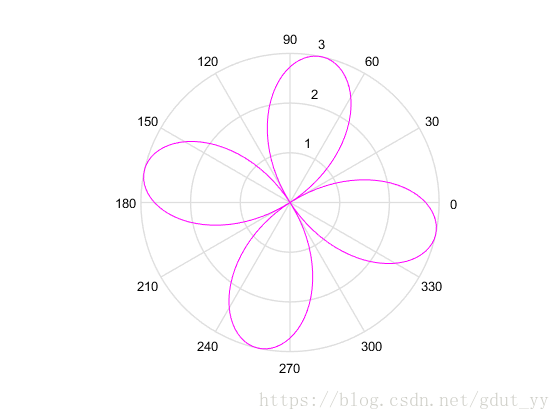
▲a=b=2,n=4

---

▲b=n=2,a=2

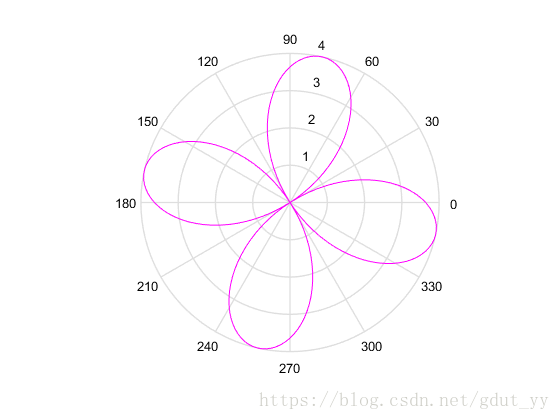
▲b=n=2,a=3

▲b=n=2,a=4

分析结果：由这 9 个图（其实只有7个）知道，

当 a,n 固定时，图形的形状也就固定了，b 只影响图形的旋转的角度;

当 a,b 固定时，n 只影响图形的扇形数，特别地，当 n 是奇数时，扇叶数就是 n,当是偶数时，扇叶数则是 2n 个;

当 b,n 固定时，a 影响的是图形大小，特别地，当 a 是整数时，图形半径大小就是 a。

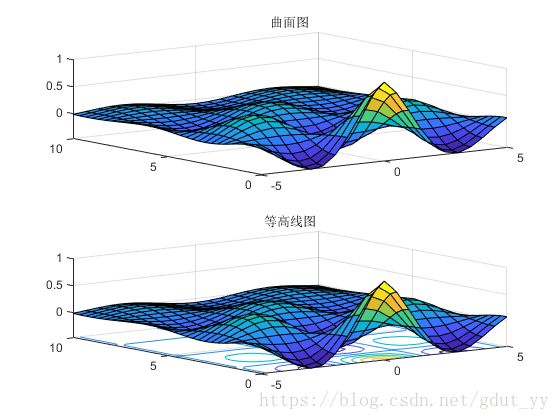
5.绘制函数的曲线图和等高线。

z=cosxcosy e−x2+y24 z = cos ⁡ x cos ⁡ y   e − x 2 + y 2 4

其中 x 的 21 个值均匀分布[-5，5]范围，y 的 31 个值均匀分布在[0，10]，要求使用 subplot(2,1,1)和 subplot(2,1,2)将产生的曲面图和等高线图画在同一个窗口上。

解：M 文件：

clc; 
x=linspace(-5,5,21); 
y=linspace(0,10,31); 
[x,y]=meshgrid(x,y); 
z=cos(x).*cos(y).*exp(-sqrt(x.^2+y.^2)/4); 
subplot(2,1,1); 
surf(x,y,z); 
title('曲面图'); 
subplot(2,1,2); 
surfc(x,y,z); 
title('等高线图');  

运行结果：

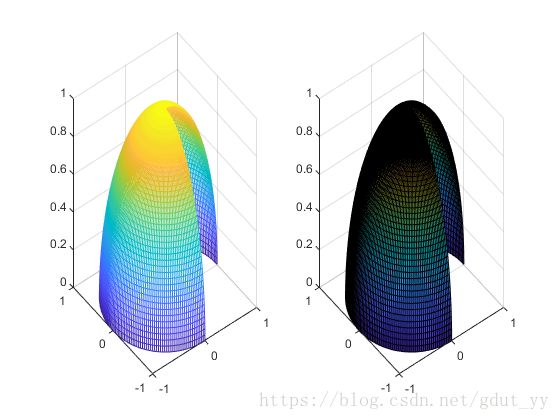
6.绘制曲面图形。

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪x=cosscosty=cosssintz=sins0≤s≤π2,0≤t≤3π2 { x = cos ⁡ s cos ⁡ t y = cos ⁡ s sin ⁡ t 0 ≤ s ≤ π 2 , 0 ≤ t ≤ 3 π 2 z = sin ⁡ s

解：M 文件：

clc; 
s=0:pi/100:pi/2; 
t=0:pi/100:3*pi/2; 
[s,t]=meshgrid(s,t); 
x=cos(s).*cos(t);
y=cos(s).*sin(t); 
z=sin(s); 
subplot(1,2,1); 
mesh(x,y,z); 
subplot(1,2,2); 
surf(x,y,z); 

运行结果有：

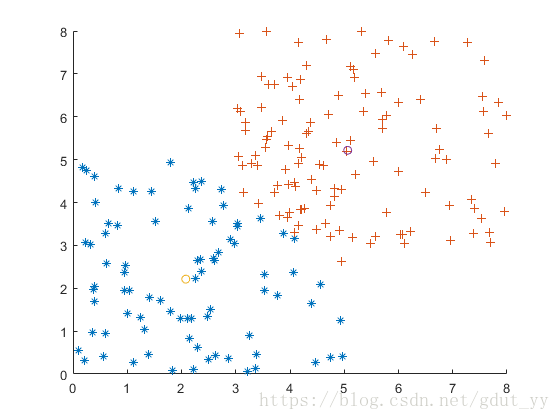
7.Matlab聚类（ K-均值算法，没有中间结果展示。建议增加中间过程观察）

for i=1:100
    x1(i) = rand()*5;       %人为保证差异性
    y1(i) = rand()*5;  
    x2(i) = rand()*5 + 3;   %人为保证差异性
    y2(i) = rand()*5 + 3;
end
x = [x1,x2];
y = [y1,y2];
cities = [x;y];
% plot(cities(1,:),cities(2,:),'*');  %画出来
%%
%------------随机把其中两个点作为初始的聚类中心
num = size(cities,2);       %样本个数
m1 = round(rand()*num);     %随机选取两个当做初始聚类中心
m2 = round(rand()*num);
while m1==m2                %不能相同
    m2 = round(rand()*num);
end                
u1 = cities(:,m1);        
u2 = cities(:,m2);
u_old = [u1,u2];
u_new = [u2,u1];
%%
while u_old ~= u_new   %聚类中心没有变化时退出循环
    u_old = u_new;      %更新聚类中心坐标
    for j=1:num         %对与每一个样本，找到对应的类
        dis1 = norm(cities(:,j)-u1);    %求距离，范数
        dis2 = norm(cities(:,j)-u2);
        if dis1>=dis2  c(j) = 2;        %比较距离，划分类
        else c(j) = 1;
        end
    end
    index1 = find(c==1);        %索引第一类
    index2 = find(c==2);        %...
    sum1 = sum(cities(:,index1),2);     %对第一类中的元素x,y分别求和
    sum2 = sum(cities(:,index2),2);     %...
    u1 = sum1/length(index1);           %对第一类平均，求取新的聚类中心
    u2 = sum2/length(index2);   %...
    u_new = [u1,u2];            %新的聚类中心向量
end
%%
hold on,plot(cities(1,index1),cities(2,index1),'*');    %画出来
hold on,plot(cities(1,index2),cities(2,index2),'+');  
hold on,plot(u1(1),u1(2),'o',u2(1),u2(2),'o');
mean = u_new;

---

实验五 数据可视化工具

1.Tableau工具

https://www.tableau.com/zh-cn
下载免费试用版，对照PPT，学习该工具的使用。

2.数说立方

数说立方是数说故事新推出的一款面向数据分析师的在线商业智能产品。最重要的特点是配备百亿级社交数据库，同时支持全网公开数据实时抓取，从数据源端解决分析师难点;另外数说立方搭载了分布式搜索、语义分析、数据可视化三大引擎系统的海量计算平台，实现数据处理“探索式分析”和“秒级响应”的两个核心功能。同时数说立方是数说故事三大主打产品之一，并与其他两大产品数说聚合和数说雷达实现从数据源、数据分析、到数据展示完整的数据解决方案。
https://cube.datastory.com.cn/

3.Power BI

可将你公司的数据转换为丰富的视觉对象，你可以对这些视觉对象进行收集和组织，从而将注意力集中于重要的内容。

https://powerbi.microsoft.com/zh-cn/get-started/

4.线上制图工具 Chartblocks

世界上最简单的统计图生成器应用程序。几分钟内就可设计并共享统计图

http://www.chartblocks.com/en/

5.https://www.zhihu.com/question/19929609/answer/83664437 （超多可视化工具，大家自己选择一个，进行学习）

---

附：（精）Tableau数据可视化设计实验报告