quat的坐标系转换

oculus获取的pose数据包含坐标和四元数信息，但所处的坐标系和CryEngine坐标系不同

oculus坐标系 ：+x向右，+y向上，+z向外（屏幕外）

cryengine坐标系：+x向右，+y向内（屏幕以内），+z向上

所以需要使用Oculus时，获取的相机位置和四元数都需要进行转换。

坐标转换比较好理解：将z轴和y轴对调再取反即可

Vec3 Device::HmdVec3ToWorldVec3(const Vec3 &vec)
{

// 将oculus的y替换到CryEngine的z，将oculus的z取反，替换CryEngine的y
return Vec3(vec.x, -vec.z, vec.y); 
}

// 以下代码来自CryEnginev5

// -------------------------------------------------------------------------

// 四元数转换，需要考虑两方面：

其一，数值和变换的坐标轴对应；

其二，变换的坐标轴正确。

比较费解的就是为什么要旋转坐标系，个人理解为：

第一步将数值对调，只保证了各个分量所在的x、y、z轴的分量值正确，但oculus和CryEngine原来各自坐标系统下的轴不一致，

经过第一步操作后，作用到模型上后，只是将模型旋转的角度正确了，但默认的相机朝向却不同，需要将oculus的相机朝向和

CryEngine的相机朝向统一为相同方向。

Quat Device::HmdQuatToWorldQuat(const Quat &quat)
{
Matrix33 m33(quat);
Vec3     column1 = -quat.GetColumn2(); // 取出四元数的z变换分量，
m33.SetColumn2(m33.GetColumn1()); // 取出四元数的y变换分量，作为CryEngine的z分量
m33.SetColumn1(column1);// 将oculus取反后的z分量，作为CryEngine的y分量
return Quat::CreateRotationX(gf_PI * 0.5f) * Quat(m33); // 将坐标系从oculus坐标系变换到CryEngine坐标系，以便使其相机朝向一致。
}

=====================================================================================================

后补一：

最近又在处理坐标系变换的问题，发现，其实，以上的解说让你很难理解，用解析几何的知识解释就很容易明白：

OpenGL定义坐标系的绕x旋转矩阵：

以上所要解决的问题就是 将坐标系绕x轴向下旋转90度，便得到目标坐标系。

基于以上理论，但要在具体中应用，需要注意：

该矩阵作用的对象应该是 原来的平移和旋转分量，不能通过矩阵相乘来处理，

1、对于平移的变换需要如下操作：

1.1、设 平移 为T（x,y,z,w）,T'为变换后的平移 ,R为绕x轴向前下放旋转90度的矩阵，

T’ = R*T

1.2、对于原来的旋转，如果使用四元数计算，则需要将旋转矩阵作用到旋转轴上，变换旋转轴，

设原来的旋转轴为 A 

A’ = R* A 

用新的旋转角和旋转轴构造新的四元数。

2、最后将旋转和平移相乘，获得最终的变换矩阵。

举例，以下为osg下的一个转换示例：

// 旋转角度
osg::Matrix rotate = osg::Matrix::rotate(osg::DegreesToRadians(-90.0),osg::Vec3(1,0,0));
osg::Matrix oldMat = _mat; // 
osg::Vec3 oldTrans = oldMat.getTrans(); // 获取平移分量
osg::Quat oldQuat = oldMat.getRotate(); // 获取旋转分量
osg::Vec3 newTrans = rotate * oldTrans; // 计算新的平移
osg::Matrix newTransMat = osg::Matrix::translate(newTrans);
// 计算新的旋转
osg::Vec3 axis;
double angle;
oldQuat.getRotate(angle,axis);
osg::Vec3 newAxis = rotate * axis;
osg::Quat newQuat(angle,newAxis);
// 设置给节点
transformNode->setMatrix(osg::Matrix::rotate(newQuat) *  newMat );

===================================================================================================================================

后补二：

     上面的理解总是有些牵强，有经过几番研究，这下才信服：

1、物体从OpenGL坐标系，变换到OSG坐标系，原来的旋转矩阵，不能直接使用。
2、物体从3dmax建模，导出到OpenGL渲染系统下是y轴向上，导出到OSG渲染系统下是z轴向上，就相当模型已经被绕x轴正向旋转了90度。

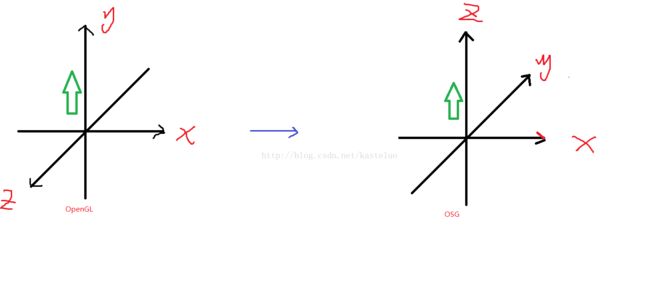
3、模型在OSG坐标系中被加载，原来在OpenGL坐标系下对模型的旋转矩阵，在该系统下就需要进行如下处理：
3.1 乘以一个绕x轴负向90度的旋转矩阵（将模型从z向上，变成y向上）；
3.2 乘以模型在OpenGL坐标系下的旋转矩阵R;
3.3 经过上面两次旋转，模型相当于在OpenGL坐标系下进行了旋转，要让它在OSG下显示正确，需要将OpenGL和OSG坐标系对其， 其实，将OpenGL坐标系
    绕x轴负向旋转90度就得到了OSG坐标系，所以此时，需要再次乘以一个绕x轴负向90度的旋转矩阵

3.4 最终的旋转矩阵为： M = q*R*q-1

3.5 用代码表示:

 

osg::Quat rNeg90(osg::DegreesToRadians(-90.0),osg::Vec3(1,0,0));  
osg::Quat rPos90(osg::DegreesToRadians(90.0),osg::Vec3(1,0,0));  
return rNeg90 * quat * rPos90;
//或 
return rNeg90 * quat * rNeg90.inverse();

  由于

rNeg90 和rPos90 互为逆矩阵，可以替换使用。