SVM学习—Improvements to Platt’s SMO Algorithm
纵观SMO算法，其核心是怎么选择每轮优化的两个拉格朗日乘子，标准的SMO算法是通过判断乘子是否违反原问题的KKT条件来选择待优化乘子的，这里可能有一个问题，回顾原问题的KKT条件：
是否违反它，与这几个因素相关：拉格朗日乘子、样本标记、偏置。的更新依赖于两个优化拉格朗日乘子，这就可能出现这种情况：拉格朗日乘子已经能使目标函数达到最优，而SMO算法本身并不能确定当前由于两个优化拉格朗日乘子计算得到的是否就是使目标函数达到最优的那个，换句话说，对一些本来不违反KKT条件的点，由于上次迭代选择了不合适的，使得它们出现违反KKT条件的情况，导致后续出现一些耗时而无用的搜索，针对标准SMO的缺点，出现了以下几种改进方法，它们同样是通过KKT条件来选择乘子，不同之处为使用对偶问题的KKT条件。
1、通过Maximal Violating Pair选择优化乘子
原问题的对偶问题指的是：
它的拉格朗日方程可以写为：
定义，则对偶问题的KKT条件为：
总结以下可分为3种情况：
分类标记可以取1或-1，按照正类和负类区分指标集，
、 、 、
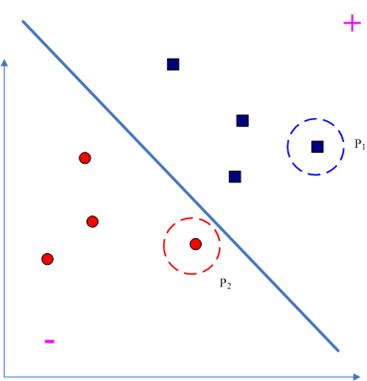
、，如图：
图一
整理一下就得到KKT条件的新形式：
从图上也可以看到，当分类器对全部样本都分类正确的时候，必有：
像标准SMO一样，要精确达到最优值显然也是没必要的，因此这里也需要加个容忍值。引入容忍值后的KKT条件为：
根据前面的说明可以定义“违反对” ： ：
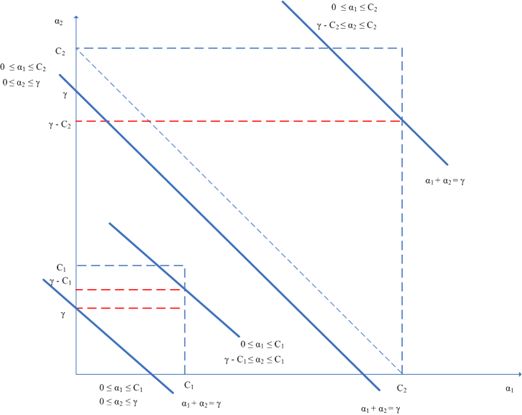
那么我们到底要优化哪两个拉格朗日乘子呢？由“违反对”的定义可知，和差距最大的那两个点最违反KKT条件的，描述为：
于是 就是一个“Maximal Violating Pair，一个示意图如下，其中和就是一对MVP：
2、通过Second Order Information选择优化乘子
不论是通过一阶信息还是二阶信息来选择优化乘子，都是基于以下这个定理：
定理一：如果矩阵为半正定矩阵，当且仅当待优化乘子为“违反对”时，对于SMO类型的算法，其目标函数严格递减(如：)。
First Order Information选择方法我就不介绍了，直接看Second Order Information选择方法：
当选定一个乘子后，另一个乘子选择的条件是使得当前“乘子对”为“违反对”且能使目标函数值最小，在最优化迭代类型方法中非常重要的一个工具就是函数的taylor展开式，优化的过程可以概括为一系列选搜索方向、选搜索步长的过程，对目标函数w展开得：
，
这里d分别为两个待选择乘子的优化方向。于是最小化就变成了：
由优化条件可知：
这样选择乘子的过程就变成了以下优化问题：
总结通过Second Order Information选择优化乘子的方法如下：
1、首先选择一个乘子，条件如下：
2、选择另外一个乘子的过程就是求解的过程，设为第二个乘子，则有：
将条件：
带入有：
于是目标函数在处达到最小值：
用式子表示就是：
当这种情况出现时可以用一个很小的值来代替它，具体可见《A study on SMO-type decomposition methods for support vector machines》一文中“Non-Positive Definite Kernel Matrices”小节。
4、算法实现
将代码加入到了LeftNotEasy的pymining项目中了，可以从http://code.google.com/p/python-data-mining-platform/下载。
几点说明：
1、训练和测试数据格式为：value1 value2 value3 …… valuen，label=+1，数据集放在***.data中，对应的label放在***.labels中，也可以使用libsvm的数据集；
2、分类器目前支持的核为RBF、Linear、Polynomial、Sigmoid、将来支持String Kernel；
3、训练集和测试集的输入支持dense matrix 和 sparse matrix，其中sparse matrix采用CSR表示法；
4、对于不平衡数据的处理一般来说从三个方面入手：
1)、对正例和负例赋予不同的C值，例如正例远少于负例，则正例的C值取得较大，这种方法的缺点是可能会偏离原始数据的概率分布；
2)、对训练集的数据进行预处理即对数量少的样本以某种策略进行采样，增加其数量或者减少数量多的样本，典型的方法如：随机插入法，缺点是可能出现
overfitting，较好的是：Synthetic Minority Over-sampling TEchnique(SMOTE)，其缺点是只能应用在具体的特征空间中，不适合处理那些无法用
特征向量表示的问题，当然增加样本也意味着训练时间可能增加；
3)、基于核函数的不平衡数据处理。
本文就以容易实现为原则，采用第一种方式，配置文件中的节点
和异号且的情形(的情况类似)
和同号的情形
5、算法最耗时的地方是优化乘子的选择和更新一阶导数信息，这两个地方都需要去计算核函数值，而核函数值的计算最终都需要去做内积运算，这就意味着原始空间的维度很高会增加内积运算的时间；对于dense matrix我就直接用numpy的dot了，而sparse matrix采用的是CSR表示法，求它的内积我实验过的方法有三种，第一种不需要额外空间，但时间复杂度为O(nlgn)，第二种需要一个hash表(用dictionary代替了)，时间复杂度为线性，第三种需要一个bitmap(使用BitVector)，时间复杂度也为线性，实际使用中第一种速度最快，我就暂时用它了，应该还有更快的方法，希望高人们能指点一下；另外由于使用dictionary缓存核矩阵，遇到训练数据很大的数据集很容易挂掉，所以在程序中，当dictionary的内存占用达到配置文件的阈值时会将其中相对次要的元素删掉，保留对角线上的内积值。
6、使用psyco
相对于c，python在进行高维度数值计算时表现的会比较差，为了加快数值计算的速度，我使用了psyco来进行加速，它的使用很简单，加两句话就行，用程序测试一下使用psyco之前和之后的表现：
定义一个1164维的向量，代码如下：
1: import time
2: import psyco
3: psyco.full()
4:
5: def dot():
6: vec =[0.0081484941037,0.088244064232,-0.0116517274912,0.0175709303652,-0.0626241393835,-0.0854107365903,-0.0351575090354,0.0380456765128,0.0180095979816,-0.0209914241928,0.163106660981,0.127053320056,-0.0335430235607,-0.0109767864904,0.0709995225815,0.0167076809919,0.027726097262,-0.0311204836595,-0.0259199476295,0.180810035412,-0.0075547491507,-0.0081006110325,0.0270585413405,-0.0148313935713,0.0337146203424,0.0736048267004,-0.182810465676,-0.0267899729122,0.000179219280158,-0.0981396318556,0.0162153149149,0.0158205889243,0.0135732439379,-0.0122793913668,-0.0248816557428,-0.0839578376417,0.00599848509353,0.114707262204,-0.0328007287819,0.0467560652885,0.313179556657,0.024121214556,-0.0553332419857,-0.00684296908044,0.174685776575,0.00418298437096,0.015624947957,-0.0357577181683,-0.0335658241296,-0.0413500938049,0.00890996222676,-0.191520167295,-0.02223857119,-0.00900410728578,-0.00101642281143,-0.0751063838566,-0.00779308778792,-0.0339048097301,-0.29873321989,-0.00751397119331,0.0020689071961,-0.0334433996129,0.0798526578962,-0.00314060942661,0.000994142874497,-0.00385208084616,0.00639638012896,0.00432347948574,-0.0295723516279,-0.0282409806726,-0.243877258982,0.0306503469536,-0.0229985748532,0.0284501391965,-0.198174324275,-0.0179711916393,0.0143267555469,-0.0287066071347,0.000282523969584,0.0616495560776,-0.0172220711262,-0.0687083629936,-0.00370051948645,-0.0219797414557,0.15847905705,0.0354483161821,0.0763267553204,-0.0429680349387,0.438909021868,-0.0549235929403,-0.00176280411289,0.0168842161271,-0.0245477451033,0.103534103547,0.190875334952,-0.0160077971357,-1.13916725717,-0.0578280272522,0.618283515386,0.0218745277242,-0.0637461100123,0.00666421528081,0.0276254007423,-0.042759151837,-0.0145850642315,-0.00880446485194,0.000126716038755,0.00433140420099,0.0308245755082,-0.00623921726713,-0.0318217746795,-0.0382440579868,0.000428347914493,0.000530399307534,-0.0759717737756,0.0354515033891,0.130639143673,-0.141494874567,0.0838856126349,-0.0194418010364,0.0137972983237,0.000531338760413,0.00134150184801,0.261957858812,0.0237711884021,0.0230326428759,0.0219937855594,0.00719528755352,0.0333485055281,0.00833840466389,-0.0250022671701,0.0732187999699,0.0409463350505,-0.00163879777058,0.0323944604152,0.0248038687327,0.00763331851835,-0.00540476791599,-0.0700331001035,0.636770876239,0.0270714128914,-0.0562305127792,0.0369742780132,-0.00482469423333,-0.153208622043,-0.169948249631,0.0822114655752,-0.000810202457017,0.0592939745916,0.0210041288368,0.0424686903816,0.013082261434,-0.0270151903807,0.0226204321573,0.00337807861336,0.0552972148331,0.00137329198924,0.00410977518032,-0.0788631223297,0.0195763268983,-0.011867418399,0.000136137516823,0.0489199529798,-0.0272194722771,0.0126117026801,-0.422521768213,0.0175167663074,-0.513577519799,-0.304908016713,-0.0153815043354,0.0143756230195,0.038892601783,0.00785100547614,0.024633644749,0.0565278241742,-0.019980734894,0.100938716186,0.0274989424604,0.0103429343526,-0.0533430239958,0.0319011843986,-0.0168859775771,-0.0443695710743,-0.0079129398118,-0.0125144644331,0.13605025411,-0.0162963376194,-0.000710295461299,0.0144422401202,-0.0184620116687,0.0804442274609,-0.0234468286624,-0.0238108738443,0.00860171509498,0.0081484941037,0.088244064232,-0.0116517274912,0.0175709303652,-0.0626241393835,-0.0854107365903,-0.0351575090354,0.0380456765128,0.0180095979816,-0.0209914241928,0.163106660981,0.127053320056,-0.0335430235607,-0.0109767864904,0.0709995225815,0.0167076809919,0.027726097262,-0.0311204836595,-0.0259199476295,0.180810035412,-0.0075547491507,-0.0081006110325,0.0270585413405,-0.0148313935713,0.0337146203424,0.0736048267004,-0.182810465676,-0.0267899729122,0.000179219280158,-0.0981396318556,0.0162153149149,0.0158205889243,0.0135732439379,-0.0122793913668,-0.0248816557428,-0.0839578376417,0.00599848509353,0.114707262204,-0.0328007287819,0.0467560652885,0.313179556657,0.024121214556,-0.0553332419857,-0.00684296908044,0.174685776575,0.00418298437096,0.015624947957,-0.0357577181683,-0.0335658241296,-0.0413500938049,0.00890996222676,-0.191520167295,-0.02223857119,-0.00900410728578,-0.00101642281143,-0.0751063838566,-0.00779308778792,-0.0339048097301,-0.29873321989,-0.00751397119331,0.0020689071961,-0.0334433996129,0.0798526578962,-0.00314060942661,0.000994142874497,-0.00385208084616,0.00639638012896,0.00432347948574,-0.0295723516279,-0.0282409806726,-0.243877258982,0.0306503469536,-0.0229985748532,0.0284501391965,-0.198174324275,-0.0179711916393,0.0143267555469,-0.0287066071347,0.000282523969584,0.0616495560776,-0.0172220711262,-0.0687083629936,-0.00370051948645,-0.0219797414557,0.15847905705,0.0354483161821,0.0763267553204,-0.0429680349387,0.438909021868,-0.0549235929403,-0.00176280411289,0.0168842161271,-0.0245477451033,0.103534103547,0.190875334952,-0.0160077971357,-1.13916725717,-0.0578280272522,0.618283515386,0.0218745277242,-0.0637461100123,0.00666421528081,0.0276254007423,-0.042759151837,-0.0145850642315,-0.00880446485194,0.000126716038755,0.00433140420099,0.0308245755082,-0.00623921726713,-0.0318217746795,-0.0382440579868,0.000428347914493,0.000530399307534,-0.0759717737756,0.0354515033891,0.130639143673,-0.141494874567,0.0838856126349,-0.0194418010364,0.0137972983237,0.000531338760413,0.00134150184801,0.261957858812,0.0237711884021,0.0230326428759,0.0219937855594,0.00719528755352,0.0333485055281,0.00833840466389,-0.0250022671701,0.0732187999699,0.0409463350505,-0.00163879777058,0.0323944604152,0.0248038687327,0.00763331851835,-0.00540476791599,-0.0700331001035,0.636770876239,0.0270714128914,-0.0562305127792,0.0369742780132,-0.00482469423333,-0.153208622043,-0.169948249631,0.0822114655752,-0.000810202457017,0.0592939745916,0.0210041288368,0.0424686903816,0.013082261434,-0.0270151903807,0.0226204321573,0.00337807861336,0.0552972148331,0.00137329198924,0.00410977518032,-0.0788631223297,0.0195763268983,-0.011867418399,0.000136137516823,0.0489199529798,-0.0272194722771,0.0126117026801,-0.422521768213,0.0175167663074,-0.513577519799,-0.304908016713,-0.0153815043354,0.0143756230195,0.038892601783,0.00785100547614,0.024633644749,0.0565278241742,-0.019980734894,0.100938716186,0.0274989424604,0.0103429343526,-0.0533430239958,0.0319011843986,-0.0168859775771,-0.0443695710743,-0.0079129398118,-0.0125144644331,0.13605025411,-0.0162963376194,-0.000710295461299,0.0144422401202,-0.0184620116687,0.0804442274609,-0.0234468286624,-0.0238108738443,0.00860171509498,0.0081484941037,0.088244064232,-0.0116517274912,0.0175709303652,-0.0626241393835,-0.0854107365903,-0.0351575090354,0.0380456765128,0.0180095979816,-0.0209914241928,0.163106660981,0.127053320056,-0.0335430235607,-0.0109767864904,0.0709995225815,0.0167076809919,0.027726097262,-0.0311204836595,-0.0259199476295,0.180810035412,-0.0075547491507,-0.0081006110325,0.0270585413405,-0.0148313935713,0.0337146203424,0.0736048267004,-0.182810465676,-0.0267899729122,0.000179219280158,-0.0981396318556,0.0162153149149,0.0158205889243,0.0135732439379,-0.0122793913668,-0.0248816557428,-0.0839578376417,0.00599848509353,0.114707262204,-0.0328007287819,0.0467560652885,0.313179556657,0.024121214556,-0.0553332419857,-0.00684296908044,0.174685776575,0.00418298437096,0.015624947957,-0.0357577181683,-0.0335658241296,-0.0413500938049,0.00890996222676,-0.191520167295,-0.02223857119,-0.00900410728578,-0.00101642281143,-0.0751063838566,-0.00779308778792,-0.0339048097301,-0.29873321989,-0.00751397119331,0.0020689071961,-0.0334433996129,0.0798526578962,-0.00314060942661,0.000994142874497,-0.00385208084616,0.00639638012896,0.00432347948574,-0.0295723516279,-0.0282409806726,-0.243877258982,0.0306503469536,-0.0229985748532,0.0284501391965,-0.198174324275,-0.0179711916393,0.0143267555469,-0.0287066071347,0.000282523969584,0.0616495560776,-0.0172220711262,-0.0687083629936,-0.00370051948645,-0.0219797414557,0.15847905705,0.0354483161821,0.0763267553204,-0.0429680349387,0.438909021868,-0.0549235929403,-0.00176280411289,0.0168842161271,-0.0245477451033,0.103534103547,0.190875334952,-0.0160077971357,-1.13916725717,-0.0578280272522,0.618283515386,0.0218745277242,-0.0637461100123,0.00666421528081,0.0276254007423,-0.042759151837,-0.0145850642315,-0.00880446485194,0.000126716038755,0.00433140420099,0.0308245755082,-0.00623921726713,-0.0318217746795,-0.0382440579868,0.000428347914493,0.000530399307534,-0.0759717737756,0.0354515033891,0.130639143673,-0.141494874567,0.0838856126349,-0.0194418010364,0.0137972983237,0.000531338760413,0.00134150184801,0.261957858812,0.0237711884021,0.0230326428759,0.0219937855594,0.00719528755352,0.0333485055281,0.00833840466389,-0.0250022671701,0.0732187999699,0.0409463350505,-0.00163879777058,0.0323944604152,0.0248038687327,0.00763331851835,-0.00540476791599,-0.0700331001035,0.636770876239,0.0270714128914,-0.0562305127792,0.0369742780132,-0.00482469423333,-0.153208622043,-0.169948249631,0.0822114655752,-0.000810202457017,0.0592939745916,0.0210041288368,0.0424686903816,0.013082261434,-0.0270151903807,0.0226204321573,0.00337807861336,0.0552972148331,0.00137329198924,0.00410977518032,-0.0788631223297,0.0195763268983,-0.011867418399,0.000136137516823,0.0489199529798,-0.0272194722771,0.0126117026801,-0.422521768213,0.0175167663074,-0.513577519799,-0.304908016713,-0.0153815043354,0.0143756230195,0.038892601783,0.00785100547614,0.024633644749,0.0565278241742,-0.019980734894,0.100938716186,0.0274989424604,0.0103429343526,-0.0533430239958,0.0319011843986,-0.0168859775771,-0.0443695710743,-0.0079129398118,-0.0125144644331,0.13605025411,-0.0162963376194,-0.000710295461299,0.0144422401202,-0.0184620116687,0.0804442274609,-0.0234468286624,-0.0238108738443,0.00860171509498,0.0081484941037,0.088244064232,-0.0116517274912,0.0175709303652,-0.0626241393835,-0.0854107365903,-0.0351575090354,0.0380456765128,0.0180095979816,-0.0209914241928,0.163106660981,0.127053320056,-0.0335430235607,-0.0109767864904,0.0709995225815,0.0167076809919,0.027726097262,-0.0311204836595,-0.0259199476295,0.180810035412,-0.0075547491507,-0.0081006110325,0.0270585413405,-0.0148313935713,0.0337146203424,0.0736048267004,-0.182810465676,-0.0267899729122,0.000179219280158,-0.0981396318556,0.0162153149149,0.0158205889243,0.0135732439379,-0.0122793913668,-0.0248816557428,-0.0839578376417,0.00599848509353,0.114707262204,-0.0328007287819,0.0467560652885,0.313179556657,0.024121214556,-0.0553332419857,-0.00684296908044,0.174685776575,0.00418298437096,0.015624947957,-0.0357577181683,-0.0335658241296,-0.0413500938049,0.00890996222676,-0.191520167295,-0.02223857119,-0.00900410728578,-0.00101642281143,-0.0751063838566,-0.00779308778792,-0.0339048097301,-0.29873321989,-0.00751397119331,0.0020689071961,-0.0334433996129,0.0798526578962,-0.00314060942661,0.000994142874497,-0.00385208084616,0.00639638012896,0.00432347948574,-0.0295723516279,-0.0282409806726,-0.243877258982,0.0306503469536,-0.0229985748532,0.0284501391965,-0.198174324275,-0.0179711916393,0.0143267555469,-0.0287066071347,0.000282523969584,0.0616495560776,-0.0172220711262,-0.0687083629936,-0.00370051948645,-0.0219797414557,0.15847905705,0.0354483161821,0.0763267553204,-0.0429680349387,0.438909021868,-0.0549235929403,-0.00176280411289,0.0168842161271,-0.0245477451033,0.103534103547,0.190875334952,-0.0160077971357,-1.13916725717,-0.0578280272522,0.618283515386,0.0218745277242,-0.0637461100123,0.00666421528081,0.0276254007423,-0.042759151837,-0.0145850642315,-0.00880446485194,0.000126716038755,0.00433140420099,0.0308245755082,-0.00623921726713,-0.0318217746795,-0.0382440579868,0.000428347914493,0.000530399307534,-0.0759717737756,0.0354515033891,0.130639143673,-0.141494874567,0.0838856126349,-0.0194418010364,0.0137972983237,0.000531338760413,0.00134150184801,0.261957858812,0.0237711884021,0.0230326428759,0.0219937855594,0.00719528755352,0.0333485055281,0.00833840466389,-0.0250022671701,0.0732187999699,0.0409463350505,-0.00163879777058,0.0323944604152,0.0248038687327,0.00763331851835,-0.00540476791599,-0.0700331001035,0.636770876239,0.0270714128914,-0.0562305127792,0.0369742780132,-0.00482469423333,-0.153208622043,-0.169948249631,0.0822114655752,-0.000810202457017,0.0592939745916,0.0210041288368,0.0424686903816,0.013082261434,-0.0270151903807,0.0226204321573,0.00337807861336,0.0552972148331,0.00137329198924,0.00410977518032,-0.0788631223297,0.0195763268983,-0.011867418399,0.000136137516823,0.0489199529798,-0.0272194722771,0.0126117026801,-0.422521768213,0.0175167663074,-0.513577519799,-0.304908016713,-0.0153815043354,0.0143756230195,0.038892601783,0.00785100547614,0.024633644749,0.0565278241742,-0.019980734894,0.100938716186,0.0274989424604,0.0103429343526,-0.0533430239958,0.0319011843986,-0.0168859775771,-0.0443695710743,-0.0079129398118,-0.0125144644331,0.13605025411,-0.0162963376194,-0.000710295461299,0.0144422401202,-0.0184620116687,0.0804442274609,-0.0234468286624,-0.0238108738443,0.00860171509498,0.0081484941037,0.088244064232,-0.0116517274912,0.0175709303652,-0.0626241393835,-0.0854107365903,-0.0351575090354,0.0380456765128,0.0180095979816,-0.0209914241928,0.163106660981,0.127053320056,-0.0335430235607,-0.0109767864904,0.0709995225815,0.0167076809919,0.027726097262,-0.0311204836595,-0.0259199476295,0.180810035412,-0.0075547491507,-0.0081006110325,0.0270585413405,-0.0148313935713,0.0337146203424,0.0736048267004,-0.182810465676,-0.0267899729122,0.000179219280158,-0.0981396318556,0.0162153149149,0.0158205889243,0.0135732439379,-0.0122793913668,-0.0248816557428,-0.0839578376417,0.00599848509353,0.114707262204,-0.0328007287819,0.0467560652885,0.313179556657,0.024121214556,-0.0553332419857,-0.00684296908044,0.174685776575,0.00418298437096,0.015624947957,-0.0357577181683,-0.0335658241296,-0.0413500938049,0.00890996222676,-0.191520167295,-0.02223857119,-0.00900410728578,-0.00101642281143,-0.0751063838566,-0.00779308778792,-0.0339048097301,-0.29873321989,-0.00751397119331,0.0020689071961,-0.0334433996129,0.0798526578962,-0.00314060942661,0.000994142874497,-0.00385208084616,0.00639638012896,0.00432347948574,-0.0295723516279,-0.0282409806726,-0.243877258982,0.0306503469536,-0.0229985748532,0.0284501391965,-0.198174324275,-0.0179711916393,0.0143267555469,-0.0287066071347,0.000282523969584,0.0616495560776,-0.0172220711262,-0.0687083629936,-0.00370051948645,-0.0219797414557,0.15847905705,0.0354483161821,0.0763267553204,-0.0429680349387,0.438909021868,-0.0549235929403,-0.00176280411289,0.0168842161271,-0.0245477451033,0.103534103547,0.190875334952,-0.0160077971357,-1.13916725717,-0.0578280272522,0.618283515386,0.0218745277242,-0.0637461100123,0.00666421528081,0.0276254007423,-0.042759151837,-0.0145850642315,-0.00880446485194,0.000126716038755,0.00433140420099,0.0308245755082,-0.00623921726713,-0.0318217746795,-0.0382440579868,0.000428347914493,0.000530399307534,-0.0759717737756,0.0354515033891,0.130639143673,-0.141494874567,0.0838856126349,-0.0194418010364,0.0137972983237,0.000531338760413,0.00134150184801,0.261957858812,0.0237711884021,0.0230326428759,0.0219937855594,0.00719528755352,0.0333485055281,0.00833840466389,-0.0250022671701,0.0732187999699,0.0409463350505,-0.00163879777058,0.0323944604152,0.0248038687327,0.00763331851835,-0.00540476791599,-0.0700331001035,0.636770876239,0.0270714128914,-0.0562305127792,0.0369742780132,-0.00482469423333,-0.153208622043,-0.169948249631,0.0822114655752,-0.000810202457017,0.0592939745916,0.0210041288368,0.0424686903816,0.013082261434,-0.0270151903807,0.0226204321573,0.00337807861336,0.0552972148331,0.00137329198924,0.00410977518032,-0.0788631223297,0.0195763268983,-0.011867418399,0.000136137516823,0.0489199529798,-0.0272194722771,0.0126117026801,-0.422521768213,0.0175167663074,-0.513577519799,-0.304908016713,-0.0153815043354,0.0143756230195,0.038892601783,0.00785100547614,0.024633644749,0.0565278241742,-0.019980734894,0.100938716186,0.0274989424604,0.0103429343526,-0.0533430239958,0.0319011843986,-0.0168859775771,-0.0443695710743,-0.0079129398118,-0.0125144644331,0.13605025411,-0.0162963376194,-0.000710295461299,0.0144422401202,-0.0184620116687,0.0804442274609,-0.0234468286624,-0.0238108738443,0.00860171509498,0.0081484941037,0.088244064232,-0.0116517274912,0.0175709303652,-0.0626241393835,-0.0854107365903,-0.0351575090354,0.0380456765128,0.0180095979816,-0.0209914241928,0.163106660981,0.127053320056,-0.0335430235607,-0.0109767864904,0.0709995225815,0.0167076809919,0.027726097262,-0.0311204836595,-0.0259199476295,0.180810035412,-0.0075547491507,-0.0081006110325,0.0270585413405,-0.0148313935713,0.0337146203424,0.0736048267004,-0.182810465676,-0.0267899729122,0.000179219280158,-0.0981396318556,0.0162153149149,0.0158205889243,0.0135732439379,-0.0122793913668,-0.0248816557428,-0.0839578376417,0.00599848509353,0.114707262204,-0.0328007287819,0.0467560652885,0.313179556657,0.024121214556,-0.0553332419857,-0.00684296908044,0.174685776575,0.00418298437096,0.015624947957,-0.0357577181683,-0.0335658241296,-0.0413500938049,0.00890996222676,-0.191520167295,-0.02223857119,-0.00900410728578,-0.00101642281143,-0.0751063838566,-0.00779308778792,-0.0339048097301,-0.29873321989,-0.00751397119331,0.0020689071961,-0.0334433996129,0.0798526578962,-0.00314060942661,0.000994142874497,-0.00385208084616,0.00639638012896,0.00432347948574,-0.0295723516279,-0.0282409806726,-0.243877258982,0.0306503469536,-0.0229985748532,0.0284501391965,-0.198174324275,-0.0179711916393,0.0143267555469,-0.0287066071347,0.000282523969584,0.0616495560776,-0.0172220711262,-0.0687083629936,-0.00370051948645,-0.0219797414557,0.15847905705,0.0354483161821,0.0763267553204,-0.0429680349387,0.438909021868,-0.0549235929403,-0.00176280411289,0.0168842161271,-0.0245477451033,0.103534103547,0.190875334952,-0.0160077971357,-1.13916725717,-0.0578280272522,0.618283515386,0.0218745277242,-0.0637461100123,0.00666421528081,0.0276254007423,-0.042759151837,-0.0145850642315,-0.00880446485194,0.000126716038755,0.00433140420099,0.0308245755082,-0.00623921726713,-0.0318217746795,-0.0382440579868,0.000428347914493,0.000530399307534,-0.0759717737756,0.0354515033891,0.130639143673,-0.141494874567,0.0838856126349,-0.0194418010364,0.0137972983237,0.000531338760413,0.00134150184801,0.261957858812,0.0237711884021,0.0230326428759,0.0219937855594,0.00719528755352,0.0333485055281,0.00833840466389,-0.0250022671701,0.0732187999699,0.0409463350505,-0.00163879777058,0.0323944604152,0.0248038687327,0.00763331851835,-0.00540476791599,-0.0700331001035,0.636770876239,0.0270714128914,-0.0562305127792,0.0369742780132,-0.00482469423333,-0.153208622043,-0.169948249631,0.0822114655752,-0.000810202457017,0.0592939745916,0.0210041288368,0.0424686903816,0.013082261434,-0.0270151903807,0.0226204321573,0.00337807861336,0.0552972148331,0.00137329198924,0.00410977518032,-0.0788631223297,0.0195763268983,-0.011867418399,0.000136137516823,0.0489199529798,-0.0272194722771,0.0126117026801,-0.422521768213,0.0175167663074,-0.513577519799,-0.304908016713,-0.0153815043354,0.0143756230195,0.038892601783,0.00785100547614,0.024633644749,0.0565278241742,-0.019980734894,0.100938716186,0.0274989424604,0.0103429343526,-0.0533430239958,0.0319011843986,-0.0168859775771,-0.0443695710743,-0.0079129398118,-0.0125144644331,0.13605025411,-0.0162963376194,-0.000710295461299,0.0144422401202,-0.0184620116687,0.0804442274609,-0.0234468286624,-0.0238108738443,0.00860171509498]
7: sum = 0.0
8: for i in range(len(vec)):
9: sum += vec[i] * vec[i]
10: return sum
11:
12: if __name__ == "__main__":
13: start = time.clock()
14:
15: for i in range(100000):
16: dot()
17:
18: print '\n dot product = ',dot(),'\n'
19:
20: end = time.clock()
21: print end - start, 'seconds.'
注释掉psyco.full()这句话后执行时间为：26.48s，去掉注释后执行时间为：4.6s，改成C代码执行时间为：0.58s，一般情况下psyco都会加快运行速度，当然和C相比其实还是差距明显的，相关链接如下：
1)、可爱的 Python: 用 Psyco 让 Python 运行得像 C 一样快》：http://www.ibm.com/developerworks/cn/linux/sdk/python/charm-28/
2)、psyco主页：http://psyco.sourceforge.net/download.html，在ubuntu下可以这么安装：sudo apt-get install python-psyco
7、关于分类器的评价采用如下指标：
1)、
2)、
3)、
4)、
5)、
6)、
7)、、
8、运行环境：
OS：32bits ubuntu 10.04
CPU：Intel(R) Pentium(R) Dual CPU E2200 @ 2.20GHz
memory：DIMM DDR2 Synchronous 667 MHz (1.5 ns) 2G
IDE：Eclipse + Pydev
9、程序中用到的数据集主要来自UCI Data Set和Libsvm Data：
1)、pymining data：data/train.txt和data/test.txt
DATA ------- 0 ex. ------- 1 ex. -------- 2 ex. ---------- 3 ex. ------------ TotalTraining set 149 --------- 36 --------- 102 ---------- 63 ------------ 350
Validation set 85 --------- 14 --------- 35 ---------- 16 ------------ 150
Number of features：卡方检验过滤后
Total：1862
C = 100,kernel = RBF,gamma = 0.03,npRatio=1,测试结果如下：
(1)、类别0标记为1，其它标记为-1，
Recall = 0.929411764706 Precision = 0.840425531915 Accuracy = 0.86
F(beta=1) = 0.564005241516 F(beta=2) = 0.676883364786 AUCb = 0.849321266968
(2)、类别1标记为1，其它标记为-1，
Recall = 0.929411764706 Precision = 0.840425531915 Accuracy = 0.86
F(beta=1) = 0.564005241516 F(beta=2) = 0.676883364786 AUCb = 0.849321266968
(3)、类别2标记为1，其它标记为-1，
Recall = 0.6 Precision = 0.913043478261 Accuracy = 0.893333333333
F(beta=1) = 0.43598615917 F(beta=2) = 0.496845425868 AUCb = 0.791304347826
(4)、类别3标记为1，其它标记为-1，
Recall = 0.25 Precision = 1.0 Accuracy = 0.92
F(beta=1) = 0.222222222222 F(beta=2) = 0.238095238095 AUCb = 0.625
2)、Arcene：http://archive.ics.uci.edu/ml/datasets/Arcene
ARCENE -- Positive ex. -- Negative ex. – Total
Training set 44 ----------- 56 --------- 100
Validation set 44 ----------- 56 --------- 100
Number of variables/features/attributes：
Real: 7000
Probes: 3000
Total: 10000
C = 100,kernel = RBF,gamma = 0.000000001,npRatio=1,测试结果如下：
Recall = 0.772727272727 Precision = 0.85 Accuracy = 0.84
F(beta=1) = 0.500866551127 F(beta=2) = 0.584074373484 AUCb = 0.832792207792
3)、SPECT Heart Data Set ：http://archive.ics.uci.edu/ml/datasets/SPECT+Heart
SPECT ------ Positive ex. -- Negative ex. – Total
Training set 40------------ 40---------- 80
Validation set 172 ---------- 15--------- 187
Attribute Information:
OVERALL_DIAGNOSIS: 0,1 (class attribute, binary)
F1: 0,1 (the partial diagnosis 1, binary)
F2: 0,1 (the partial diagnosis 2, binary)
F3: 0,1 (the partial diagnosis 3, binary)
F4: 0,1 (the partial diagnosis 4, binary)
F5: 0,1 (the partial diagnosis 5, binary)
F6: 0,1 (the partial diagnosis 6, binary)
F7: 0,1 (the partial diagnosis 7, binary)
F8: 0,1 (the partial diagnosis 8, binary)
F9: 0,1 (the partial diagnosis 9, binary)
F10: 0,1 (the partial diagnosis 10, binary)
F11: 0,1 (the partial diagnosis 11, binary)
F12: 0,1 (the partial diagnosis 12, binary)
F13: 0,1 (the partial diagnosis 13, binary)
F14: 0,1 (the partial diagnosis 14, binary)
F15: 0,1 (the partial diagnosis 15, binary)
F16: 0,1 (the partial diagnosis 16, binary)
F17: 0,1 (the partial diagnosis 17, binary)
F18: 0,1 (the partial diagnosis 18, binary)
F19: 0,1 (the partial diagnosis 19, binary)
F20: 0,1 (the partial diagnosis 20, binary)
F21: 0,1 (the partial diagnosis 21, binary)
F22: 0,1 (the partial diagnosis 22, binary)
C = 100,kernel = RBF,gamma = 15,npRatio=1,测试结果如下：
Recall = 0.93023255814 Precision = 0.958083832335 Accuracy = 0.898395721925
F(beta=1) = 0.617135142954 F(beta=2) = 0.756787437329 AUCb = 0.731782945736
4)、Dexter：http://archive.ics.uci.edu/ml/datasets/Dexter
DEXTER -- Positive ex. -- Negative ex. – Total
Training set 150 ---------- 150 -------- 300
Validation set 150 ---------- 150 -------- 300
Test set 1000 --------- 1000 ------- 2000 (缺少label)
Number of variables/features/attributes:
Real: 9947
Probes: 10053
Total: 20000
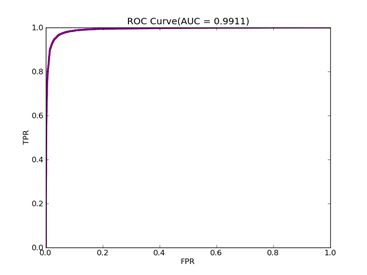
C = 100,kernel = RBF, gamma = 0.000001,npRatio=1,测试结果如下：
Recall = 0.986666666667 Precision = 0.822222222222 Accuracy = 0.886666666667
F(beta=1) = 0.577637130802 F(beta=2) = 0.698291252232 AUCb = 0.886666666667
5)、Mushrooms：原始数据集在：http://archive.ics.uci.edu/ml/datasets/Mushroom
预处理以后的在：http://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/binary/mushrooms
MUSHROOMS-- Positive ex.（lbael=1） -- Negative ex.（lbael=2） – Total
Data set 3916 ----------------------- 4208 ------------------- 8124
C = 100,kernel = RBF,gamma = 0.00001,npRatio=1,测试结果如下：
Recall = 1.0 Precision = 0.942615239887 Accuracy = 0.960897435897
F(beta=1) = 0.640664961637 F(beta=2) = 0.793097989552 AUCb = 0.945340501792
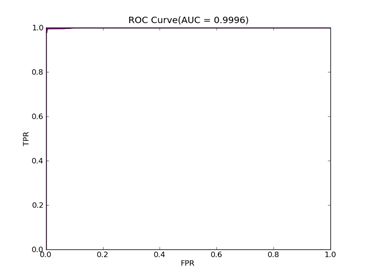6)、 Adult：原始数据集在：http://archive.ics.uci.edu/ml/datasets/Adult
预处理以后的在：http://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/binary.html a1a
ADULT ------ Positive ex.（lbael=+1） --- Negative ex.（lbael=-1） – Total
Training set 395 -------------------- 1210 ----------------- 1605
Validation set 7446 -------------------- 23510 ----------------- 30956
Number of variables/features/attributes: 123 C = 100,kernel = RBF,gamma = 0.08,npRatio=1,测试结果如下：
Recall = 0.598710717164 Precision = 0.588281868567 Accuracy = 0.802687685748
F(beta=1) = 0.322095887953 F(beta=2) = 0.339513363093 AUCb = 0.733000615919
由于正例少于负例,调整模型的npRatio=10,测试结果如下：
Recall = 0.620198764437 Precision = 0.602243088159 Accuracy = 0.810117586251
F(beta=1) = 0.336126156669 F(beta=2) = 0.357601319181 AUCb = 0.745233367757
其它参数不变，npRatio=100,测试结果如下：
Recall = 0.6952726296 Precision = 0.595399654974 Accuracy = 0.813057242538
F(beta=1) = 0.361435449815 F(beta=2) = 0.39122162696 AUCb = 0.772817088939
可以从上面的实验看到处理不平衡数据时候，对正例和负例赋予不同的C值方法的作用。
7）、Fourclass： 数据集在：http://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/binary/fourclass
FOURCLASS-- Positive ex.（lbael=1） -- Negative ex.（lbael=2） – Total
Fourclass set 307 ----------------------- 557 ------------------- 864
C = 100,kernel = RBF,gamma = 0.01,npRatio=1,测试结果如下：
Recall = 0.991071428571 Precision = 1.0 Accuracy = 0.996415770609
F(beta=1) = 0.662686567164 F(beta=2) = 0.827123695976 AUCb = 0.995535714286
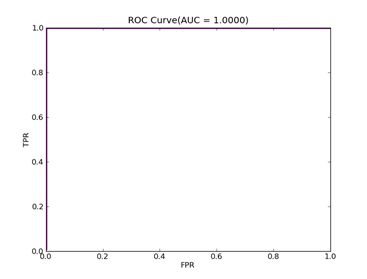8）、Splice：http://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/binary.html splice
SPLICE-- Positive ex.（lbael=1） -- Negative ex.（lbael=2） – Total
Training set 517 --------------------- 483 --------------- 1000
Validation set 1131 -------------------- 1044 -------------- 2175
Number of variables/features/attributes: 60 C = 100,kernel = RBF,gamma = 0.01,npRatio=1,测试结果如下：
Recall = 0.885057471264 Precision = 0.912488605287 Accuracy = 0.896091954023
F(beta=1) = 0.577366617352 F(beta=2) = 0.696505768897 AUCb = 0.896551724138
9)、RCV1.BINARY：http://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/binary.html
RCV1.BINARY------Total
Training set 20242
Validation set 677399
Number of features:
Total: 47236
Recall = 0.956610366919 Precision = 0.964097045588 Accuracy = 0.9593
F(beta=1) = 0.631535514017 F(beta=2) = 0.778847158177 AUCb = 0.959383756361
10)、Madelon：http://archive.ics.uci.edu/ml/datasets/Madelon
MADELON -- Positive ex. -- Negative ex. – Total
Training set 1000 --------- 1000 ------- 2000
Validation set 300 ---------- 300 -------- 600
Test set 900 ---------- 900 -------- 1800
Number of variables/features/attributes:
Real: 20
Probes: 480
Total: 500
Recall = 0.673333333333 Precision = 0.724014336918 Accuracy = 0.708333333333
F(beta=1) = 0.406701950583 F(beta=2) = 0.451613474471 AUCb = 0.708333333333
11)、GISETTE：http://archive.ics.uci.edu/ml/datasets/Gisette
GISETTE -- Positive ex. -- Negative ex. – Total
Training set 3000 -------- 3000 ------- 6000
Validation set 500 --------- 500 ---------1000
Test set 3250 -------- 3250 ------- 6500
Number of variables/features/attributes:
Real: 2500
Probes: 2500
Total: 5000
Recall = 0.972 Precision = 0.983805668016 Accuracy = 0.978
F(beta=1) = 0.647037875094 F(beta=2) = 0.802795761493 AUCb = 0.978
12)、Australian：http://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/binary.html
GISETTE -- Positive ex. -- Negative ex. – Total
Training set 201 --------- 251 -------- 452
Validation set 106 --------- 132 ---------238
Number of features:
Total: 14
Recall = 0.801886792453 Precision = 0.643939393939 Accuracy = 0.714285714286
F(beta=1) = 0.422243001578 F(beta=2) = 0.474093808236 AUCb = 0.722913093196
13)、Svmguide1：http://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/binary.html
GISETTE -- Positive ex. -- Negative ex. – Total
Training set 2000 --------- 1089 -------- 3089
Validation set 2000 --------- 2000 ---------4000
Number of features:
Total: 4
Recall = 0.964 Precision = 0.957774465971 Accuracy = 0.96075
F(beta=1) = 0.632009483243 F(beta=2) = 0.7795759451 AUCb = 0.96075
5、并行点
如果期望在并行计算框架中运行SMO，我可以想到的并行点如下：
1)、选择最大违反对时，可以先在每台机器上找到局部MVP，最后由master选择全局MVP；
2)、更新一阶导数数组，各个机器更新自己本地部分就可以了；
3)、对sparse matrix向量求内积，可以用map函数映射为key/value对，其中key为column标号，value为对应的取值，reduce函数根据key计算乘积并累加。
想要使两个拉格朗日乘子的优化过程实现并行似乎很有难度，目前没有想到好方法。
6、总结
本文介绍了如何通过优化拉格朗日乘子的选择来提高SMO算法性能的方法，SMO算法的核心思想是每次选择两个拉格朗日乘子进行优化，因此其主要矛盾就落在了优先优化哪些乘子身上，目前对乘子选择最好的方法之一是利用对偶问题的KKT条件来寻找最大违反对(MVP)，而寻找MVP的方法又可以利用一阶信息和二阶信息，其中又以后者效果较好，它对MVP的选定不仅考虑它们之间值的差距，而且考虑两个乘子之间的伪距离。
如果数据分布不平衡，训练出的分类器精度等常规指标可能很高，但是实际应用时就会出现问题，典型的例子是漏油检测，处理这类问题可以从三个方面入手：预处理数据集本身、使用不同惩罚系数、使用特殊核函数，它们各有优缺点，没有最好只有最合适，本文采用第二种方法，实现起来也比较容易，评价指标采用ROC Curve、AUC，本文绘制ROC的方法采用Libsvm中的方法。
参数选择直接影响到分类器的性能，涉及的主要参数有：惩罚系数C，这个值越大代表越不想放弃离群点；npRatio，如果数据分布很不平衡，可以用它来调节惩罚系数，负例远大于正例时，npRatio>1，负例的C值要小于正例的C值，反之亦然；核函数参数，依据具体核函数确定。本文没有给出选择最优参数的方法。
7、参考文献
1)、《Improvements to Platt’s SMO Algorithm for SVM Classifier Design》
2)、《A Study on SMO-type Decomposition Methods for Support Vector Machines》
3)、《The Analysis of Decomposition Methods for Support Vector Machines》
4)、《Working Set Selection Using Second Order Information for Training Support Vector Machines》
5)、《Making Large-Scale SVM Learning Practical》
6)、《Optimizing Area Under Roc Curve with SVMs》
7)、《Applying Support Vector Machines to Imbalanced Datasets》
8)、《SVMs Modeling for Highly Imbalanced》