连通图总结及例题
【什么是连通图】
在图论中,连通图基于连通的概念。在一个无向图 G 中,若从顶点i到顶点j有路径相连(当然从j到i也一定有路径),则称i和j是连通的。如果 G 是有向图,那么连接i和j的路径中所有的边都必须同向。如果图中任意两点都是连通的,那么图被称作连通图。如果此图是有向图,则称为强连通图(注意:需要双向都有路径)。
连通图的题目有许多,我们先要了解:
文章的最下面有相关的例题,可以拿来练练手。
1.如何缩点,有向图和无向图的区别。
2.如何求割点,
3.如何求桥。
还有其他的没有学到,学到了再补~~
【缩点】
缩点就是要将两两之间可以相互到达的点,缩成一个点来表示(即求无向图的连通分量,或者有向图的强连通分量),他们的求法都是相同的,都是将无向图转化为有向图。
接下来我们讲一个算法,基本上都是以Trajan算法写题的。
【Trajan算法】
我们要引入两个数组,low数组,记录一个连通分量中的最小值(在这里说明一下,一个连通分量的low值不一定相等,在下面再讲解),DFN数组,记录的是第几个遍历到这个没有被访问过的点的(可能不是太懂,没关系,继续看)。
先给大家举个例子,例如:
4个点,4条边,如图所示
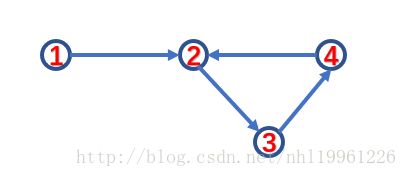
以有向图为例。
如果我们要缩点,肯定是将点2,3,4缩成一个点,因为他们两两之间能相互到达(如果是无向图,这里的两条路是不能相同的,例如:1-2,2-1,这是同一条路)。
下面我们看代码:
void Trajan(int u)//递归,深搜
{
lowpow[u]=DFN[u]=++dfs_clock;//将访问的点,low数组和pre赋值,
s.push(u);//将这个数压入栈中
for(int i=firs[u]; i!=-1; i=edge[i].nex)
{
int v=edge[i].v;
if(!DFN[v])//如果v没有被访问过
{
Trajan(v);//深搜,向下访问
//直到访问到头,递归回来后,
lowpow[u]=min(lowpow[u],lowpow[v]);//更新low数组的值,
}
else if(!sccnow[v])//如果v点被访问过,但没有被染色,就更新low的值
lowpow[u]=min(lowpow[u],DFN[v]);
}
//如果都与u相连的边都被访问过了,就开始染色,将是同一个连通分量的点,染成同一个点。
if(lowpow[u]==DFN[u])//如果low值和DFN的值,相等代表u是这个连通分量的开始的点(看不懂可以向下看)
{
scc_clock++;//这个是记录,有多少个连通分量了
while(1)
{
int x=s.top();
s.pop();
sccnow[x]=scc_clock;//sccnow记录x点被染成了那个数字,
sccinq[scc_clock]++;//记录这个数字的个数,即这个连通分量中点的个数
if(u==x) break;//如果全部染完,就结束了
}
}
}根据上面的例子,我们是这样遍历的:
for(int i=1; i<=n; i++)
if(!pre[i])
Trajan(i);(1)所以是从1开始的,先把1的low[1]=DFN[1]=1;然后放入栈中,
遍历与1相关连的边,先找到2,发现2没有被访问过,就搜索2.
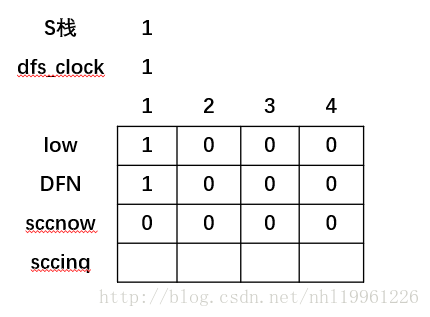
(2)再从2开始,把2的low[2]=DFN[2]=2;然后放入栈中,
遍历与2相关连的边,先找到3,发现3没有被访问过,就搜索3.
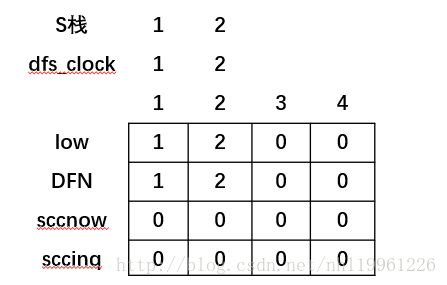
(3)再从3开始,把3的low[3]=DFN[3]=3;然后放入栈中,
遍历与3相关连的边,先找到4,发现4没有被访问过,就搜索4.
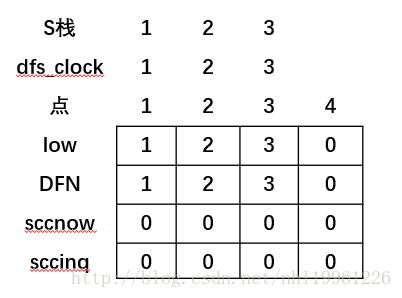
(4)再从4开始,把4的low[4]=DFN[4]=4;然后放入栈中,
遍历与4相关连的边,发现2,但是2被访问过了,就把4的lowpow[4]=min(lowpow[4],DFN[2]);更新。发现这时,lowpow[4]!=DFN[4],不执行里面的内容,返回到第三步。
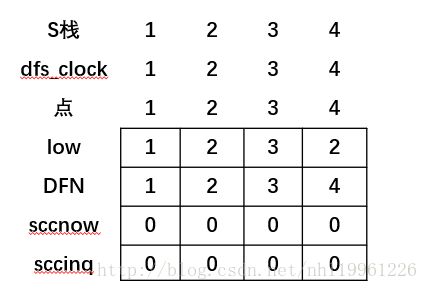
(5)接着返回到第三步,更新lowpow[3]=min(lowpow[3],lowpow[4]);,没有了点,跳出for循环,lowpow[3]!=DFN[3],不执行里面的内容,返回到第二步。
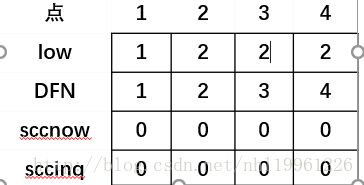
(6)接着返回到第二步,更新lowpow[2]=min(lowpow[2],lowpow[2]);,没有了点,跳出for循环。因为lowpow[2]==DFN[2],所以执行里面的内容,开始染色,
将栈头到点2的所有点都赋为点1,然后记录个数,返回第一步。
注意:这时候你会发现,栈里只剩下1了,而且2,3,4被染成了点1。
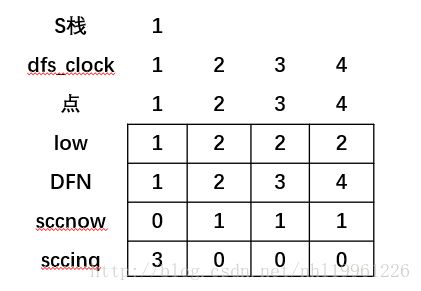
(7)接着返回到第一步,更新lowpow[1]=min(lowpow[1],lowpow[2]);,没有了点,跳出for循环。因为lowpow[1]==DFN[1],所以执行里面的内容,开始染色。
注意:这时候栈为空了,所有的点都被重新染色了,
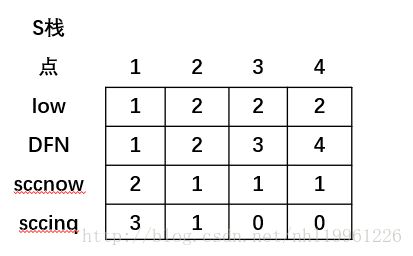
(9)程序结束。
这就是Trajan算法的全部过程了,并且包括染色,其他的问题都是用的这种方法,所以一定要弄过程,否则很容易混乱~~,如果还有不会的概念可以,留言或者百度。
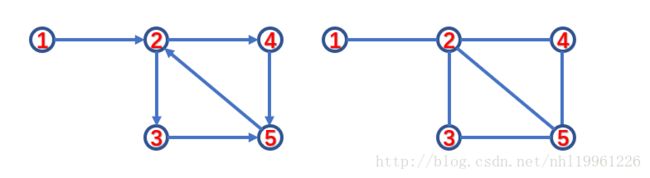
现在就说一说为什么,有向图和无向图的low值,在相同的连通分量中会不相同。
给你个样例自己试试:
如果这两幅图,他们的low值就不一样,可以动手试一试~~
【求割点】
割点一般是无向图的题目(有向图我也没有见过)。
割点的定义:将这个点去掉,图就会被分成两个部分(或者以上),那么这个点就是一个割点。
例如上面的右面的图,2是一个割点,1,3,4,5不是割点。
求割点的函数就是在Trajan算法的基础上,再加一些判断得来的。
首先要知道那些点是割点:
1、对根节点u,若其有两棵或两棵以上的子树,则该根结点u为割点;
2、对非叶子节点u(非根节点),若其子树的节点均没有指向u的祖先节点的回边,说明删除u之后,根结点与u的子树的节点不再连通;则节点u为割点。
这一点想一想还是能够理解的,实在不懂的可以找个图试一下,很简单的。
下面是求割点的算法,可以看一下,与上面缩点的算法是一样的,只不过加了一些判断割点的条件,而且缺少了染色的过程,那是因为无向图中同一个连通图的low值是一样的,这样就不需要染色了,而且这里本身好像也不需要染色。
void Trajan(int u,int pre)//u代表当前节点,pre代表u的父亲节点
{
low[u]=DFN[u]=++dfs_clock;
int sum=0;
for(int i=0; i//g是vector数组,没有学过的可以稍微看一下,很简单的
{
int v=g[u][i];//与u相连的点v
if(v==pre) continue;//如果v是u的父亲节点,代表它走了回路,因为这是无向图,要从新再找点
if(!DFN[v])//没有被标记过
{
Trajan(v,u);
low[u]=min(low[u],low[v]);
if(low[v]>=DFN[u])
{
sum++;//记录该点把图分成了几个部分,例如图:1——2——3,2把图分成了两个部分
if(u!=pre)//(1)割点不是根节点
cut[u]=1;
//(2)割点是根节点,并且将图分成的部分大于1,
//例如:1——2——3,1不是割点,因为他没有将图分开,sum没有大于1
if(u==pre&&sum>1)
cut[u]=1;
}
}
else low[u]=min(low[u],DFN[v]);
}
} 【求桥】
什么是桥:在一个无向图中,如果去掉一条边,使得图被分成了几个部分,那么这条边就被称为桥;
例如图:
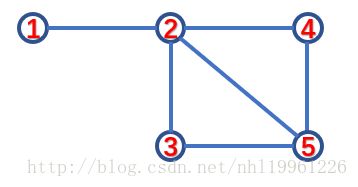
1——2这条边是桥,其余的边都不是桥,这与割点是不同的,割点看的是点,桥看的是边。
桥的判断条件只有一个:
当且仅当:low[v]>DFN[u],此时是桥
下面是代码:
void Trajan(int u,int pre)
{
low[u]=DFN[u]=++dfs_clock;
for(int i=firs[u]; i!=-1; i=edge[i].nex)
{
int v=edge[i].v;
if(v==pre) continue;
if(!DFN[v])
{
Trajan(v,u);
low[u]=min(low[u],low[v]);
if(low[v]>DFN[u])//判断是否为桥的条件
{
bridge_clock++;
edge[i].cut=edge[i^1].cut=1;//将这条边记录一下
}
}
else low[u]=min(low[u],DFN[v]);
}
}【下面是例题】
缩点:
- 题目链接:Network of Schools
- 题目链接:Redundant Paths
- 题目链接:迷宫城堡
割点:
- 题目链接:Network
桥:
- 题目链接:Critical Links
- 题目链接:SPF
- 题目链接:Caocao’s Bridges
- 题目链接:Burning Bridges
注:如有错误,请留言~~