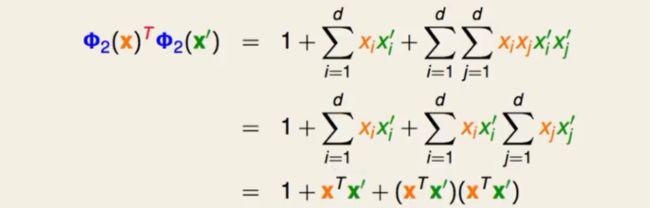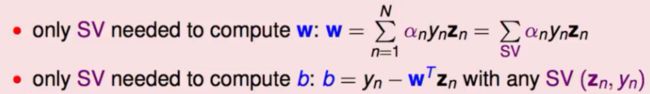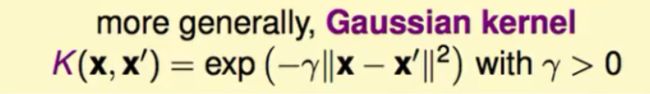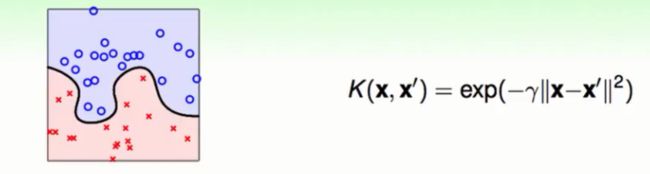机器学习之核函数支持向量机(机器学习技法)
为什么要有个核函数
在对偶支持向量机中我们谈到要避开特征转换后高VC维度空间给我们带来的计算复杂度的影响。但是单单的对偶问题没有实现这一点,对偶问题只是让计算看起来避开了VC维度带来的影响,但是这个VC维度还是潜藏在了计算的过程中。
上图是SVM的拉格朗日对偶问题转换为标准的二次规划问题(以下称之为QP问题)的结果。其中QD矩阵的计算中包含了Z向量的内积。而Z向量是由原始X空间(它的VC维度为d)经过特征转换后得到的新向量(Z的VC维度为d’)。在高维度的转化情况下d'远大于d,有时候碰上无限多维的转换,d'的值将会有无限大这时QD矩阵中的两笔资料的Z矩阵的内积的计算将十分困难。这时我们就需要核函数来帮忙了。
一个简单的案例
核函数(kernel function)的引出
现在我们就以一种全新的方法去计算QD矩阵中的Z矩阵的内积,我们的原始空间的维度是d,我们的转换是2次转换。如下图:
在以前的计算过程中我们要先将X空间的d维向量转换成Z空间中的d'维度的向量,d'远大于d。这时计算内积的时间复杂度是O(d')。
一种全新的思路是,我们不再使用中间变量Z向量而直接依靠原始空间(X空间)的资料的线性组合来完成。两个资料点的内积如下图:
X空间资料转换之后是一个二次多项式,我们分别将一次项与二次项分别对应做内积,然后将二次项的内积做一个等价变换得到上图所示的结果。整个过程简化为了两个资料点只在X空间做内积然后再用这个整体来计算转换后的内积,它的计算复杂度为O(d)远远小于O(d')(在d'远大于d的情况下)。如果我们想在d'为无限大的情况下我们就不可能完成这个转换而使用核函数可以轻松搞定,这一次我又被算法的强大所征服!
核函数的几个应用
在学习过核函数之后我们极大地简化了高维度给我们带来的计算上的复杂度。以此类推我们可以将SVM中其它用到特征转换后做内积的部分替换成核函数的方法。
b的计算与最后的SVM模型的计算都可以被简化:
从此我们的计算过程就不会受到d'的影响了。
小节
改版后的SVM的求法如下:
①计算出二次规划所需要的各个参数,尤其是使用核函数计算出Q矩阵。
②使用QP的软件计算出α的值。
③使用α计算出W与b(需要用到支撑向量)的值,b的计算涉及到两个资料点进行特征转换再做内积的步骤,统统都换成核函数的形式。
④返回最终求解的SVM。
其中有以下几个说明:
①计算Q矩阵的时间复杂度为O(N²)*核函数步骤的复杂度。
②QP问题中只有N个变数与N+1个约束条件,与转换后的VC维度无关。
③在上述的③④步骤中我们付出的复杂度是O(支持向量的个数)*核函数步骤的复杂度(因为在原始函数中想要计算W的内积就是需要用到支撑向量)。
核函数的进一步推广
最常用的2次转换核函数
在实务上我们通常会使用一个形式更为简单的二次核函数来解决问题,他是由原来的核函数经过放缩得到的如下:
上图中的绿色的Φ2就是一般用到的核函数放缩,我们直接称之为K2。与原来的蓝色Φ2相比它们拥有同样的复杂性(因为无论如何它们模型的维度是一样的只是模型的初始权重不同而已),模型的初始权重不同就会有不同的内积,不同的内积就会有不同的距离。而SVM是一个距离相关的演算法,距离不同体现在几何意义上就是模型的边界不同(我们在刚开始做线性的SVM的时候就是通过最小化W的内积来计算最大边界的:-)。由于K2比较简单所以它就是我们最常用的二次转换的核函数。
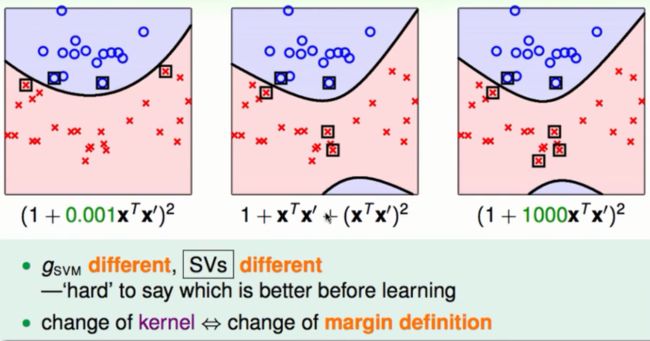
不同的核函数
实务上,面对相同的原始空间相同的资料与不同的核函数会得到不同的复杂度的模型与不同的支持向量。我们需要对核函数进行选择就像我们以前对不同的特征转换做选择一样。从原理上来看我们的核函数中包含了特征转换。
一般的多项式核函数
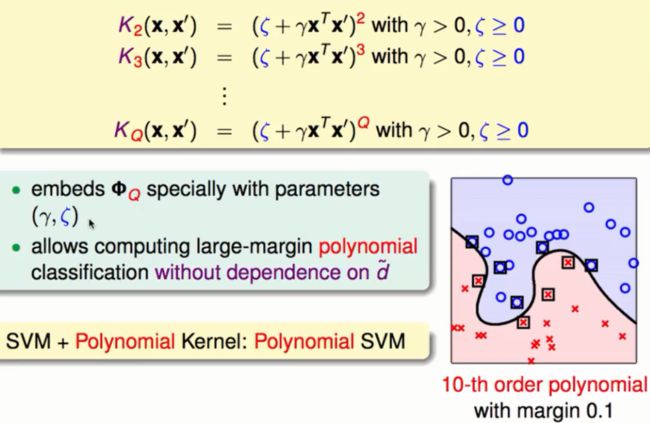
我们的核函数不仅可以是2次转换我们还可以推广到任意次的转换:
在一般化的过程中我们不仅将转换的次数推广到Q次,也将常数项进行了推广。在以后的计算中我们的计算复杂度只是原始空间里向量的内积再加上Q次方的运算步骤。
除了运算复杂度的减小,即使在高次的转换中我们也会有外边距的保证这样会使得我们的模型不容易过拟合。就像上面介绍的使用多项式核函数的SVM我们称之为多项式SVM。
一个特殊的转换:线性核函数
在所有转换都不做的情况下就诞生了线性的核函数,它是最基本的线性模型无需将原始问题转换为对偶问题来解决。在实务上也是我们首先测试的模型。
核函数的无限多维转换
高斯核函数假设我们现在的核函数是一个高斯函数(正态分布函数如上图),我们将一维的资料点带入。我们在进行一些泰勒展开之后会得到某一个形式式子的无限多的连加。根据展开式的特点,我们从中倒推出了这个特征转换的函数也就是图中的Φ(x)。Φ(x)是一个无限多维的式子,它对应了一个无限多维的特征转换,它隐藏在了一个高斯函数的核函数中。在此刻我们能够解决无限多维的特征转换了,我不得不佩服这些数学家,太强大了!
我们将这个高斯核函数进行推广得到:
在这里我们将一维的x推广到任意维度的X向量,与此同时我们又加上了γ作为系数来放缩。
高斯SVM的模型
我们使用高斯函数作为我们的核函数进行构造SVM会得到上图,SVM的计算只用到了所有资料点中的支持向量的部分。我们可以通过计算每个支持向量的高斯核函数的值进而计算b与W的值。总的来说,高斯SVM的模型是每一个支持向量上的高斯函数的线性组合,所以高斯的核函数通常也被称为RBF核函数(高斯的,线性组合的函数)。
使用这个模型我们可以实现无限多维的转换。
小节
在支撑向量机中我们既能够保证较小的模型集合的数量又能拥有复杂的边界。
在转换上面:我们不在执着于求出转换后的高维度资料Z,而是直接使用核函数去绕过这个步骤。
在计算上面:我们只需要用到我们的支撑向量。
在对付过拟合上面:我们有LargeMargin。
在转换上面:我们有高斯核,可以转换到无限多维空间。
需要注意的是:即使我们有了LargeMargin,在碰到高维的转换时(比如说高斯核)任然可能出现过拟合所以我们时刻要谨慎选择特征转换与其对应的参数。比如在高斯核中我们一般不推荐使用较大的γ。
核函数的选择(几个核函数的利弊)
线性核函数
优点:
①不容易过拟合,比较安全使我们的首选。
②比较简单可以不用对偶问题就能解决。
③我们可以清晰的看到模型与资料的长相来帮助我们做决策。
缺点:
不能够分割非线性的资料。
多项式核函数
优点:
①笔线性的模型更加灵活。
②我们可以根据自己对模型的理解进而去调节Q的大小。
缺点:
①涉及到的参数太多。
②Q比较大的时候计算比较困难。
建议:我们通常只使用小的Q,当转换空间后模型的维度不大的时候我们可以使用SVM原始的解法而无需使用对偶问题。
高斯核函数
优点:
①比线性模型和多项式模型更为复杂。
②参数较少容易调试。
③在数值上的计算困难度比多项式低一些。
缺点:
①我们并不能明确的说出每个权重的实际含义。
②需要一些等价问题的转换,解决速度上来说比较慢。
③太过于强大容易过拟合。
建议:最常使用但是又非常谨慎。
核函数的合法性
核函数代表一种相似性,在转换到高维空间后Z向量内积(内积就表示两个向量的相似性)的相似性。也就是说,不是任何的相似性都能够以核函数的方式表达出来。
判断一个核函数的两个条件就是:
①核函数是对称的,因为向量内积是对称的。
②将核函数中的资料点带入一个矩阵中如上图,得到的这个矩阵是半正定的。
这两个条件被称之为Mercer's condition,它与一个合法的核函数互为充要条件。