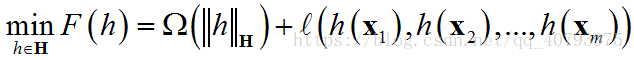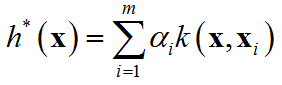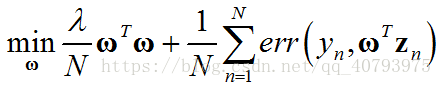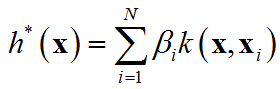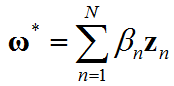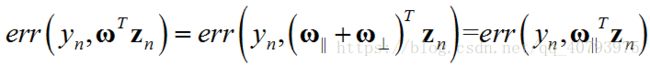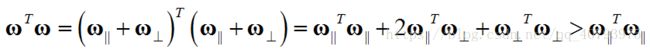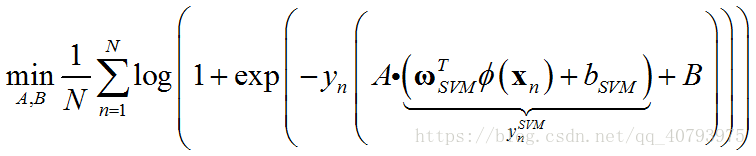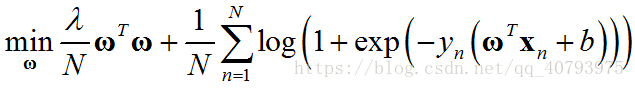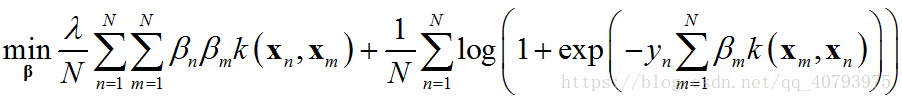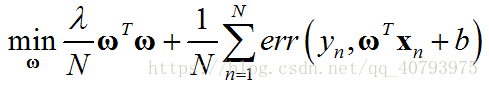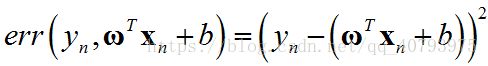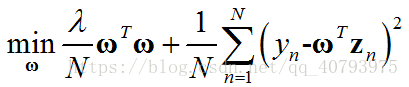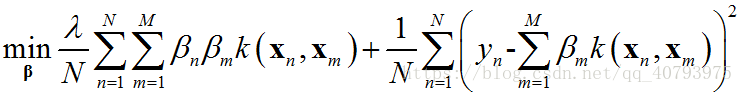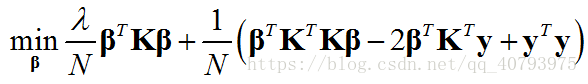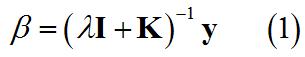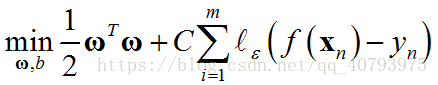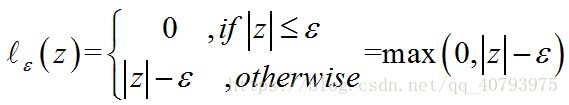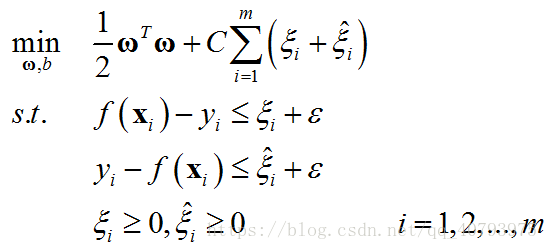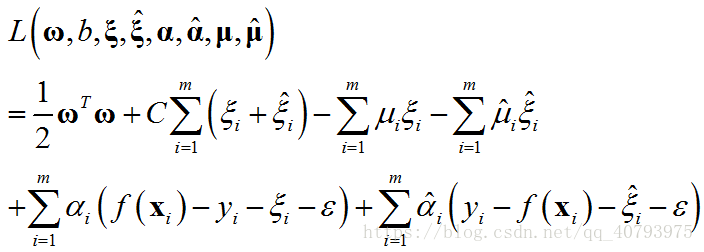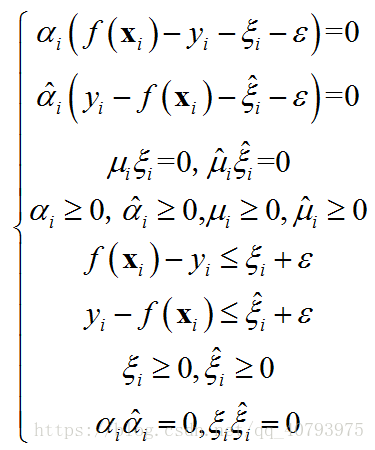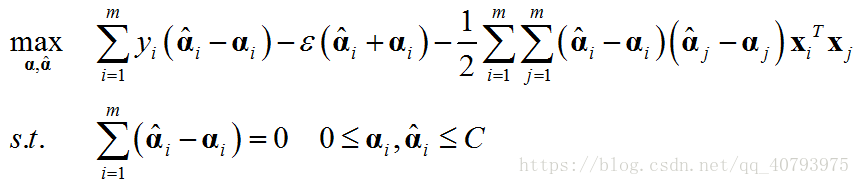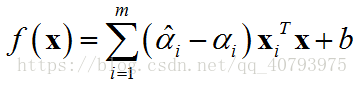核技巧（Kernel Trick）与支持向量回归（SVR）详解
核技巧（Kernel Trick）与支持向量回归（SVR）详解
第十五次写博客，本人数学基础不是太好，如果有幸能得到读者指正，感激不尽，希望能借此机会向大家学习。这一篇内容来自于《机器学习》和林轩田《技法》以及自己的一些理解。
这篇文章首先对表示定理（Representor Theorem）进行介绍和证明，然后引出核技巧（Kernel Trick）及其应用，再介绍核技巧版的线性回归即核线性回归，最后通过核线性回归和带核SVM对比引出支持向量回归（Support Vector Regression）。
表示定理（Representor Theorem）
令 H \mathbf{H} H为核函数 k k k对应的再生核希尔伯特空间（Mercer 定理中提到过）， ∣ ∣ h ∣ ∣ H ||h||_{\mathbf{H}} ∣∣h∣∣H表示 H \mathbf{H} H空间中关于优化问题的解 h h h的范数，对于任意单调递增函数 Ω : [ 0 , ∞ ] ↦ R \Omega:[0,\infty]\mapsto{\Bbb{R}} Ω:[0,∞]↦R和任意非负损失函数 l : R m ↦ [ 0 , ∞ ] l:\Bbb{R}^m\mapsto[0,\infty] l:Rm↦[0,∞]，优化问题
的解总可写为
表示定理对损失函数没有限制，对正则化项 Ω \Omega Ω仅要求单调递增，甚至不要求 Ω \Omega Ω是凸函数，因此对于一般的损失函数和正则化项，优化问题的最优解 h ∗ ( x ) h^{*}\left(\mathbf{x}\right) h∗(x)都可以表示为核函数 k ( x , x i ) k\left(\mathbf{x},\mathbf{x}_i\right) k(x,xi)的线性组合。
下面以带有 L 2 L_2 L2正则项的线性模型为例，证明这个定理，假设该优化问题可以表示为
其中， z n = ϕ ( x n ) \mathbf{z}_n=\phi\left(\mathbf{x}_n\right) zn=ϕ(xn)，假设该问题的最优解为
最优的目标变量可以写为
证明上式成立，目标变量的一般形式可以写为 ω ∗ = ω ∣ ∣ + ω ⊥ \omega^*=\omega_{||}+\omega_{\bot} ω∗=ω∣∣+ω⊥，其中， ω ∣ ∣ ∈ s p a n ( x n ) \omega_{||}\in{span\left(\mathbf{x}_n\right)} ω∣∣∈span(xn)， ω ⊥ ⊥ s p a n ( x n ) \omega_{\bot}\bot{span\left(\mathbf{x}_n\right)} ω⊥⊥span(xn)，为了得到形如上式的最优解，应该使垂直分量 ω ⊥ = 0 \omega_{\bot}=0 ω⊥=0。根据反证法，如果该分量不为零，那么优化目标中的第二项，由于 ω ⊥ ⊥ s p a n ( x n ) \omega_{\bot}\bot{span\left(\mathbf{x}_n\right)} ω⊥⊥span(xn)的原因，可以表示为
由上式可见，垂直分量对这一项并没有任何影响。对于优化目标的第一项，
由上式可见，垂直分量会增加这一项的误差，因此原定理得证。
核技巧（Kernel Trick）及其应用
由核函数可知，核技巧的本质是将数据集从原样本空间映射到更高维的空间中的同时，又不会使学习器的训练难度随维度的提高而增加，以此来达到学习器的预期设计目的，下面分别以概率支持向量机（Probabilistic SVM）和核逻辑回归（KLR）两个例子来说明核技巧的不同应用方式。
1.概率支持向量机（Probabilistic SVM）
现有一个线性不可分的数据集，为了结合带核函数的支持向量机可以将不可分数据集通过超平面（hyperplane）分开的特点，和逻辑回归的便于计算的特点。这里首先在原数据集上运行SVM算法，得到 ω S V M \omega_{SVM} ωSVM、 b S V M b_{SVM} bSVM后，利用 y n S V M = ω S V M T ϕ ( x n ) + b S V M y_n^{SVM}=\omega^{T}_{SVM}\phi\left(\mathbf{x}_n\right)+b_{SVM} ynSVM=ωSVMTϕ(xn)+bSVM，将原样本空间中的输入属性 x n \mathbf{x}_n xn转化为中的一个实数，然后，在得到的新数据集 ( y n S V M , y n ) \left(y_n^{SVM},y_n\right) (ynSVM,yn)上训练单变量的逻辑回归模型，最终得到的学习器结合了上述两个算法的特点，其中，SVM的训练中用到了核函数。
上述问题可以表示为下式
2.核逻辑回归（KLR）
带 L 2 L_2 L2正则项的逻辑回归问题可以由下式表示
假设，忽略偏置项 b b b的影响，并将原空间中的输入向量 x n \mathbf{x}_n xn映射为高维向量 z n \mathbf{z}_n zn，得到替代优化目标
那么，由表示定理可知，该问题的最优解可以表示为 ω ∗ = ∑ n = 1 N β n z n \omega^*=\sum_{n=1}^{N}\beta_n\mathbf{z}_n ω∗=∑n=1Nβnzn，现在将 ω ∗ \omega^* ω∗带入到上面优化目标中，得到
这就是由表示定理得到的KLR的目标函数，其中向量 β \beta β是优化变量，可以将上式中的第一项作为一个特殊的正则化项，第二项是模型对样本 ( ∑ m β m k ( x m , x n ) , y n ) \left(\sum_{m}\beta_{m}k\left(\mathbf{x}_m,\mathbf{x}_n\right),y_n\right) (∑mβmk(xm,xn),yn)的拟合程度，这与带核函数SVM的目标函数形式类似。需要注意的是，由于第二项选择的对率损失函数会为所有不满足 ( ∑ m β m k ( x m , x n ) ) ⋅ y n = 1 \left(\sum_{m}\beta_{m}k\left(\mathbf{x}_m,\mathbf{x}_n\right)\right)\cdot{}y_n=1 (∑mβmk(xm,xn))⋅yn=1的样本点计算误差，即最后的模型考虑了训练集中的所有样本点的影响，因此，这里的协同系数 β n \beta_n βn并不稀疏，导致训练成本与训练集规模直接相关。
核线性回归（Kernel Linear Regression）
带 L 2 L_2 L2正则项的线性回归问题可以用下式表示
其中，误差度量公式采用平方误差
如果忽略偏置项 b b b的影响，并将原空间中的输入向量 x n \mathbf{x}_n xn映射为高维向量 z n \mathbf{z}_n zn，得到替代优化目标
那么，由表示定理可知，该问题的最优解可以表示为 ω ∗ = ∑ n = 1 N β n z n \omega^*=\sum_{n=1}^{N}\beta_n\mathbf{z}_n ω∗=∑n=1Nβnzn，现在将 ω ∗ \omega^* ω∗带入到上面优化目标中，得到
与核逻辑回归中的讨论类似，由于第二项选择的平方误差损失函数会为所有不满足 y n = ∑ m β m k ( x m , x n ) y_n=\sum_{m}\beta_mk\left(\mathbf{x}_m,\mathbf{x}_n\right) yn=∑mβmk(xm,xn)的样本点计算误差，即最后的模型考虑了训练集中的所有样本点的影响，因此，这里的协同系数 β n \beta_n βn并不稀疏，导致训练成本与训练集规模直接相关，这点将在下面的讨论中体现出来。
将通过表示定理得到的优化目标由向量和矩阵形式表示，可以写成
其中，向量 β \beta β为协同向量，矩阵 K \mathbf{K} K为核矩阵（SVM中提到过），这是一个无约束的优化问题，直接通过对求 β \beta β偏导并置零来求得解的形式如下
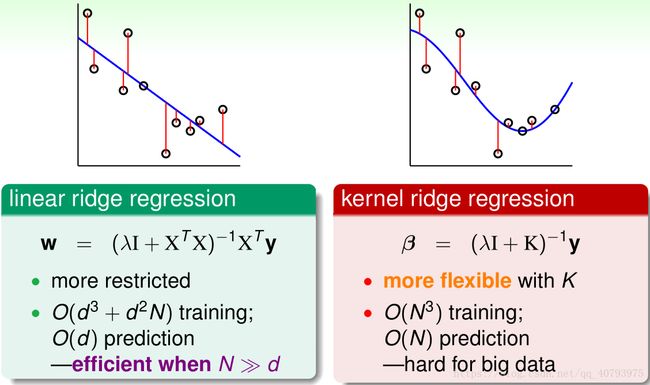
下面对核线性回归得到的回归曲线和计算复杂度进行讨论，由式（1）可以看出，核矩阵的规模为NxN，向量的规模为Nx1，最终训练的复杂度为 O ( N 3 ) O\left(N^3\right) O(N3)与数据集规模的立方成正比，这种方法得到的系数 β \beta β是稠密的，与传统的线性回归相比有如下区别
由上图所示，核线性回归得到的回归曲线更符合真实样本分布，但是随数据集大小的提高，其计算复杂度是呈立方增加的，因此不适合处理大量数据。
支持向量回归（Support Vector Regression）
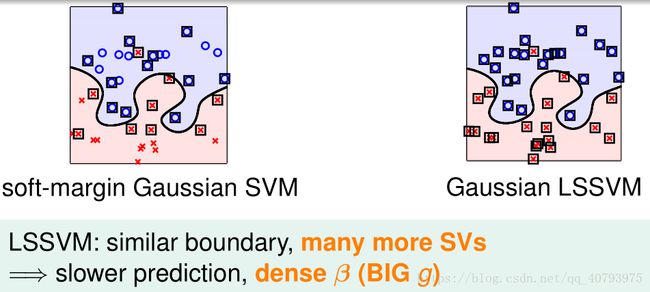
由于对输出值进行离散化处理后的线性回归可以看作是逻辑回归，因此核线性回归也可用于分类任务，由此得到的学习器可以作为最小二乘支持向量机（LSSVM）来使用，下面是LLSVM与Soft-margin SVM的区别
由上图可以看出，代表核线性回归的LSSVM算法由于协同系数是稠密的，因此最终产生的模型需要全部训练样本作为其支持向量；而带核函数的软间隔支持向量机最终产生的模型只需要一部分的原始样本点作为其支持向量，因此在模型生成之后，Soft-margin SVM的预测成本（Prediction Cost）要比LSSVM小得多。
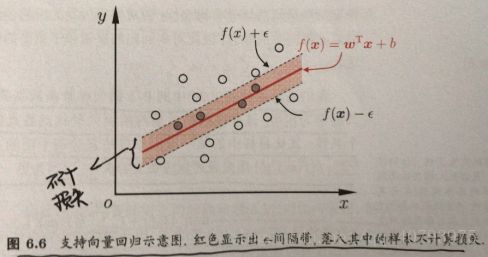
为了在保留带核函数支持向量机的优点的基础上，使其适用于回归任务，支持向量回归（SVR）由此产生，与传统带核线性回归计算每个样本误差的方式不同，SVR能容忍预测输出 f ( x n ) f\left(\mathbf{x}_n\right) f(xn)与真实输出 y n y_n yn之间最多有 ε \varepsilon ε的偏差，即当他们之间差的绝对值大于 ε \varepsilon ε时，才计算这个样本的损失，如下图所示，这相当于以预测曲线为中心，构建了一个宽度为 ε \varepsilon ε的间隔带，带中样本不计损失。
因此，SVR的优化目标可以表示为
其中， C C C为正则化常数， l ε l_\varepsilon lε被称为 ε \varepsilon ε-不敏感损失函数，表示成如下形式：
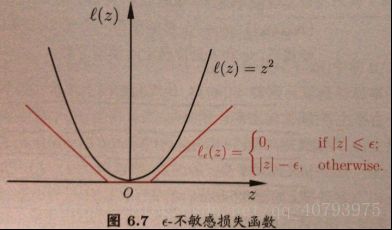
其与平方误差函数的关系如下图所示
使用不同松弛变量和来表示样本点位于预测曲线左右两边时不同的误差，优化目标可以写为
这里需要注意的是，松弛变量和至少有一个为零，因为一个点不可能同时位于预测曲线的两边，即。与软间隔支持向量机类似，上述问题的拉格朗日乘子函数为
其KKT条件为
KKT条件中的 α i α ^ i = 0 \alpha_i\hat{\alpha}_i=0 αiα^i=0由于 f ( x i ) − y i − ξ i − ε = 0 f\left(\mathbf{x}_i\right)-y_i-\xi_i-\varepsilon=0 f(xi)−yi−ξi−ε=0和 y i − f ( x i ) − ξ i − ε = 0 y_i-f\left(\mathbf{x}_i\right)-\xi_i-\varepsilon=0 yi−f(xi)−ξi−ε=0不可能同时成立，这与 ξ i ξ ^ i = 0 \xi_i\hat{\xi}_i=0 ξiξ^i=0的原因类似。与得到标准SVM的对偶问题相同，将上述拉格朗日乘子函数分别对 ω \omega ω、 b b b、 ξ i \xi_i ξi、 ξ ^ i \hat{\xi}_i ξ^i求偏导并置零，并将得到的等式重新带入乘子函数中，得到如下对偶问题
由KKT条件可知，只有当 f ( x i ) − y i − ξ i − ε = 0 f\left(\mathbf{x}_i\right)-y_i-\xi_i-\varepsilon=0 f(xi)−yi−ξi−ε=0时 α i \alpha_i αi才可能取到非零值，只有当 y i − f ( x i ) − ξ i − ε = 0 y_i-f\left(\mathbf{x}_i\right)-\xi_i-\varepsilon=0 yi−f(xi)−ξi−ε=0时 α ^ i \hat{\alpha}_i α^i才有可能取到非零值，即只有当样本点落在宽度为 ε \varepsilon ε的间隔带外面，相应的 α i \alpha_i αi和 α ^ i \hat{\alpha}_i α^i才有可能取到非零值，因为落在间隔带内部的点，其对应的松弛变量 ξ i \xi_i ξi（ ξ ^ i \hat{\xi}_i ξ^i）为零，这时上述对应等式 f ( x i ) − y i − ξ i − ε = 0 f\left(\mathbf{x}_i\right)-y_i-\xi_i-\varepsilon=0 f(xi)−yi−ξi−ε=0（ y i − f ( x i ) − ξ i − ε = 0 y_i-f\left(\mathbf{x}_i\right)-\xi_i-\varepsilon=0 yi−f(xi)−ξi−ε=0）不成立，所以 α i \alpha_i αi（ α ^ i \hat{\alpha}_i α^i）为零。最终得到的SVR的解的形式为
因此，可以作为支持向量的点，即 ( α i − α ^ i ) ≠ 0 \left(\alpha_i-\hat{\alpha}_i\right)\neq0 (αi−α^i)̸=0的点，必定位于间隔带外，这就体现了SVR的解的稀疏性。
参考资料
【1】《机器学习》周志华
【2】《机器学习技法》林轩田