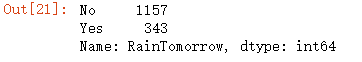sklearn实战-----8.支持向量机SVM(下)
1 二分类SVC的进阶
1.1 SVC用于二分类的原理复习
在上周的支持向量SVM(上)中,我们学习了二分类SVC的所有基本知识,包括SVM的原理,二分类SVC的损失函数,拉格朗日函数,拉格朗日对偶函数,预测函数以及这些函数在非线性,软间隔这些情况上的推广,并且引出了核函数这个关键概念。今天,基于我们已经学过的理论,我们继续探索支持向量机的其他性质,并在真实数据集上运用SVM。开始今天的探索之前,我们先来简单回忆一下支持向量机是如何工作的。

支持向量机分类器,是在数据空间中找出一个超平面作为决策边界,利用这个决策边界来对数据进行分类,并使分类误差尽量小的模型。决策边界是比所在数据空间小一维的空间,在三维数据空间中就是一个平面,在二维数据空间中就是一条直线。以二维数据为例,图中的数据集有两个特征,标签有两类,一类为紫色,一类为红色。对于这组数据,我们找出的决策边界被表达为 KaTeX parse error: Undefined control sequence: \cdotx at position 2: w\̲c̲d̲o̲t̲x̲+b=0,决策边界把平面分成了上下两部分,决策边界以上的样本都分为一类,决策边界以下的样本被分为另一类。以我们的图像为例,绿色实线上部分为一类(全部都是紫色点),下部分为另一类(全都是红色点)。
平行于决策边界的两条虚线是距离决策边界相对距离为1的超平面,他们分别压过两类样本中距离决策边界最近的样本点,这些样本点就被成为支持向量。两条虚线超平面之间的距离叫做边际,简写为 d d d。支持向量机分类器,就是以找出最大化的边际d为目标来求解损失函数,以求解出参数 w w w和 b b b ,以构建决策边界,然后用决策边界来分类的分类器。
当然,不是所有数据都是线性可分的,不是所有数据我们都能够一眼看出,有一条直线,或一个平面,甚至一个超平面可以将数据完全分开。比如下面的环形数据。对于这样的数据,我们需要对它进行一个升维变化,来数据从原始的空间 x x x投射到新空间 ϕ ( x ) \phi(x) ϕ(x)中。升维之后,我们明显可以找出一个平面,能够将数据切分开来。 ϕ \phi ϕ 是一个映射函数,它代表了某种能够将数据升维的非线性的变换,我们对数据进行这样的变换,确保数据在自己的空间中一定能够线性可分。
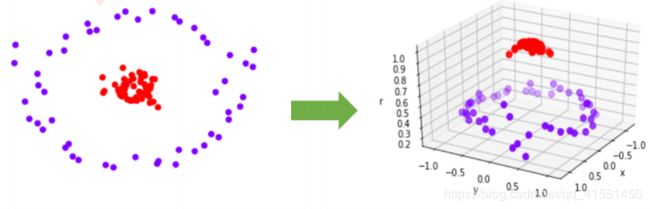
但这种手段是有问题的,我们很难去找出一个函数 ϕ ( x ) \phi(x) ϕ(x)来满足我们的需求,并且我们并不知道数据究竟被映射到了一个多少维度的空间当中,有可能数据被映射到了无限空间中,陷入“维度诅咒”,让我们的计算和预测都变得无比艰难。为了避免这些问题,我们使用核函数来帮助我们。核函数 K ( x , x t e x t ) K(x,x_{text}) K(x,xtext)能够用原始数据空间中向量计算来表示升维后地空间中的点积 ϕ ( x ) ⋅ \phi(x)\cdot ϕ(x)⋅\phi(x_{test})$$,以帮助我们避免寻找 ϕ ( x ) \phi(x) ϕ(x)。选用不同的核函数,就可以解决不同数据分布下的寻找超平面问题。在sklearn的SVC中,这个功能由参数“kernel”(ˈkərnl)和一系列与核函数相关的参数来进行控制,包括gamma,coef0和degree。同时,我们还讲解了软间隔和硬间隔中涉及到的参数C。今天我们就从参数C的进阶理解开始继续探索我们的支持向量机。
1.2 参数C的理解进阶
有一些数据,可能是线性可分,但在线性可分状况下训练准确率不能达到100%,即无法让训练误差为0,这样的数据被我们称为“存在软间隔的数据”。此时此刻,我们需要让我们决策边界能够忍受一小部分训练误差,我们就不能
单纯地寻求最大边际了。
因为对于软间隔地数据来说,边际越大被分错的样本也就会越多,因此我们需要找出一个”最大边际“与”被分错的样本数量“之间的平衡。因此,我们引入松弛系数 和松弛系数的系数C作为一个惩罚项,来惩罚我们对最大边际的追求。那我们的参数C如何影响我们的决策边界呢?在硬间隔的时候,我们的决策边界完全由两个支持向量和最小化损失函数(最大化边际)来决定,而我们的支持向量是两个标签类别不一致的点,即分别是正样本和负样本。然而在软间隔情况下我们的边际依然由支持向量决定,但此时此刻的支持向量可能就不再是来自两种标签类别的点了,而是分布在决策边界两边的,同类别的点。回忆一下我们的图像:
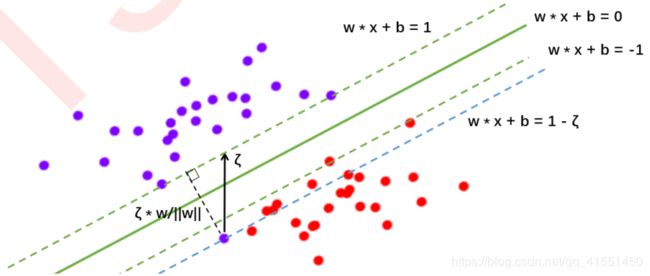
此时我们的虚线超平面 w ⋅ x i + b = 1 − ζ i w\cdot x_i+b=1-\zeta_i w⋅xi+b=1−ζi是由混杂在红色点中间的紫色点来决定的,所以此时此刻,这个紫色点就是我们的支持向量了。所以软间隔让决定两条虚线超平面的支持向量可能是来自于同一个类别的样本点,而硬间隔的时候两条虚线超平面必须是由来自两个不同类别的支持向量决定的。而C值会决定我们究竟是依赖红色点作为支持向量(只追求最大边界),还是我们要依赖软间隔中,混杂在红色点中的紫色点来作为支持向量(追求最大边界和判断正确的平衡)。如果C值设定比较大,那SVC可能会选择边际较小的,能够更好地分类所有训练点的决策边界,不过模型的训练时间也会更长。如果C的设定值较小,那SVC会尽量最大化边界,尽量将掉落在决策边界另一方的样本点预测正确,决策功能会更简单,但代价是训练的准确度,因为此时会有更多红色的点被分类错误。换句话说,C在SVM中的影响就像正则化参数对逻辑回归的影响。
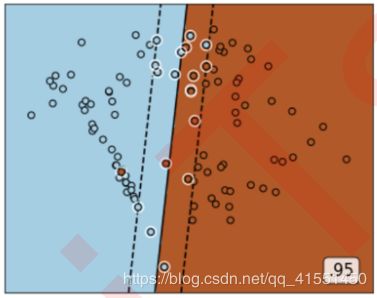
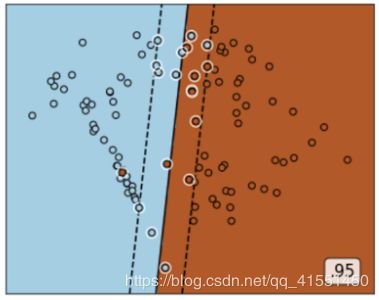
此时此刻,所有可能影响我们的超平面的样本可能都会被定义为支持向量,所以支持向量就不再是所有压在虚线超平面上的点,而是所有可能影响我们的超平面的位置的那些混杂在彼此的类别中的点了。观察一下我们对不同数据集分类时,支持向量都有哪些?软间隔如何影响了超平面和支持向量,就一目了然了。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import svm
from sklearn.datasets import make_circles, make_moons, make_blobs,make_classification
n_samples = 100
datasets = [
make_moons(n_samples=n_samples, noise=0.2, random_state=0),
make_circles(n_samples=n_samples, noise=0.2, factor=0.5, random_state=1),
make_blobs(n_samples=n_samples, centers=2, random_state=5),
make_classification(n_samples=n_samples,n_features = 2,n_informative=2,n_redundant=0, random_state=5)
]
Kernel = ["linear"]
#四个数据集分别是什么样子呢?
for X,Y in datasets:
plt.figure(figsize=(5,4))
plt.scatter(X[:,0],X[:,1],c=Y,s=50,cmap="rainbow")
nrows=len(datasets)
ncols=len(Kernel) + 1
fig, axes = plt.subplots(nrows, ncols,figsize=(10,16))
#第一层循环:在不同的数据集中循环
for ds_cnt, (X,Y) in enumerate(datasets):
#在图像中的第一列,放置原数据的分布
ax = axes[ds_cnt, 0]
if ds_cnt == 0:
ax.set_title("Input data")
ax.scatter(X[:, 0], X[:, 1], c=Y, zorder=10, cmap=plt.cm.Paired,edgecolors='k')
ax.set_xticks(())
ax.set_yticks(())
#第二层循环:在不同的核函数中循环
#从图像的第二列开始,一个个填充分类结果
for est_idx, kernel in enumerate(Kernel):
#定义子图位置
ax = axes[ds_cnt, est_idx + 1]
#建模
clf = svm.SVC(kernel=kernel, gamma=2).fit(X, Y)
score = clf.score(X, Y)
#绘制图像本身分布的散点图
ax.scatter(X[:, 0], X[:, 1], c=Y
,zorder=10
,cmap=plt.cm.Paired,edgecolors='k')
#绘制支持向量
ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=100,
facecolors='none', zorder=10, edgecolors='white')
#绘制决策边界
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
#np.mgrid,合并了我们之前使用的np.linspace和np.meshgrid的用法
#一次性使用最大值和最小值来生成网格
#表示为[起始值:结束值:步长]
#如果步长是复数,则其整数部分就是起始值和结束值之间创建的点的数量,并且结束值被包含在内
XX, YY = np.mgrid[x_min:x_max:200j, y_min:y_max:200j]
#np.c_,类似于np.vstack的功能
Z = clf.decision_function(np.c_[XX.ravel(), YY.ravel()]).reshape(XX.shape)
#填充等高线不同区域的颜色
ax.pcolormesh(XX, YY, Z > 0, cmap=plt.cm.Paired)
#绘制等高线
ax.contour(XX, YY, Z, colors=['k', 'k', 'k'], linestyles=['--', '-', '--'],
levels=[-1, 0, 1])
#设定坐标轴为不显示
ax.set_xticks(())
ax.set_yticks(())
#将标题放在第一行的顶上
if ds_cnt == 0:
ax.set_title(kernel)
#为每张图添加分类的分数
ax.text(0.95, 0.06, ('%.2f' % score).lstrip('0')
, size=15
, bbox=dict(boxstyle='round', alpha=0.8, facecolor='white')
#为分数添加一个白色的格子作为底色
, transform=ax.transAxes #确定文字所对应的坐标轴,就是ax子图的坐标轴本身
, horizontalalignment='right' #位于坐标轴的什么方向
)
plt.tight_layout()
plt.show()
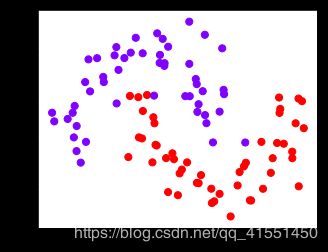
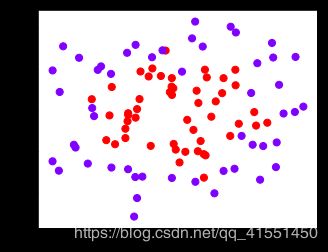
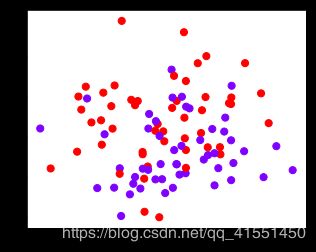
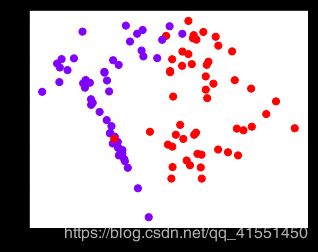

白色圈圈出的就是我们的支持向量,大家可以看到,所有在两条虚线超平面之间的点,和虚线超平面外,但属于另一个类别的点,都被我们认为是支持向量。并不是因为这些点都在我们的超平面上,而是因为我们的超平面由所有的这些点来决定,我们可以通过调节C来移动我们的超平面,让超平面过任何一个白色圈圈出的点。参数C就是这样影响了我们的决策,可以说是彻底改变了支持向量机的决策过程。
1.3 二分类SVC中的样本不均衡问题:重要参数class_weight
对于分类问题,永远都逃不过的一个痛点就是样本不均衡问题。样本不均衡是指在一组数据集中,标签的一类天生占有很大的比例,但我们有着捕捉出某种特定的分类的需求的状况。比如,我们现在要对潜在犯罪者和普通人进行分类,潜在犯罪者占总人口的比例是相当低的,也许只有2%左右,98%的人都是普通人,而我们的目标是要捕获出潜在犯罪者。这样的标签分布会带来许多问题。
首先,分类模型天生会倾向于多数的类,让多数类更容易被判断正确,少数类被牺牲掉。因为对于模型而言,样本量越大的标签可以学习的信息越多,算法就会更加依赖于从多数类中学到的信息来进行判断。如果我们希望捕获少数类,模型就会失败。其次,模型评估指标会失去意义。这种分类状况下,即便模型什么也不做,全把所有人都当成不会犯罪的人,准确率也能非常高,这使得模型评估指标accuracy变得毫无意义,根本无法达到我们的“要识别出会犯罪的人”的建模目的。
所以现在,我们首先要让算法意识到数据的标签是不均衡的,通过施加一些惩罚或者改变样本本身,来让模型向着捕获少数类的方向建模。然后,我们要改进我们的模型评估指标,使用更加针对于少数类的指标来优化模型。
要解决第一个问题,我们在逻辑回归中已经介绍了一些基本方法,比如上采样下采样。但这些采样方法会增加样本的总数,对于支持向量机这个样本总是对计算速度影响巨大的算法来说,我们完全不想轻易地增加样本数量。况且,支持向量机中地决策仅仅决策边界的影响,而决策边界又仅仅受到参数C和支持向量的影响,单纯地增加样本数量不仅会增加计算时间,可能还会增加无数对决策边界无影响的样本点。因此在支持向量机中,我们要大力依赖我们调节样本均衡的参数:SVC类中的class_weight和接口fit中可以设定的sample_weight。
在逻辑回归中,参数class_weight默认None,此模式表示假设数据集中的所有标签是均衡的,即自动认为标签的比例是1:1。所以当样本不均衡的时候,我们可以使用形如{“标签的值1”:权重1,“标签的值2”:权重2}的字典来输入真实的样本标签比例,来让算法意识到样本是不平衡的。或者使用”balanced“模式,直接使用n_samples/(n_classes * np.bincount(y))作为权重,可以比较好地修正我们的样本不均衡情况。
但在SVM中,我们的分类判断是基于决策边界的,而最终决定究竟使用怎样的支持向量和决策边界的参数是参数C,所以所有的样本均衡都是通过参数C来调整的。
SVC的参数:class_weight
可输入字典或者"balanced”,可不填,默认None 对SVC,将类i的参数C设置为class_weight [i] * C。如果没有给出具体的class_weight,则所有类都被假设为占有相同的权重1,模型会根据数据原本的状况去训练。如果希望改善样本不均衡状况,请输入形如{“标签的值1”:权重1,“标签的值2”:权重2}的字典,则参数C将会自动被设为:
标签的值1的C:权重1 * C,标签的值2的C:权重2*C
或者,可以使用“balanced”模式,这个模式使用y的值自动调整与输入数据中的类频率成反比的权重为n_samples/(n_classes * np.bincount(y)
SVC的接口fit的参数:sample_weight
数组,结构为 (n_samples, ),必须对应输入fit中的特征矩阵的每个样本
每个样本在fit时的权重,让权重 * 每个样本对应的C值来迫使分类器强调设定的权重更大的样本。通常,较大的权重加在少数类的样本上,以迫使模型向着少数类的方向建模
通常来说,这两个参数我们只选取一个来设置。如果我们同时设置了两个参数,则C会同时受到两个参数的影响,即 class_weight中设定的权重 * sample_weight中设定的权重 * C。
我们接下来就来看看如何使用这个参数。
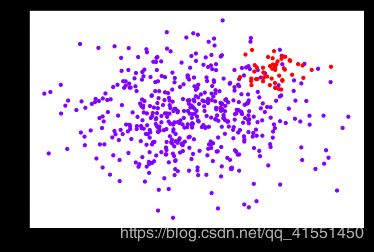
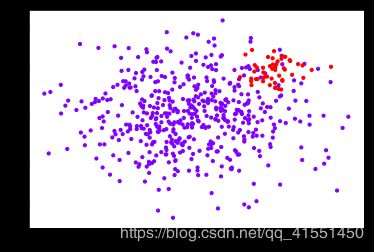
首先,我们来自建一组样本不平衡的数据集。我们在这组数据集上建两个SVC模型,一个设置有class_weight参数,一个不设置class_weight参数。我们对两个模型分别进行评估并画出他们的决策边界,以此来观察class_weight带来的效果。
- 导入需要的库和模块
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_blobs
- 创建样本不均衡的数据集
class_1 = 500 #类别1有500个样本,10:1
class_2 = 50 #类别2只有50个
centers = [[0.0, 0.0], [2.0, 2.0]] #设定两个类别的中心
clusters_std = [1.5, 0.5] #设定两个类别的方差,通常来说,样本量比较大的类别会更加松散
X, y = make_blobs(n_samples=[class_1, class_2],
centers=centers,
cluster_std=clusters_std,
random_state=0, shuffle=False)
#看看数据集长什么样
plt.scatter(X[:, 0], X[:, 1], c=y, cmap="rainbow",s=10)
plt.show()
#其中红色点是少数类,紫色点是多数类
- 在数据集上分别建模
#不设定class_weight
clf = svm.SVC(kernel='linear', C=1.0)
clf.fit(X, y)
#设定class_weight
wclf = svm.SVC(kernel='linear', class_weight={1: 10})
wclf.fit(X, y)
#给两个模型分别打分看看,这个分数是accuracy准确度
#做样本均衡之后,我们的准确率下降了,没有样本均衡的准确率更高
clf.score(X,y)
wclf.score(X,y)
0.9127272727272727
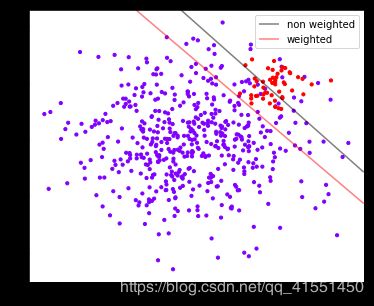
- 绘制两个模型下数据的决策边界
还记得决策边界如何绘制的么?我们利用Contour函数来帮助我们。Contour是专门用来绘制等高线的函数。等高线,本质上是在二维图像上表现三维图像的一种形式,其中两维X和Y是两条坐标轴上的取值,而Z表示高度。
Contour就是将由X和Y构成平面上的所有点中,高度一致的点连接成线段的函数,在同一条等高线上的点一定具有相同的Z值。回忆一下,我们的决策边界是 w ⋅ x + b = 0 w\cdot x+b=0 w⋅x+b=0,并在决策边界的两边找出两个超平面,使得超平面到决策边界的相对距离为1。那其实,我们只需要在我们的样本构成的平面上,把所有到决策边界的距离为0的点相连,就是我们的决策边界。而到决策边界的距离可以使用我们说明过的接口decision_function来调用。
#首先要有数据分布
plt.figure(figsize=(6,5))
plt.scatter(X[:, 0], X[:, 1], c=y, cmap="rainbow",s=10)
ax = plt.gca() #获取当前的子图,如果不存在,则创建新的子图
#绘制决策边界的第一步:要有网格
xlim = ax.get_xlim()
ylim = ax.get_ylim()
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
#第二步:找出我们的样本点到决策边界的距离
Z_clf = clf.decision_function(xy).reshape(XX.shape)
a = ax.contour(XX, YY, Z_clf, colors='black', levels=[0], alpha=0.5, linestyles=['-'])
Z_wclf = wclf.decision_function(xy).reshape(XX.shape)
b = ax.contour(XX, YY, Z_wclf, colors='red', levels=[0], alpha=0.5, linestyles=['-'])
#第三步:画图例
plt.legend([a.collections[0], b.collections[0]], ["non weighted", "weighted"],
loc="upper right")
plt.show()
a.collections #调用这个等高线对象中画的所有线,返回一个惰性对象
#用[*]把它打开试试看
[*a.collections] #返回了一个linecollection对象,其实就是我们等高线里所有的线的列表
#现在我们只有一条线,所以我们可以使用索引0来锁定这个对象
a.collections[0]
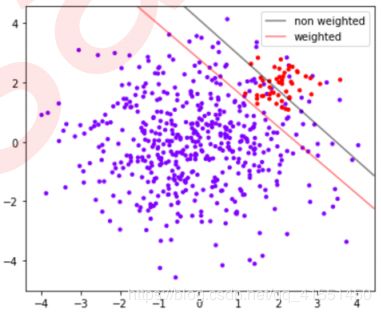
从图像上可以看出,灰色是我们做样本平衡之前的决策边界。灰色线上方的点被分为一类,下方的点被分为另一类。可以看到,大约有一半少数类(红色)被分错,多数类(紫色点)几乎都被分类正确了。红色是我们做样本平衡之后的决策边界,同样是红色线上方一类,红色线下方一类。可以看到,做了样本平衡后,少数类几乎全部都被分类正确了,但是多数类有许多被分错了。我们来看看两种情况下模型的准确率如何表现:
#给两个模型分别打分看看,这个分数是accuracy准确度
#做样本均衡之后,我们的准确率下降了,没有样本均衡的准确率更高
clf.score(X, y)
wclf.score(X, y)
可以看出,从准确率的角度来看,不做样本平衡的时候准确率反而更高,做了样本平衡准确率反而变低了,这是因为做了样本平衡后,为了要更有效地捕捉出少数类,模型误伤了许多多数类样本,而多数类被分错的样本数量 > 少数类被分类正确的样本数量,使得模型整体的精确性下降。现在,如果我们的目的是模型整体的准确率,那我们就要拒绝样本平衡,使用class_weight被设置之前的模型。
然而在现实中,我们往往都在追求捕捉少数类,因为在很多情况下,将少数类判断错的代价是巨大的。比如我们之前提到的,判断潜在犯罪者和普通人的例子,如果我们没有能够识别出潜在犯罪者,那么这些人就可能去危害社会,造成恶劣影响,但如果我们把普通人错认为是潜在犯罪者,我们也许只是需要增加一些监控和人为甄别的成本。所以对我们来说,我们宁愿把普通人判错,也不想放过任何一个潜在犯罪者。我们希望不惜一切代价来捕获少数类,或者希望捕捉出尽量多的少数类,那我们就必须使用class_weight设置后的模型。
2 SVC的模型评估指标
从上一节的例子中可以看出,如果我们的目标是希望尽量捕获少数类,那准确率这个模型评估逐渐失效,所以我们需要新的模型评估指标来帮助我们。如果简单来看,其实我们只需要查看模型在少数类上的准确率就好了,只要能够将少数类尽量捕捉出来,就能够达到我们的目的。
但此时,新问题又出现了,我们对多数类判断错误后,会需要人工甄别或者更多的业务上的措施来一一排除我们判断错误的多数类,这种行为往往伴随着很高的成本。比如银行在判断”一个申请信用卡的客户是否会出现违约行为“的时候,如果一个客户被判断为”会违约“,这个客户的信用卡申请就会被驳回,如果为了捕捉出”会违约“的人,大量地将”不会违约“的客户判断为”会违约“的客户,就会有许多无辜的客户的申请被驳回。信用卡对银行来说意味着利息收入,而拒绝了许多本来不会违约的客户,对银行来说就是巨大的损失。同理,大众在召回不符合欧盟标准的汽车时,如果为了找到所有不符合标准的汽车,而将一堆本来符合标准了的汽车召回,这个成本是不可估量的。
也就是说,单纯地追求捕捉出少数类,就会成本太高,而不顾及少数类,又会无法达成模型的效果。所以在现实中,我们往往在寻找捕获少数类的能力和将多数类判错后需要付出的成本的平衡。如果一个模型在能够尽量捕获少数类的情况下,还能够尽量对多数类判断正确,则这个模型就非常优秀了。为了评估这样的能力,我们将引入新的模型评估指标:混淆矩阵和ROC曲线来帮助我们。
2.1 混淆矩阵(Confusion Matrix)
混淆矩阵是二分类问题的多维衡量指标体系,在样本不平衡时极其有用。在混淆矩阵中,我们将少数类认为是正例,多数类认为是负例。在决策树,随机森林这些普通的分类算法里,即是说少数类是1,多数类是0。在SVM里,就是说少数类是1,多数类是-1。普通的混淆矩阵,一般使用{0,1}来表示。混淆矩阵阵如其名,十分容易让人混淆,在许多教材中,混淆矩阵中各种各样的名称和定义让大家难以理解难以记忆。我为大家找出了一种简化的方式来显示标准二分类的混淆矩阵,如图所示:
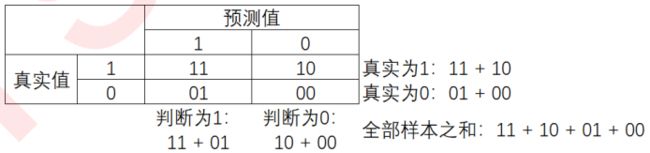
混淆矩阵中,永远是真实值在前,预测值在后。其实可以很容易看出,11和00的对角线就是全部预测正确的,01和10的对角线就是全部预测错误的。基于混淆矩阵,我们有六个不同的模型评估指标,这些评估指标的范围都在[0,1]之间,所有以11和00为分子的指标都是越接近1越好,所以以01和10为分子的指标都是越接近0越好。对于所有的指标,我们用橙色表示分母,用绿色表示分子,则我们有:
2.1.1 模型整体效果:准确率

准确率Accuracy就是所有预测正确的所有样本除以总样本,通常来说越接近1越好。
2.1.2 捕捉少数类的艺术:精确度,召回率和F1 score
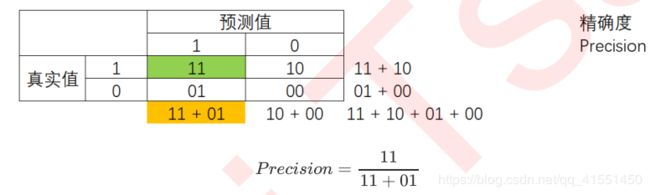
精确度Precision,又叫查准率,表示所有被我们预测为是少数类的样本中,真正的少数类所占的比例。在支持向量机中,精确度可以被形象地表示为决策边界上方的所有点中,红色点所占的比例。精确度越高,代表我们捕捉正确的红色点越多,对少数类的预测越精确。精确度越低,则代表我们误伤了过多的多数类。精确度是”将多数类判错后所需付出成本“的衡量。
#所有判断正确并确实为1的样本 / 所有被判断为1的样本
#对于没有class_weight,没有做样本平衡的灰色决策边界来说:
(y[y == clf.predict(X)] == 1).sum()/(clf.predict(X) == 1).sum()
# 0.7142857142857143
(y[y == clf.predict(X)] == 1).sum() #True = 1, False =1 #真实值等于预测值的全部点
# 30
#对于有class_weight,做了样本平衡的红色决策边界来说:
(y[y == wclf.predict(X)] == 1).sum()/(wclf.predict(X) == 1).sum()
# 0.5102040816326531
可以看出,做了样本平衡之后,精确度是下降的。因为很明显,样本平衡之后,有更多的多数类紫色点被我们误伤了。精确度可以帮助我们判断,是否每一次对少数类的预测都精确,所以又被称为”查准率“。在现实的样本不平衡例子中,当每一次将多数类判断错误的成本非常高昂的时候(比如大众召回车辆的例子),我们会追求高精确度。精确度越低,我们对多数类的判断就会越错误。当然了,如果我们的目标是不计一切代价捕获少数类,那我们并不在意精确度。
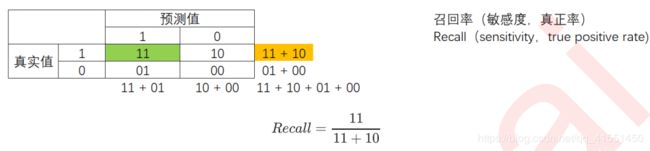
召回率Recall,又被称为敏感度(sensitivity),真正率,查全率,表示所有真实为1的样本中,被我们预测正确的样本所占的比例。在支持向量机中,召回率可以被表示为,决策边界上方的所有红色点占全部样本中的红色点的比例。召回率越高,代表我们尽量捕捉出了越多的少数类,召回率越低,代表我们没有捕捉出足够的少数类。
#所有predict为1的点 / 全部为1的点的比例
#对于没有class_weight,没有做样本平衡的灰色决策边界来说:
(y[y == clf.predict(X)] == 1).sum()/(y == 1).sum()
# 0.6
#对于有class_weight,做了样本平衡的红色决策边界来说:
(y[y == wclf.predict(X)] == 1).sum()/(y == 1).sum()
# 1.0
可以看出,做样本平衡之前,我们只成功捕获了60%左右的少数类点,而做了样本平衡之后的模型,捕捉出了100%的少数类点,从图像上来看,我们的红色决策边界的确捕捉出了全部的少数类,而灰色决策边界只捕捉到了一半左右。召回率可以帮助我们判断,我们是否捕捉除了全部的少数类,所以又叫做查全率。
如果我们希望不计一切代价,找出少数类(比如找出潜在犯罪者的例子),那我们就会追求高召回率,相反如果我们的目标不是尽量捕获少数类,那我们就不需要在意召回率。
注意召回率和精确度的分子是相同的(都是11),只是分母不同。而召回率和精确度是此消彼长的,两者之间的平衡代表了捕捉少数类的需求和尽量不要误伤多数类的需求的平衡。究竟要偏向于哪一方,取决于我们的业务需求:究竟是误伤多数类的成本更高,还是无法捕捉少数类的代价更高。
为了同时兼顾精确度和召回率,我们创造了两者的调和平均数作为考量两者平衡的综合性指标,称之为F1measure。两个数之间的调和平均倾向于靠近两个数中比较小的那一个数,因此我们追求尽量高的F1 measure,能够保证我们的精确度和召回率都比较高。F1 measure在[0,1]之间分布,越接近1越好。
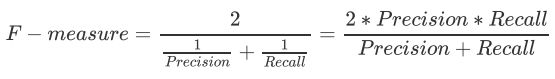
从Recall延申出来的另一个评估指标叫做假负率(False Negative Rate),它等于 1 - Recall,用于衡量所有真实为1的样本中,被我们错误判断为0的,通常用得不多。
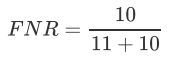
2.1.3 判错多数类的考量:特异度与假正率
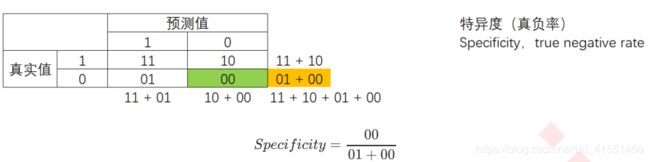
特异度(Specificity)表示所有真实为0的样本中,被正确预测为0的样本所占的比例。在支持向量机中,可以形象地表示为,决策边界下方的点占所有紫色点的比例。
#所有被正确预测为0的样本 / 所有的0样本
#对于没有class_weight,没有做样本平衡的灰色决策边界来说:
(y[y == clf.predict(X)] == 0).sum()/(y == 0).sum()
# 0.976
#对于有class_weight,做了样本平衡的红色决策边界来说:
(y[y == wclf.predict(X)] == 0).sum()/(y == 0).sum()
# 0.904
特异度衡量了一个模型将多数类判断正确的能力,而1 - specificity就是一个模型将多数类判断错误的能力,这种能力被计算如下,并叫做假正率(False Positive Rate):
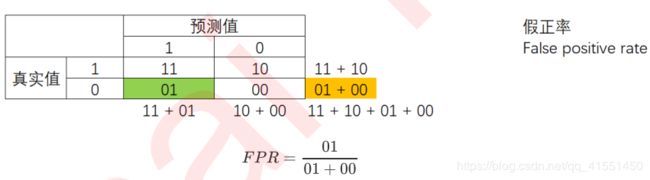
在支持向量机中,假正率就是决策边界上方的紫色点(所有被判断错误的多数类)占所有紫色点的比例。根据我们之前在precision处的分析,其实可以看得出来,当样本均衡过后,假正率会更高,因为有更多紫色点被判断错误,而样本均衡之前,假正率比较低,被判错的紫色点比较少。所以假正率其实类似于Precision的反向指标,Precision衡量有多少少数点被判断正确,而假正率FPR衡量有多少多数点被判断错误,性质是十分类似的。
2.1.4 sklearn中的混淆矩阵
sklearn当中提供了大量的类来帮助我们了解和使用混淆矩阵。
| 类 | 含义 |
|---|---|
| sklearn.metrics.confusion_matrix | 混淆矩阵 |
| sklearn.metrics.accuracy_score | 准确率accuracy |
| sklearn.metrics.precision_score | 精确度precision |
| sklearn.metrics.recall_score | 召回率recall |
| sklearn.metrics.precision_recall_curve | 精确度-召回率平衡曲线 |
| sklearn.metrics.f1_score | F1 measure |
2.2 ROC曲线以及其相关问题
基于混淆矩阵,我们学习了总共六个指标:准确率Accuracy,精确度Precision,召回率Recall,精确度和召回度的平衡指标F measure,特异度Specificity,以及假正率FPR。
其中,假正率有一个非常重要的应用:我们在追求较高的Recall的时候,Precision会下降,就是说随着更多的少数类被捕捉出来,会有更多的多数类被判断错误,但我们很好奇,随着Recall的逐渐增加,模型将多数类判断错误的
能力如何变化呢?我们希望理解,我每判断正确一个少数类,就有多少个多数类会被判断错误。假正率正好可以帮助我们衡量这个能力的变化。相对的,Precision无法判断这些判断错误的多数类在全部多数类中究竟占多大的比例,所以无法在提升Recall的过程中也顾及到模型整体的Accuracy。因此,我们可以使用Recall和FPR之间的平衡,来替代Recall和Precision之间的平衡,让我们衡量模型在尽量捕捉少数类的时候,误伤多数类的情况如何变化,这就是我们的ROC曲线衡量的平衡。
ROC曲线,全称The Receiver Operating Characteristic Curve,译为受试者操作特性曲线。这是一条以不同阈值下的假正率FPR为横坐标,不同阈值下的召回率Recall为纵坐标的曲线。让我们先从概率和阈值开始讲起。
2.2.1 概率(probability)与阈值(threshold)
要理解概率与阈值,最容易的状况是来回忆一下我们用逻辑回归做分类的时候的状况。逻辑回归的predict_proba接口对每个样本生成每个标签类别下的似然(类概率)。对于这些似然,逻辑回归天然规定,当一个样本所对应的这个标签类别下的似然大于0.5的时候,这个样本就被分为这一类。比如说,一个样本在标签1下的似然是0.6,在标签0下的似然是0.4,则这个样本的标签自然就被分为1。逻辑回归的回归值本身,其实也就是标签1下的似然。在这个过程中,0.5就被称为阈值。来看看下面的例子:
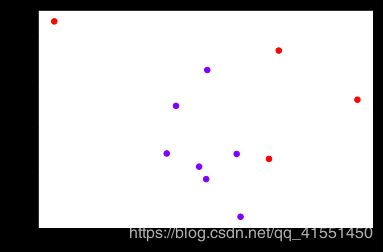
- 自建数据集
class_1_ = 7
class_2_ = 4
centers_ = [[0.0, 0.0], [1,1]]
clusters_std = [0.5, 1]
X_, y_ = make_blobs(n_samples=[class_1_, class_2_],
centers=centers_,
cluster_std=clusters_std,
random_state=0, shuffle=False)
plt.scatter(X_[:, 0], X_[:, 1], c=y_, cmap="rainbow",s=30)
plt.show()
- 建模,调用概率
from sklearn.linear_model import LogisticRegression as LogiR
clf_lo = LogiR().fit(X_,y_)
prob = clf_lo.predict_proba(X_)
#将样本和概率放到一个DataFrame中
import pandas as pd
prob = pd.DataFrame(prob)
prob.columns = ["0","1"]
prob
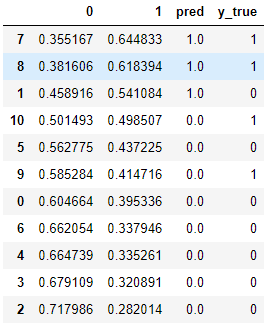
- 使用阈值0.5,大于0.5的样本被预测为1,小于0.5的样本被预测为0
#手动调节阈值,来改变我们的模型效果
for i in range(prob.shape[0]):
if prob.loc[i,"1"] > 0.5:
prob.loc[i,"pred"] = 1
else:
prob.loc[i,"pred"] = 0
prob["y_true"] = y_
prob = prob.sort_values(by="1",ascending=False)
prob
- 使用混淆矩阵查看结果
from sklearn.metrics import confusion_matrix as CM, precision_score as P, recall_score as R
CM(prob.loc[:,"y_true"],prob.loc[:,"pred"],labels=[1,0])
#试试看手动计算Precision和Recall?
P(prob.loc[:,"y_true"],prob.loc[:,"pred"],labels=[1,0])
R(prob.loc[:,"y_true"],prob.loc[:,"pred"],labels=[1,0])
- 假如我们使用0.4作为阈值呢?
for i in range(prob.shape[0]):
if prob.loc[i,"1"] > 0.4:
prob.loc[i,"pred"] = 1
else:
prob.loc[i,"pred"] = 0
CM(prob.loc[:,"y_true"],prob.loc[:,"pred"],labels=[1,0])
P(prob.loc[:,"y_true"],prob.loc[:,"pred"],labels=[1,0])
R(prob.loc[:,"y_true"],prob.loc[:,"pred"],labels=[1,0])
#注意,降低或者升高阈值并不一定能够让模型的效果变好,一切都基于我们要追求怎样的模型效果
#通常来说,降低阈值能够升高Recall
可见,在不同阈值下,我们的模型评估指标会发生变化,我们正利用这一点来观察Recall和FPR之间如何互相影响。但是注意,并不是升高阈值,就一定能够增加或者减少Recall,一切要根据数据的实际分布来进行判断。而要体现阈值的影响,首先必须的得到分类器在少数类下的预测概率。对于逻辑回归这样天生生成似然的算法和朴素贝叶斯这样就是在计算概率的算法,自然非常容易得到概率,但对于一些其他的分类算法,比如决策树,比如SVM,他们的分类方式和概率并不相关。那在他们身上,我们就无法画ROC曲线了吗?并非如此。
决策树有叶子节点,一个叶子节点上可能包含着不同类的样本。假设一个样本被包含在叶子节点a中,节点a包含10个样本,其中6个为1,4个为0,则1这个正类在这个叶子节点中的出现概率就是60%,类别0在这个叶子节点中的出现概率就是40%。对于所有在这个叶子节点中的样本而言,节点上的1和0出现的概率,就是这个样本对应的取到1和0的概率,大家可以去自己验证一下。但是思考一个问题,由于决策树可以被画得很深,在足够深的情况下,决策树的每个叶子节点上可能都不包含多个类别的标签了,可能一片叶子中只有唯一的一个标签,即叶子节点的不纯度为0,此时此刻,对于每个样本而言,他们所对应的“概率”就是0或者1了。这个时候,我们就无法调节阈值来调节我们的Recall和FPR了。对于随机森林,也是如此。
所以,如果我们有概率需求,我们还是会优先追求逻辑回归或者朴素贝叶斯。不过其实,SVM也可以生成概率,我们一起来看看,它是怎么做的。
2.2.2 SVM实现概率预测:重要参数probability,接口predict_proba以及decision_function
我们在画等高线,也就是决策边界的时候曾经使用SVC的接口decision_function,它返回我们输入的特征矩阵中每个样本到划分数据集的超平面的距离。我们在SVM中利用超平面来判断我们的样本,本质上来说,当两个点的距离是相同的符号的时候,越远离超平面的样本点归属于某个标签类的概率就很大。比如说,一个距离超平面0.1的点,和一个距离超平面100的点,明显是距离为0.1的点更有可能是负类别的点混入了边界。同理,一个距离超平面距离为-0.1的点,和一个离超平面距离为-100的点,明显是-100的点的标签更有可能是负类。所以,到超平面的距离一定程度上反应了样本归属于某个标签类的可能性。接口decision_function返回的值也因此被我们认为是SVM中的置信度(confidence)
不过,置信度始终不是概率,它没有边界,可以无限大,大部分时候也不是以百分比或者小数的形式呈现,而SVC的判断过程又不像决策树一样可以求解出一个比例。为了解决这个矛盾,SVC有重要参数probability。
| 参数 | 含义 | | ----------- | ------------------------------------------------------------ | | probability | 布尔值,可不填,默认
False
是否启用概率估计。进行必须在调用fit之前启用它,启用此功能会减慢SVM的运算速度。
设置为True则会启动,启用之后,SVC的接口predict_proba和predict_log_proba将生效。在二分类情况下,SVC将使用Platt缩放来生成概率,即在decision_function生成的距离上进行Sigmoid压缩,并附加训练数据的交叉验证拟合,来生成类逻辑回归的SVM分数。
在多分类状况下,参考Wu et al. (2004)发表的文章来将二分类情况推广到多分类。
- |Wu, Lin and Weng, “Probability estimates for multi-class classification by pairwise coupling”, JMLR5:975-1005, 2004.
来实现一下我们的概率预测吧:
#使用最初的X和y,样本不均衡的这个模型
class_1 = 500 #类别1有500个样本
class_2 = 50 #类别2只有50个
centers = [[0.0, 0.0], [2.0, 2.0]] #设定两个类别的中心
clusters_std = [1.5, 0.5] #设定两个类别的方差,通常来说,样本量比较大的类别会更加松散
X, y = make_blobs(n_samples=[class_1, class_2],
centers=centers,
cluster_std=clusters_std,
random_state=0, shuffle=False)
#看看数据集长什么样
plt.scatter(X[:, 0], X[:, 1], c=y, cmap="rainbow",s=10)
#其中红色点是少数类,紫色点是多数类
clf_proba = svm.SVC(kernel="linear",C=1.0,probability=True).fit(X,y)
clf_proba.predict_proba(X).shape #生成的各类标签下的概率
# (550, 2)
clf_proba.decision_function(X)
clf_proba.decision_function(X).shape
# (550,)
值得注意的是,在二分类过程中,decision_function只会生成一列距离,样本的类别由距离的符号来判断,但是predict_proba会生成两个类别分别对应的概率。SVM也可以生成概率,所以我们可以使用和逻辑回归同样的方式来在SVM上设定和调节我们的阈值。
毋庸置疑,Platt缩放中涉及的交叉验证对于大型数据集来说非常昂贵,计算会非常缓慢。另外,由于Platt缩放的理论原因,在二分类过程中,有可能出现predict_proba返回的概率小于0.5,但样本依旧被标记为正类的情况出现,
毕竟支持向量机本身并不依赖于概率来完成自己的分类。如果我们的确需要置信度分数,但不一定非要是概率形式的话,那建议可以将probability设置为False,使用decision_function这个接口而不是predict_proba。
2.2.3 绘制SVM的ROC曲线
现在,我们理解了什么是阈值(threshold),了解了不同阈值会让混淆矩阵产生变化,也了解了如何从我们的分类算法中获取概率。现在,我们就可以开始画我们的ROC曲线了。ROC是一条以不同阈值下的假正率FPR为横坐标,不同阈值下的召回率Recall为纵坐标的曲线。简单地来说,只要我们有数据和模型,我们就可以在python中绘制出我们的ROC曲线。思考一下,我们要绘制ROC曲线,就必须在我们的数据中去不断调节阈值,不断求解混淆矩阵,然后不断获得我们的横坐标和纵坐标,最后才能够将曲线绘制出来。接下来,我们就来执行这个过程:
#首先来看看如何从混淆矩阵中获取FPR和Recall
cm = CM(prob.loc[:,"y_true"],prob.loc[:,"pred"],labels=[1,0])
cm
#00/all true 0 1-特异度
#FPR #被我们预测错误的0占所有真正为0的样本的比例
cm[1,0]/cm[1,:].sum()
# 0.2857142857142857
#Recall
cm[0,0]/cm[0,:].sum()
# 1.0
#概率 clf_proba.predict_proba(X)[:,1] #我的类别1下面的概率
#阈值,每一个阈值都对应着一次循环,每一次循环,都要有一个混淆矩阵,要有一组假正率vsRecall
#np.lispance(概率最小值,概率最大值,55,endpoint=False) #不要取到最大值
#if i > 概率最大值, 返回1
#开始绘图
probrange = np.linspace(clf_proba.predict_proba(X)[:,1].min(),clf_proba.predict_proba(X)[:,1].max(),num=50,endpoint=False)
from sklearn.metrics import confusion_matrix as CM, recall_score as R
import matplotlib.pyplot as plot
recall = []
FPR = []
for i in probrange:
y_predict = []
for j in range(X.shape[0]):
if clf_proba.predict_proba(X)[j,1] > i:
y_predict.append(1)
else:
y_predict.append(0)
cm = CM(y,y_predict,labels=[1,0])
recall.append(cm[0,0]/cm[0,:].sum())
FPR.append(cm[1,0]/cm[1,:].sum())
recall.sort()
FPR.sort()
plt.plot(FPR,recall,c="red")
plt.plot(probrange+0.05,probrange+0.05,c="black",linestyle="--")
plt.show()

现在我们就画出了ROC曲线了,那我们如何理解这条曲线呢?先来回忆一下,我们建立ROC曲线的根本目的是找寻Recall和FPR之间的平衡,让我们能够衡量模型在尽量捕捉少数类的时候,误伤多数类的情况会如何变化。横坐标是FPR,代表着模型将多数类判断错误的能力,纵坐标Recall,代表着模型捕捉少数类的能力,所以ROC曲线代表着,随着Recall的不断增加,FPR如何增加。我们希望随着Recall的不断提升,FPR增加得越慢越好,这说明我们可以尽量高效地捕捉出少数类,而不会将很多地多数类判断错误。所以,我们希望看到的图像是,纵坐标急速上升,横坐标缓慢增长,也就是在整个图像左上方的一条弧线。这代表模型的效果很不错,拥有较好的捕获少数类的能力。
中间的虚线代表着,当recall增加1%,我们的FPR也增加1%,也就是说,我们每捕捉出一个少数类,就会有一个多数类被判错,这种情况下,模型的效果就不好,这种模型捕获少数类的结果,会让许多多数类被误伤,从而增加我们的成本。ROC曲线通常都是凸型的。对于一条凸型ROC曲线来说,曲线越靠近左上角越好,越往下越糟糕,曲线如果在虚线的下方,则证明模型完全无法使用。但是它也有可能是一条凹形的ROC曲线。对于一条凹型ROC曲线来说,应该越靠近右下角越好,凹形曲线代表模型的预测结果与真实情况完全相反,那也不算非常糟糕,只要我们手动将模型的结果逆转,就可以得到一条左上方的弧线了。最糟糕的就是,无论曲线是凹形还是凸型,曲线位于图像中间,和虚线非常靠近,那我们拿它无能为力。
好了,现在我们有了这条曲线,我们的确知道模型的效果还算是不错了。但依然非常摸棱两可,有没有具体的数字来帮助我们理解ROC曲线和模型的效果呢?的确存在,这个数字就叫做AUC面积,它代表了ROC曲线下方的面积,这个面积越大,代表ROC曲线越接近左上角,模型就越好。AUC面积的计算比较繁琐,因此,我们使用sklearn来帮助我们。接下来我们来看看,在sklearn当中,如何绘制我们的ROC曲线,找出我们的的AUC面积。
2.2.4 sklearn中的ROC曲线和AUC面积
在sklearn中,我们有帮助我们计算ROC曲线的横坐标假正率FPR,纵坐标Recall和对应的阈值的类sklearn.metrics.roc_curve。同时,我们还有帮助我们计算AUC面积的类sklearn.metrics.roc_auc_score。在一些比较老旧的sklearn版本中,我们使用sklearn.metrics.auc这个类来计算AUC面积,但这个类即将在0.22版本中被放弃,因此建议大家都使用roc_auc_score。来看看我们的这两个类:
sklearn.metrics.roc_curve (y_true, y_score, pos_label=None,
sample_weight=None, drop_intermediate=True)
y_true : 数组,形状 = [n_samples],真实标签
y_score : 数组,形状 = [n_samples],置信度分数,可以是正类样本的概率值,或置信度分数,或者decision_function返回的距离
pos_label : 整数或者字符串, 默认None,表示被认为是正类样本的类别
sample_weight : 形如 [n_samples]的类数组结构,可不填,表示样本的权重
drop_intermediate : 布尔值,默认True,如果设置为True,表示会舍弃一些ROC曲线上不显示的阈值点,这对于计算一个比较轻量的ROC曲线来说非常有用
这个类以此返回:FPR,Recall以及阈值。
来看看我们如何使用:
from sklearn.metrics import roc_curve
FPR, recall, thresholds = roc_curve(y,clf_proba.decision_function(X), pos_label=1)
FPR.shape
# (45,)
recall.shape
# (45,)
thresholds.shape #此时的threshold就不是一个概率值,而是距离值中的阈值了,所以它可以大于1,也可以为负
# (45,)
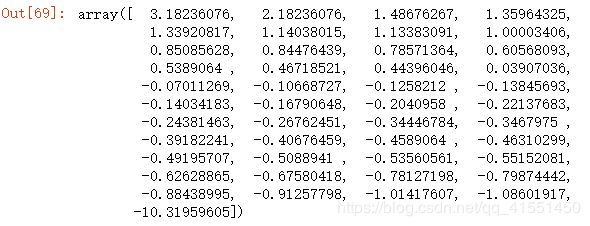
thresholds #decision_function
sklearn.metrics.roc_auc_score (y_true, y_score, average=’macro’, sample_weight=None, max_fpr=None)
AUC面积的分数使用以上类来进行计算,输入的参数也比较简单,就是真实标签,和与roc_curve中一致的置信度分数或者概率值。
from sklearn.metrics import roc_auc_score as AUC
area = AUC(y,clf_proba.decision_function(X))
接下来就可以开始画图了:
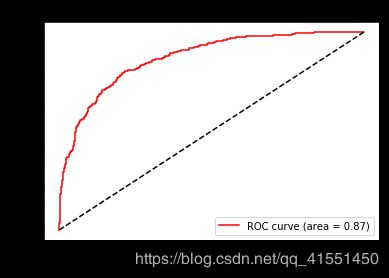
plt.figure()
plt.plot(FPR, recall, color='red',
label='ROC curve (area = %0.2f)' % area)
plt.plot([0, 1], [0, 1], color='black',linestyle='--')
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('Recall')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()
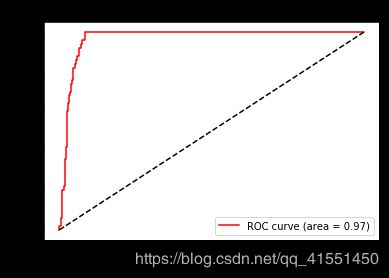
如此就得到了我们的ROC曲线和AUC面积,可以看到,SVM在这个简单数据集上的效果还是非常好的。并且大家可以通过观察我们使用decision_function画出的ROC曲线,对比一下我们之前强行使用概率画出来的曲线,两者非常相似,所以在无法获取模型概率的情况下,其实不必强行使用概率,如果有置信度,那也使可以完成我们的ROC曲线的。感兴趣的小伙伴可以画一下如果带上class_weight这个参数,模型的效果会变得如何。
2.2.5 利用ROC曲线找出最佳阈值
现在,有了ROC曲线,了解了模型的分类效力,以及面对样本不均衡问题时的效力,那我们如何求解我们最佳的阈值呢?我们想要了解,什么样的状况下我们的模型的效果才是最好的。回到我们对ROC曲线的理解来:ROC曲线反应的是recall增加的时候FPR如何变化,也就是当模型捕获少数类的能力变强的时候,会误伤多数类的情况是否严重。我们的希望是,模型在捕获少数类的能力变强的时候,尽量不误伤多数类,也就是说,随着recall的变大,FPR的大小越小越好。所以我们希望找到的最有点,其实是Recall和FPR差距最大的点。这个点,又叫做约登指数。
max((recall - FPR).tolist())
# 0.914
#lits.index(最大值) #返回这个最大值在list中的索引
maxindex = (recall - FPR).tolist().index(max(recall - FPR))
maxindex #recall, FPR
# 43
thresholds[maxindex] #decision_function生成的置信度来说
# -1.0860191749391461
#我们可以在图像上来看看这个点在哪里
plt.scatter(FPR[maxindex],recall[maxindex],c="black",s=30)
#把上述代码放入这段代码中:
plt.figure()
plt.plot(FPR, recall, color='red',
label='ROC curve (area = %0.2f)' % area)
plt.plot([0, 1], [0, 1], color='black', linestyle='--')
plt.scatter(FPR[maxindex],recall[maxindex],c="black",s=30)
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('Recall')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()
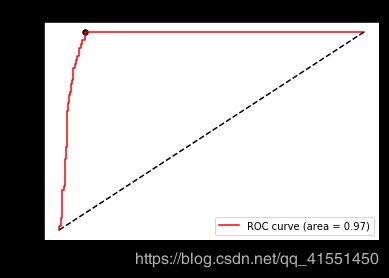
最佳阈值就这样选取出来了,由于现在我们是使用decision_function来画ROC曲线,所以我们选择出来的最佳阈值其实是最佳距离。如果我们使用的是概率,我们选取的最佳阈值就会使一个概率值了。只要我们让这个距离/概率
以上的点,都为正类,让这个距离/概率以下的点都为负类,模型就是最好的:即能够捕捉出少数类,又能够尽量不误伤多数类,整体的精确性和对少数类的捕捉都得到了保证。
而从找出的最优阈值点来看,这个点,其实是图像上离左上角最近的点,离中间的虚线最远的点,也是ROC曲线的转折点。如果没有时间进行计算,或者横坐标比较清晰的时候,我们就可以观察转折点来找到我们的最佳阈值。
到这里为止,SVC的模型评估指标就介绍完毕了。但是,SVC的样本不均衡问题还可以有很多的探索。另外,我们还可以使用KS曲线,或者收益曲线(profit chart)来选择我们的阈值,都是和ROC曲线类似的用法。大家若有余力,可以自己深入研究一下。模型评估指标,还有很多深奥的地方
3 使用SVC时的其他考虑
3.1 SVC处理多分类问题:重要参数decision_function_shape
之前所有的SVM内容,全部是基于二分类的情况来说明的,因为支持向量机是天生二分类的模型。不过,它也可以做多分类,但是SVC在多分类情况上的推广,属于恶魔级别的难度,要从数学角度去理解几乎是不可能的,因为要
研究透彻多分类状况下的SVC,就必须研究透彻多分类时所需要的决策边界个数,每个决策边界所需要的支持向量的个数,以及这些支持向量如何组合起来计算我们的拉格朗日乘数,要求我们必须对SMO或者梯度下降求解SVC的
拉格朗日乘数的过程十分熟悉。这些内容推广到多分类之后,即便在线性可分的二维数据上都已经复杂,要再推广到非线性可分的高维情况,就远远超出了我们这个课程的要求。
sklearn中用了许多巧妙的方法来为我们呈现结果,在这里,这一小节会为大家简单介绍sklearn当中是如何SVC的多分类问题的,但需要注意,这一节的内容只是一个简介,并不能带大家深入理解多分类中各种深奥的情况。大家
可根据自己的需求酌情选读。
支持向量机是天在生二分类的模型,所以支持向量机在处理多分类问题的时候,是把多分类问题转换成了二分类问题来解决。这种转换有两种模式,一种叫做“一对一”模式(one vs one),一种叫做“一对多”模式(one vs rest)。
在ovo模式下,标签中的所有类别会被两两组合,每两个类别之间建一个SVC模型,每个模型生成一个决策边界,分别进行二分类。这种模式下,对于含有n_class个标签类别的数据来说,SVC会生成总共 C n − c l a s s 2 C^2_{n-class} Cn−class2个模型,即会生成总共 C n − c l a s s 2 C^2_{n-class} Cn−class2个超平面,其中:
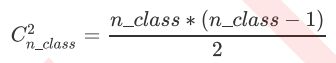
比如说,来看ovo模式下,二维空间中的三分类情况。
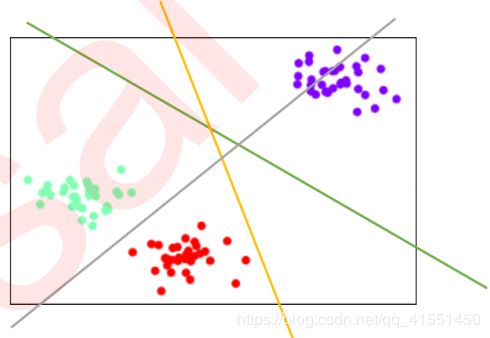
首先让提出紫色点和红色点作为一组,然后求解出两个类之间的SVC和绿色决策边界。然后让绿色点和红色点作为一组,求解出两个类之间的SVC和灰色边界。最后让绿色和紫色组成一组,组成两个类之间的SVC和黄色边界。然后基于三个边界,分别对三个类别进行分类。
在ovr模式下,标签中所有的类别会分别与其他类别进行组合,建立n_class个模型,每个模型生成一个决策边界,分别进行二分类。同样的数据集,如果是ovr模式,则会生成如下的决策边界:
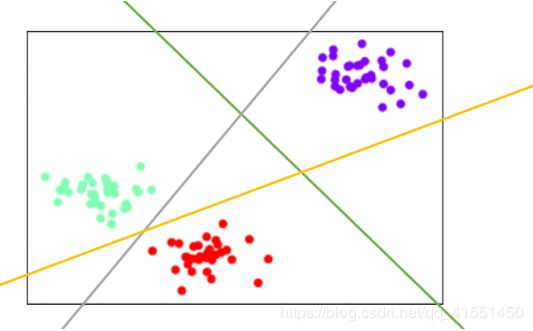
紫色类 vs 剩下的类,生成绿色的决策边界。红色类 vs 剩下的类,生成黄色的决策边界。绿色类 vs 剩下的类,生成灰色的决策边界,当类别更多的时候,如此类推下去,我们永远需要n_class个模型。
当类别更多的时候,无论是ovr还是ovo模式需要的决策边界都会越来越多,模型也会越来越复杂,不过ovo模式下的模型计算会更加复杂,因为ovo模式中的决策边界数量增加更快,但相对的,ovo模型也会更加精确。ovr模型计算更快,但是效果往往不是很好。在硬件可以支持的情况下,还是建议选择ovo模式。
一旦模型和超平面的数量变化了,SVC的很多计算过程,还有接口和属性都会发生变化:
- 在二分类中,所有的支持向量都服务于唯一的超平面,在多分类问题中,每个支持向量都会被用来服务于多个个超平面
- 在生成一个超平面的二分类过程中,我们计算一个超平面上的支持向量对应的拉格朗日乘数 ,现在,由于有多个超平面,所以需要的支持向量的个数增长了,因而求解拉格朗日乘数的需求也变得更多。在二分类问题中,每一个支持向量求解出一个拉格朗日乘数,因此拉格朗日乘数的数目和支持向量的数一致。但在多分类问题中,两个不同超平面的支持向量被用来决定一个拉格朗日乘数的取值,并且规定一个支持向量至少要被两个超平面使用。假设一个多分类问题中分别有三个超平面,超平面A上有3个支持向量,超平面B和C上分别有2个支持向量,则总共7个支持向量就需要求解14个对应的拉格朗日乘数。以这样的考虑来看,拉格朗日乘数的计算也会变得异常复杂。
- 在简单二分类中,decision_function只返回每个样本点到唯一的超平面的距离,而在多分类问题中这个接口将根据选择的多分类模式不同而返回不同的结构。
- 同理,在二分类中只生成一条直线,所以属性coef_和intercept_返回的结构都很单纯,但在多分类问题,尤其是ovo类型下,两个属性都受到不同程度的影响。
参数decision_function_shape决定我们究竟使用哪一种分类模式。
decision_function_shape
可输入“ovo",“ovr”,默认”ovr",对所有分类器,选择使用ovo或者ovr模式。
选择ovr模式,则返回的decision_function结构为(n_samples,n_class)。二分类时,尽管选用ovr模式,却会返回(n_samples,)的结构。
3.2 SVM的模型复杂度
3.3 SVM中的随机性:参数random_state
虽然不常用,但是SVC中包含参数random_state,这个参数受到probability参数的影响,仅在生辰高概率估计的时候才会生效。在概率估计中,SVC使用随机数生成器来混合数据。如果概率设置为False,则random_state对结果没有影响。如果不实现概率估计,SVM中不存在有随机性的过程。
3.4 SVC的重要属性补充
到目前为止,SVC的几乎所有重要参数,属性和接口我们都已经介绍完毕了。在这里,给大家做一个查缺补漏:
#属性n_support_:调用每个类别下的支持向量的数目
clf_proba.n_support_
#属性coef_:每个特征的重要性,这个系数仅仅适合于线性核
clf_proba.coef_
#属性intercept_:查看生成的决策边界的截距
clf_proba.intercept_
#属性dual_coef_:查看生成的拉格朗日乘数
clf_proba.dual_coef_
clf_proba.dual_coef_.shape
#注意到这个属性的结构了吗?来看看查看支持向量的属性
clf_proba.support_vectors_
clf_proba.support_vectors_.shape
#注意到dual_coef_中生成的拉格朗日乘数的数目和我们的支持向量的数目一致
#注意到KKT条件的条件中的第五条,所有非支持向量会让拉格朗日乘数为0
#所以拉格朗日乘数的数目和支持向量的数目是一致的
#注意,此情况仅仅在二分类中适用!
3.5 一窥线性支持向量机类LinearSVC
到这里,我们基本上已经了解完毕了SVC在sklearn中的使用状况。当然,还有很多可以深入的东西,大家如果感兴趣可以自己深入研究。除了最常见的SVC类之外,还有一个重要的类可以使用:线性支持向量机linearSVC。
class
sklearn.svm.LinearSVC(penalty=’l2’, loss=’squared_hinge’,
dual=True, tol=0.0001, C=1.0, multi_class=’ovr’, fit_intercept=True,
intercept_scaling=1, class_weight=None, verbose=0, random_state=None,
max_iter=1000)
线性支持向量机其实与SVC类中选择"linear"作为核函数的功能类似,但是其背后的实现库是liblinear而不是libsvm,这使得在线性数据上,linearSVC的运行速度比SVC中的“linear”核函数要快,不过两者的运行结果相似。在现实中,许多数据都是线性的,因此我们可以依赖计算得更快得LinearSVC类。除此之外,线性支持向量可以很容易地推广到大样本上,还可以支持稀疏矩阵,多分类中也支持ovr方案。
线性支持向量机的许多参数看起来和逻辑回归非常类似,比如可以选择惩罚项,可以选择损失函数等等,这让它在线性数据上表现更加灵活。
| 参数 | 含义 |
|---|---|
| penalty | 在求解决策边界过程中使用的正则惩罚项,可以输入"l1"或者"l2",默认"l2"和逻辑回归中地正则惩罚项非常类似,"l1"会让决策边界中部分特征的系数w被压缩到0,而"l2"会让每个特征都被分配到一个不为0的系数 |
| loss | 在求解决策边界过程中使用的损失函数,可以输入"hinge"或者“squared_hinge”,默认为“square_hinge”;当输入“hinge",表示默认使用和类SVC中一致的损失函数,使用”squared_hinge“表示使用SVC中损失函数的平方作为损失函数。 |
| dual | 布尔值,默认为True;选择让算法直接求解原始的拉格朗日函数,或者求解对偶函数。当选择为True的时候,表示求解对偶函数,如果样本量大于特征数目,建议求解原始拉格朗日函数,设定dual = False。 |
和SVC一样,LinearSVC也有C这个惩罚参数,但LinearSVC在C变大时对C不太敏感,并且在某个阈值之后就不能再改善结果了。同时,较大的C值将需要更多的时间进行训练,2008年时有人做过实验,LinearSVC在C很大的时候训练时间可以比原来长10倍。
4 SVC真实数据案例:预测明天是否会下雨
SVC在现实中的应用十分广泛,尤其实在图像和文字识别方面。然而,这些数据不仅非常难以获取,还难以在课程中完整呈现出来,但SVC真实应用的代码其实就是sklearn中的三行,真正能够展现出SVM强大之处的,反而很少是案例本身,而是我们之前所作的各种探索。
我们在学习算法的时候,会使用各种各样的数据集来进行演示,但这些数据往往非常干净并且规整,不需要做太多的数据预处理。在我们讲解第三章:数据预处理与特征工程时,用了自制的文字数据和kaggle上的高维数据来为大家讲解,然而这些数据依然不能够和现实中采集到的数据的复杂程度相比。因此大家学习了这门课程,却依然会对究竟怎样做预处理感到困惑。
在实际工作中,数据预处理往往比建模难得多,耗时多得多,因此合理的数据预处理是非常必要的。考虑到大家渴望学习真实数据上的预处理的需求,以及SVM需要在比较规则的数据集上来表现的特性,我为大家准备了这个Kaggle上下载的,未经过预处理的澳大利亚天气数据集。我们的目标是在这个数据集上来预测明天是否会下雨。
这个案例的核心目的,是通过巧妙的预处理和特征工程来向大家展示,在现实数据集上我们往往如何做数据预处理,或者我们都有哪些预处理的方式和思路。预测天气是一个非常非常困难的主题,因为影响天气的因素太多,而Kaggle的这份数据也丝毫不让我们失望,是一份非常难的数据集,难到我们目前学过的所有算法在这个数据集上都不会有太好的结果,尤其是召回率recall,异常地低。在这里,我为大家抛砖引玉,在这个15W行数据的数据集上,随机抽样5000个样本来为大家演示我的数据预处理和特征工程的过程,为大家提供一些数据预处理和特征工程的思路。不过,特征工程没有标准答案,因此大家应当多尝试,希望使用原数据集的小伙伴们可以到Kaggle下载最原始版本,或者直接从我们的课件打包下载的数据中获取:
Kaggle下载链接走这里:https://www.kaggle.com/jsphyg/weather-dataset-rattle-package
| 对于使用Kaggle原数据集的小伙伴的温馨提示: |
|---|
| 记得好好阅读Kaggle上的各种数据集说明哦~!有一些特征是不能够使用的! |
那就让我们开始我们的案例吧。
4.1 导库导数据,探索特征
导入需要的库
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
导入数据,探索数据
weather = pd.read_csv(r"C:\work\learnbetter\micro-class\week 8 SVM (2)\data\weatherAUS5000.csv",index_col=0)
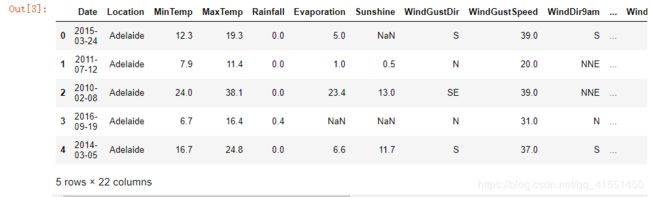
weather.head()
| 特征/标签 | 含义 |
|---|---|
| Date | 观察日期 |
| Location | 获取该信息的气象站的名称 |
| MinTemp | 以摄氏度为单位的最低温度 |
| MaxTemp | 以摄氏度为单位的最高温度 |
| Rainfall | 当天记录的降雨量,单位为mm |
| Evaporation | 到早上9点之前的24小时的A级蒸发量(mm) |
| Sunshine | 白日受到日照的完整小时 |
| WindGustDir | 在到午夜12点前的24小时中的最强风的风向 |
| WindGustSpeed | 在到午夜12点前的24小时中的最强风速(km / h) |
| WindDir9am | 上午9点时的风向 |
| WindDir3pm | 下午3点时的风向 |
| WindSpeed9am | 上午9点之前每个十分钟的风速的平均值(km / h) |
| WindSpeed3pm | 下午3点之前每个十分钟的风速的平均值(km / h) |
| Humidity9am | 上午9点的湿度(百分比) |
| Humidity3am | 下午3点的湿度(百分比) |
| Pressure9am | 上午9点平均海平面上的大气压(hpa) |
| Pressure3pm | 下午3点平均海平面上的大气压(hpa) |
| Cloud9am | 上午9点的天空被云层遮蔽的程度,这是以“oktas”来衡量的,这个单位记录了云层遮挡天空的程度。0表示完全晴朗的天空,而8表示它完全是阴天。 |
| Cloud3pm | 下午3点的天空被云层遮蔽的程度 |
| Temp9am | 上午9点的摄氏度温度 |
| Temp3pm | 下午3点的摄氏度温度 |
| RainTomorrow | 目标变量,我们的标签:明天下雨了吗? |
#将特征矩阵和标签Y分开
X = weather.iloc[:,:-1]
Y = weather.iloc[:,-1]
#分裂的快捷键:ctrl shift -
#合并的快捷键:shift M
X.shape #5000行是我随机选的
#探索数据类型
X.info()
#探索缺失值
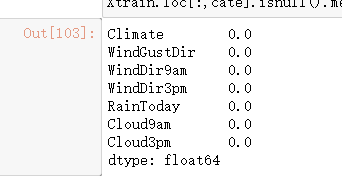
X.isnull().mean() #缺失值所占总值的比例 isnull().sum(全部的True)/X.shape[0]
#我们要有不同的缺失值填补策略
#探索标签的分类
np.unique(Y) #我们的标签是二分类
粗略观察可以发现,这个特征矩阵由一部分分类变量和一部分连续变量组成,其中云层遮蔽程度虽然是以数字表示,但是本质却是分类变量。大多数特征都是采集的自然数据,比如蒸发量,日照时间,湿度等等,而少部分特征是人为构成的。还有一些是单纯表示样本信息的变量,比如采集信息的地点,以及采集的时间。
4.2 分集,优先探索标签
分训练集和测试集,并做描述性统计
#分训练集和测试集
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,Y,test_size=0.3,random_state=420) #随机抽样
#恢复索引
for i in [Xtrain, Xtest, Ytrain, Ytest]:
i.index = range(i.shape[0])
在现实中,我们会先分训练集和测试集,再开始进行数据预处理。这是由于,测试集在现实中往往是不可获得的,或者被假设为是不可获得的,我们不希望我们建模的任何过程受到测试集数据的影响,否则的话,就相当于提前告诉了模型一部分预测的答案。在之前的课中,为了简便操作,都给大家忽略了这个过程,一律先进行预处理,再分训练集和测试集,这是一种不规范的做法。在这里,为了让案例尽量接近真实的样貌,所以采取了现实中所使用的这种方式:先分训练集和测试集,再一步步进行预处理。这样导致的结果是,我们对训练集执行的所有操作,都必须对测试集执行一次,工作量是翻倍的。
#是否有样本不平衡问题?
Ytrain.value_counts()
Ytest.value_counts()
#将标签编码
from sklearn.preprocessing import LabelEncoder #标签专用,第三章讲过
encorder = LabelEncoder().fit(Ytrain) #允许一维数据的输入的
#认得了:有两类,YES和NO,YES是1,NO是0
#使用训练集进行训练,然后在训练集和测试集上分别进行transform
Ytrain = pd.DataFrame(encorder.transform(Ytrain))
Ytest = pd.DataFrame(encorder.transform(Ytest))
#如果我们的测试集中,出现了训练集中没有出现过的标签类别
#比如说,测试集中有YES, NO, UNKNOWN
#而我们的训练集中只有YES和NO
4.3 探索特征,开始处理特征矩阵
4.3.1 描述性统计与异常值
#描述性统计
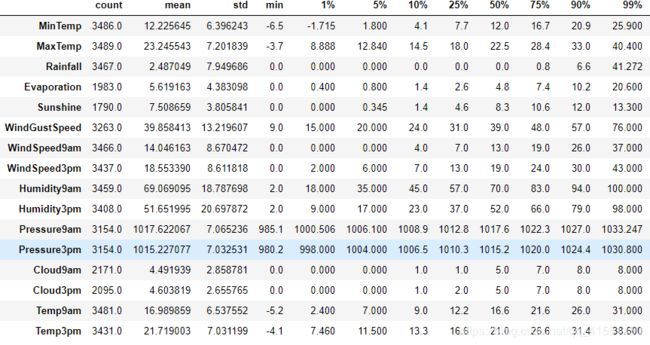
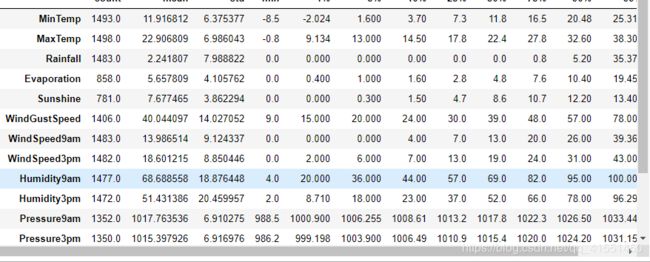
Xtrain.describe([0.01,0.05,0.1,0.25,0.5,0.75,0.9,0.99]).T
Xtest.describe([0.01,0.05,0.1,0.25,0.5,0.75,0.9,0.99]).T
#对于去kaggle上下载了数据的小伙伴们,以及对于坚持要使用完整版数据的(15W行)数据的小伙伴们
#如果你发现了异常值,首先你要观察,这个异常值出现的频率
#如果异常值只出现了一次,多半是输入错误,直接把异常值删除
#如果异常值出现了多次,去跟业务人员沟通,人为造成的错误异常值留着是没有用的
#如果异常值占到你总数据量的10%左右了 - 把异常值替换成非异常但是非干扰的项,比如说用0来进行替换,或者把异常当缺失
#先查看原始的数据结构
Xtrain.shape
Xtest.shape
#观察异常值是大量存在,还是少数存在
Xtrain.loc[Xtrain.loc[:,"Cloud9am"] == 9,"Cloud9am"]
Xtest.loc[Xtest.loc[:,"Cloud9am"] == 9,"Cloud9am"]
Xtest.loc[Xtest.loc[:,"Cloud3pm"] == 9,"Cloud3pm"]
#少数存在,于是采取删除的策略
#注意如果删除特征矩阵,则必须连对应的标签一起删除,特征矩阵的行和标签的行必须要一一对应
Xtrain = Xtrain.drop(index = 71737)
Ytrain = Ytrain.drop(index = 71737)
#删除完毕之后,观察原始的数据结构,确认删除正确
Xtrain.shape
Xtest = Xtest.drop(index = [19646,29632])
Ytest = Ytest.drop(index = [19646,29632])
Xtest.shape
#进行任何行删除之后,千万记得要恢复索引
for i in [Xtrain, Xtest, Ytrain, Ytest]:
i.index = range(i.shape[0])
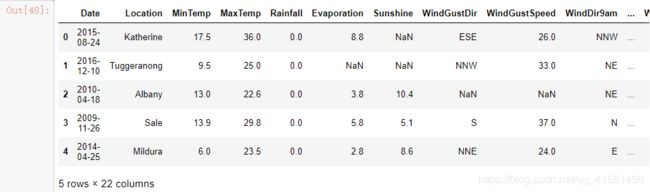
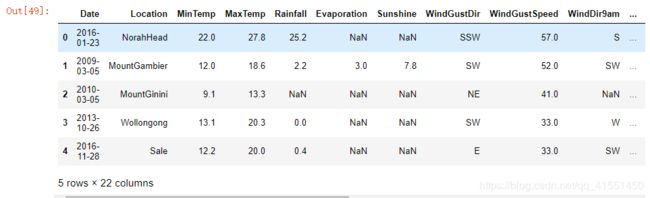
Xtrain.head()
Xtest.head()
4.3.2 处理困难特征:日期
我们采集数据的日期是否和我们的天气有关系呢?我们可以探索一下我们的采集日期有什么样的性质:
Xtrainc = Xtrain.copy()
Xtrainc.sort_values(by="Location")
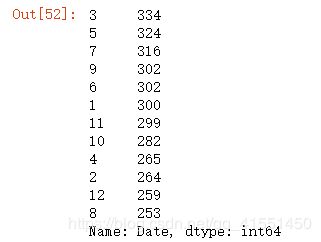
Xtrain.iloc[:,0].value_counts()
#首先,日期不是独一无二的,日期有重复
#其次,在我们分训练集和测试集之后,日期也不是连续的,而是分散的
#某一年的某一天倾向于会下雨?或者倾向于不会下雨吗?
#不是日期影响了下雨与否,反而更多的是这一天的日照时间,湿度,温度等等这些因素影响了是否会下雨
#光看日期,其实感觉它对我们的判断并无直接影响
#如果我们把它当作连续型变量处理,那算法会人为它是一系列1~3000左右的数字,不会意识到这是日期
Xtrain.iloc[:,0].value_counts().count()
#如果我们把它当作分类型变量处理,类别太多,有2141类,如果换成数值型,会被直接当成连续型变量,如果做成哑变量,我们特征的维度会爆炸
如果我们的思考简单一些,我们可以直接删除日期这个特征。首先它不是一个直接影响我们标签的特征,并且要处理日期其实是非常困难的。如果大家认可这种思路,那可以直接运行下面的代码来删除我们的日期:
Xtrain = Xtrain.drop(["Date"],axis=1)
Xtest = Xtest.drop(["Date"],axis=1)
但在这里,很多人可能会持不同意见,怎么能够随便删除一个特征(哪怕我们已经觉得它可能无关)?如果我们要删除,我们可能需要一些统计过程,来判断说这个特征确实是和标签无关的,那我们可以先将“日期”这个特征编码后对它和标签做方差齐性检验(ANOVA),如果检验结果表示日期这个特征的确和我们的标签无关,那我们就可以愉快地删除这个特征了。但要编码“日期”这个特征,就又回到了它到底是否会被算法当成是分类变量的问题上。
其实我们可以想到,日期必然是和我们的结果有关的,它会从两个角度来影响我们的标签:
首先,我们可以想到,昨天的天气可能会影响今天的天气,而今天的天气又可能会影响明天的天气。也就是说,随着日期的逐渐改变,样本是会受到上一个样本的影响的。但是对于算法来说,普通的算法是无法捕捉到样本与样本之间的联系的,我们的算法捕捉的是样本的每个特征与标签之间的联系(即列与列之间的联系),而无法捕捉样本与样本之间的联系(行与行的联系)。
要让算法理解上一个样本的标签可能会影响下一个样本的标签,我们必须使用时间序列分析。时间序列分析是指将同一统计指标的数值按其发生的时间先后顺序排列而成的数列。时间序列分析的主要目的是根据已有的历史数据对未来进行预测。然而,(据我所知)时间序列只能在单调的,唯一的时间上运行,即一次只能够对一个地点进行预测,不能够实现一次性预测多个地点,除非进行循环。而我们的时间数据本身,不是单调的,也不是唯一的,经过抽样之后,甚至连连续的都不是了,我们的时间是每个混杂在多个地点中,每个地点上的一小段时间。如何使用时间序列来处理这个问题,就会变得复杂。
那我们可以换一种思路,既然算法处理的是列与列之间的关系,我是否可以把”今天的天气会影响明天的天气“这个指标转换成一个特征呢?我们就这样来操作。
我们观察到,我们的特征中有一列叫做“Rainfall",这是表示当前日期当前地区下的降雨量,换句话说,也就是”今天的降雨量“。凭常识我们认为,今天是否下雨,应该会影响明天是否下雨,比如有的地方可能就有这样的气候,一旦下雨就连着下很多天,也有可能有的地方的气候就是一场暴雨来得快去的快。因此,我们可以将时间对气候的连续影响,转换为”今天是否下雨“这个特征,巧妙地将样本对应标签之间的联系,转换成是特征与标签之间的联系了。
Xtrain["Rainfall"].head(20)
Xtrain.loc[Xtrain["Rainfall"] >= 1,"RainToday"] = "Yes"
Xtrain.loc[Xtrain["Rainfall"] < 1,"RainToday"] = "No"
Xtrain.loc[Xtrain["Rainfall"] == np.nan,"RainToday"] = np.nan
Xtest.loc[Xtest["Rainfall"] >= 1,"RainToday"] = "Yes"
Xtest.loc[Xtest["Rainfall"] < 1,"RainToday"] = "No"
Xtest.loc[Xtest["Rainfall"] == np.nan,"RainToday"] = np.nan
Xtrain.head()
Xtest.head()
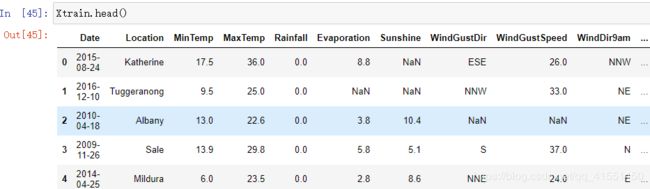
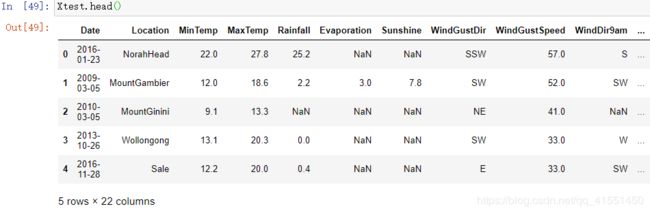
如此,我们就创造了一个特征,今天是否下雨“RainToday”。
那现在,我们是否就可以将日期删除了呢?对于我们而言,日期本身并不影响天气,但是日期所在的月份和季节其实是影响天气的,如果任选梅雨季节的某一天,那明天下雨的可能性必然比非梅雨季节的那一天要大。虽然我们无法让机器学习体会不同月份是什么季节,但是我们可以对不同月份进行分组,算法可以通过训练感受到,“这个月或者这个季节更容易下雨”。因此,我们可以将月份或者季节提取出来,作为一个特征使用,而舍弃掉具体的日期。如此,我们又可以创造第二个特征,月份"Month"。
int(Xtrain.loc[0,"Date"].split("-")[1]) #提取出月份
Xtrain["Date"] = Xtrain["Date"].apply(lambda x:int(x.split("-")[1]))
#apply是对dataframe上的某一列进行处理的一个函数
#lambda x匿名函数,请在dataframe上这一列中的每一行帮我执行冒号后的命令
Xtrain.loc[:,"Date"].value_counts()
#替换完毕后,我们需要修改列的名称
#rename是比较少用的,可以用来修改单个列名的函数
#我们通常都直接使用 df.columns = 某个列表 这样的形式来一次修改所有的列名
#但rename允许我们只修改某个单独的列
Xtrain = Xtrain.rename(columns={"Date":"Month"})
Xtest["Date"] = Xtest["Date"].apply(lambda x:int(x.split("-")[1]))
Xtest = Xtest.rename(columns={"Date":"Month"})
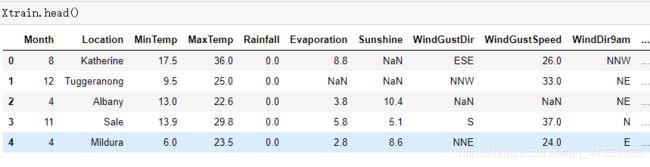

通过时间,我们处理出两个新特征,“今天是否下雨”和“月份”。接下来,让我们来看看如何处理另一个更加困难的特征,地点。
4.3.3 处理困难特征:地点
地点,又是一个非常tricky的特征。常识上来说,我们认为地点肯定是对明天是否会下雨存在影响的。比如说,如果其他信息都不给出,我们只猜测,“伦敦明天是否会下雨”和”北京明天是否会下雨“,我一定会猜测伦敦会下雨,而北京不会,因为伦敦是常年下雨的城市,而北京的气候非常干燥。对澳大利亚这样面积巨大的国家来说,必然存在着不同的城市有着不同的下雨倾向的情况。但尴尬的是,和时间一样,我们输入地点的名字对于算法来说,就是一串字符,"London"和"Beijing"对算法来说,和0,1没有区别。同样,我们的样本中含有49个不同地点,如果做成分类型变量,算法就无法辨别它究竟是否是分类变量。也就是说,我们需要让算法意识到,不同的地点因为气候不同,所以对“明天是否会下雨”有着不同的影响。如果我们能够将地点转换为这个地方的气候的话,我们就可以将不同城市打包到同一个气候中,而同一个气候下反应的降雨情况应该是相似的。
那我们如何将城市转换为气候呢?我在google找到了如下地图:
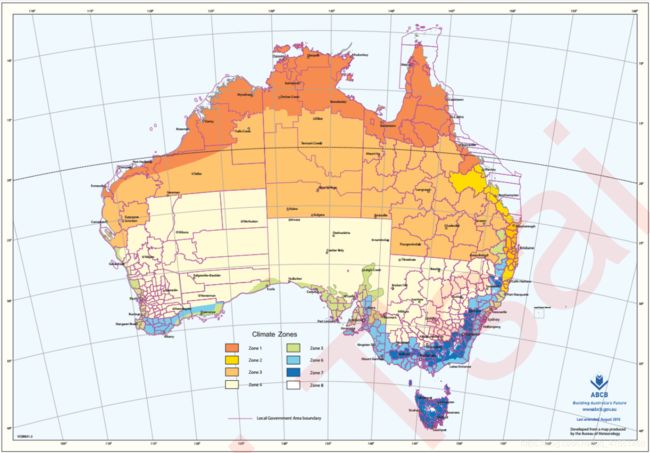
这是由澳大利亚气象局和澳大利亚建筑规范委员会(ABCB)制作统计的,澳大利亚不同地区不同城市的所在的气候区域划分。总共划分为八个区域,非常适合我们用来做分类。如果能够把49个地点转换成八种不同的气候,这个信息应该会对是否下雨的判断比较有用。基于气象局和ABCB的数据,我为大家制作了澳大利亚主要城市所对应的气候类型数据,并保存在csv文件city_climate.csv当中。然后,我使用以下代码,在google上进行爬虫,爬出了每个城市所对应的经纬度,并保存在数据cityll.csv当中,大家可以自行导入,来查看这个数据。
爬虫的过程,我录制成了短视频,详细的解释和操作大家可以在视频里看到:
https://www.bilibili.com/video/av39338080/
爬虫的代码如下所示,大家可以把谷歌的主页换成百度,修改一下爬虫的命令,就可以自己试试看这段代码。注意要先定义你需要爬取的城市名称的列表cityname哦。
import time
from selenium import webdriver #导入需要的模块,其中爬虫使用的是selenium
import pandas as pd
import numpy as np
df = pd.DataFrame(index=range(len(cityname))) #创建新dataframe用于存储爬取的数据
driver = webdriver.Chrome() #调用谷歌浏览器
time0 = time.time() #计时开始
#循环开始
for num, city in enumerate(cityname): #在城市名称中进行遍历
driver.get('https://www.google.co.uk/webhp?
hl=en&sa=X&ved=0ahUKEwimtcX24cTfAhUJE7wKHVkWB5AQPAgH')
#首先打开谷歌主页
time.sleep(0.3)
#停留0.3秒让我们知道发生了什么
search_box = driver.find_element_by_name('q') #锁定谷歌的搜索输入框
search_box.send_keys('%s Australia Latitude and longitude' % (city)) #在输入框中输入“城市” 澳大利亚 经纬度
search_box.submit() #enter,确认开始搜索
result = driver.find_element_by_xpath('//div[@class="Z0LcW"]').text #?爬取需要的经纬度,就是这里,怎么获取的呢?
resultsplit = result.split(" ") #将爬取的结果用split进行分割
df.loc[num,"City"] = city #向提前创建好的df中输入爬取的数据,第一列是城市名
df.loc[num,"Latitude"] = resultsplit[0] #第二列是纬度
df.loc[num,"Longitude"] = resultsplit[2] #第三列是经度
df.loc[num,"Latitudedir"] = resultsplit[1] #第四列是纬度的方向
df.loc[num,"Longitudedir"] = resultsplit[3] #第五列是经度的方向
print("%i webcrawler successful for city %s" % (num,city)) #每次爬虫成功之后,就打印“城市”成功了
time.sleep(1) #全部爬取完毕后,停留1秒钟
driver.quit() #关闭浏览器
print(time.time() - time0) #打印所需的时间
为什么我们会需要城市的经纬度呢?我曾经尝试过直接使用样本中的城市来爬取城市本身的气候,然而由于样本中的地点名称,其实是气候站的名称,而不是城市本身的名称,因此不是每一个城市都能够直接获取到城市的气候。
比如说,如果我们搜索“海淀区气候”,搜索引擎返回的可能是海淀区现在的气温,而不是整个北京的气候类型。因此,我们需要澳大利亚气象局的数据,来找到这些气候站所对应的城市。
我们有了澳大利亚全国主要城市的气候,也有了澳大利亚主要城市的经纬度(地点),我们就可以通过计算我们样本中的每个气候站到各个主要城市的地理距离,来找出一个离这个气象站最近的主要城市,而这个主要城市的气候就是我们样本点所在的地点的气候。
让我们把cityll.csv和cityclimate.csv来导入,来看看它们是什么样子:
cityll = pd.read_csv(r"C:\work\learnbetter\micro-class\week 8 SVM (2)\cityll.csv",index_col=0)
city_climate = pd.read_csv(r"C:\work\learnbetter\micro-class\week 8 SVM (2)\Cityclimate.csv")
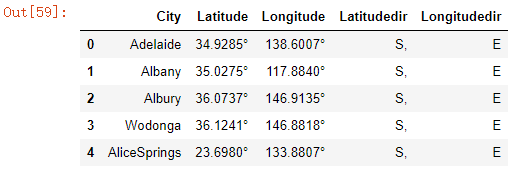
cityll.head() #每个城市对应的经纬度,这些城市是澳大利亚统计局做的那张地图上的城市
float(cityll.loc[0,"Latitude"][:-1])
#34.9285
cityll.loc[:,"Latitudedir"].value_counts()
#S, 100
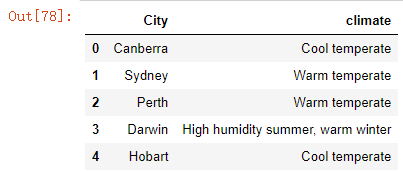
city_climate.head() #澳大利亚统计局做的每个城市对应的气候
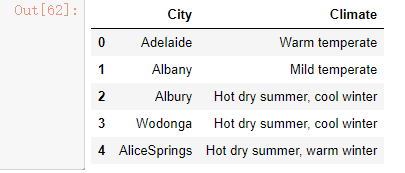
接下来,我们来将这两张表处理成可以使用的样子,首先要去掉cityll中经纬度上带有的度数符号,然后要将两张表合并起来。
#去掉度数符号
cityll["Latitudenum"] = cityll["Latitude"].apply(lambda x:float(x[:-1]))
cityll["Longitudenum"] = cityll["Longitude"].apply(lambda x:float(x[:-1]))
#观察一下所有的经纬度方向都是一致的,全部是南纬,东经,因为澳大利亚在南半球,东半球
#所以经纬度的方向我们可以舍弃了
citylld = cityll.iloc[:,[0,5,6]]
#将city_climate中的气候添加到我们的citylld中
citylld["climate"] = city_climate.iloc[:,-1]
citylld.head()
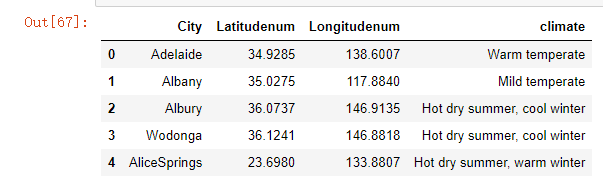
接下来,我们如果想要计算距离,我们就会需要所有样本数据中的城市。我们认为,只有出现在训练集中的地点才会出现在测试集中,基于这样的假设,我们来爬取训练集中所有的地点所对应的经纬度,并且保存在一个csv文件samplecity.csv中:
#训练集中所有的地点
cityname = Xtrain.iloc[:,1].value_counts().index.tolist()
cityname
import time
from selenium import webdriver #导入需要的模块,其中爬虫使用的是selenium
import pandas as pd
import numpy as np
df = pd.DataFrame(index=range(len(cityname))) #创建新dataframe用于存储爬取的数据
driver = webdriver.Chrome() #调用谷歌浏览器
time0 = time.time() #计时开始
#循环开始
for num, city in enumerate(cityname): #在城市名称中进行遍历
driver.get('https://www.google.co.uk/webhp?
hl=en&sa=X&ved=0ahUKEwimtcX24cTfAhUJE7wKHVkWB5AQPAgH')
#首先打开谷歌主页
time.sleep(0.3)
#停留0.3秒让我们知道发生了什么
search_box = driver.find_element_by_name('q') #锁定谷歌的搜索输入框
search_box.send_keys('%s Australia Latitude and longitude' % (city)) #在输入框中输入“城市” 澳大利亚 经纬度
search_box.submit() #enter,确认开始搜索
result = driver.find_element_by_xpath('//div[@class="Z0LcW"]').text #?爬取需要的经纬度,就是这里,怎么获取的呢?
resultsplit = result.split(" ") #将爬取的结果用split进行分割
df.loc[num,"City"] = city #向提前创建好的df中输入爬取的数据,第一列是城市名
df.loc[num,"Latitude"] = resultsplit[0] #第二列是经度
df.loc[num,"Longitude"] = resultsplit[2] #第三列是纬度
df.loc[num,"Latitudedir"] = resultsplit[1] #第四列是经度的方向
df.loc[num,"Longitudedir"] = resultsplit[3] #第五列是纬度的方向
print("%i webcrawler successful for city %s" % (num,city)) #每次爬虫成功之后,就打印“城市”成功了
time.sleep(1) #全部爬取完毕后,停留1秒钟
driver.quit() #关闭浏览器
print(time.time() - time0) #打印所需的时间
df.to_csv(r"C:\work\learnbetter\micro-class\week 8 SVM (2)\samplecity.csv")
来查看一下我们爬取出的内容是什么样子:
samplecity = pd.read_csv(r"C:\work\learnbetter\micro-class\week 8 SVM
(2)\samplecity.csv",index_col=0)
#我们对samplecity也执行同样的处理:去掉经纬度中度数的符号,并且舍弃我们的经纬度的方向
samplecity["Latitudenum"] = samplecity["Latitude"].apply(lambda x:float(x[:-1]))
samplecity["Longitudenum"] = samplecity["Longitude"].apply(lambda x:float(x[:-1]))
samplecityd = samplecity.iloc[:,[0,5,6]]
samplecityd.head()
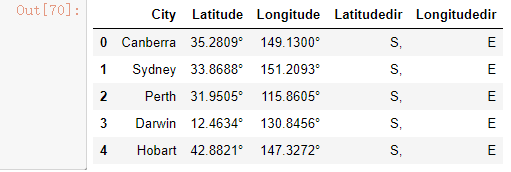
好了,我们现在有了澳大利亚主要城市的经纬度和对应的气候,也有了我们的样本的地点所对应的经纬度,接下来我们要开始计算我们样本上的地点到每个澳大利亚主要城市的距离,而离我们的样本地点最近的那个澳大利亚主要城市的气候,就是我们样本点的气候。在地理上,两个地点之间的距离,由如下公式来进行计算:
![]()
其中R是地球的半径,6371.01km,arccos是三角反余弦函数,slat是起始地点的纬度,slon是起始地点的经度,elat是结束地点的纬度,elon是结束地点的经度。本质还是计算两点之间的距离。而我们爬取的经纬度,本质其实是角度,所以需要用各种三角函数和弧度公式将角度转换成距离。由于我们不是地理专业,拿到公式可以使用就okay了,不需要去纠结这个公式究竟怎么来的。
#首先使用radians将角度转换成弧度
from math import radians, sin, cos, acos
citylld.loc[:,"slat"] = citylld.iloc[:,1].apply(lambda x : radians(x))
citylld.loc[:,"slon"] = citylld.iloc[:,2].apply(lambda x : radians(x))
samplecityd.loc[:,"elat"] = samplecityd.iloc[:,1].apply(lambda x : radians(x))
samplecityd.loc[:,"elon"] = samplecityd.iloc[:,2].apply(lambda x : radians(x))
import sys
for i in range(samplecityd.shape[0]):
slat = citylld.loc[:,"slat"]
slon = citylld.loc[:,"slon"]
elat = samplecityd.loc[i,"elat"]
elon = samplecityd.loc[i,"elon"]
dist = 6371.01 * np.arccos(np.sin(slat)*np.sin(elat) +
np.cos(slat)*np.cos(elat)*np.cos(slon.values - elon))
city_index = np.argsort(dist)[0]
#每次计算后,取距离最近的城市,然后将最近的城市和城市对应的气候都匹配到samplecityd中
samplecityd.loc[i,"closest_city"] = citylld.loc[city_index,"City"]
samplecityd.loc[i,"climate"] = citylld.loc[city_index,"climate"]
#查看最后的结果,需要检查城市匹配是否基本正确
samplecityd.head()
#查看气候的分布
samplecityd["climate"].value_counts()
#确认无误后,取出样本城市所对应的气候,并保存
locafinal = samplecityd.iloc[:,[0,-1]]
locafinal.head()
locafinal.columns = ["Location","Climate"]
#在这里设定locafinal的索引为地点,是为了之后进行map的匹配
locafinal = locafinal.set_index(keys="Location")
locafinal.to_csv(r"C:\work\learnbetter\micro-class\week 8 SVM (2)\samplelocation.csv")
locafinal.head()
locafinal.columns = ["Location","Climate"]
#在这里设定locafinal的索引为地点,是为了之后进行map的匹配
locafinal = locafinal.set_index(keys="Location")
locafinal.to_csv(r"C:\work\learnbetter\micro-class\week 8 SVM (2)\samplelocation.csv")
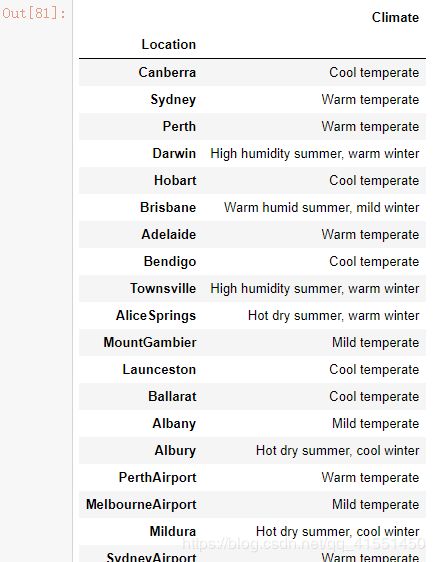
locafinal
有了每个样本城市所对应的气候,我们接下来就使用气候来替掉原本的城市,原本的气象站的名称。在这里,我们可以使用map功能,map能够将特征中的值一一对应到我们设定的字典中,并且用字典中的值来替换样本中原本的值,我们在评分卡中曾经使用这个功能来用WOE替换我们原本的特征的值。
#是否还记得训练集长什么样呢?
Xtrain.head()
#将location中的内容替换,并且确保匹配进入的气候字符串中不含有逗号,气候两边不含有空格
#我们使用re这个模块来消除逗号
#re.sub(希望替换的值,希望被替换成的值,要操作的字符串)
#x.strip()是去掉空格的函数
import re
Xtrain["Location"] = Xtrain["Location"].map(locafinal.iloc[:,0]).apply(lambda
x:re.sub(",","",x.strip()))
Xtest["Location"] = Xtest["Location"].map(locafinal.iloc[:,0]).apply(lambda
x:re.sub(",","",x.strip()))
#修改特征内容之后,我们使用新列名“Climate”来替换之前的列名“Location”
#注意这个命令一旦执行之后,就再没有列"Location"了,使用索引时要特别注意
Xtrain = Xtrain.rename(columns={"Location":"Climate"})
Xtest = Xtest.rename(columns={"Location":"Climate"})
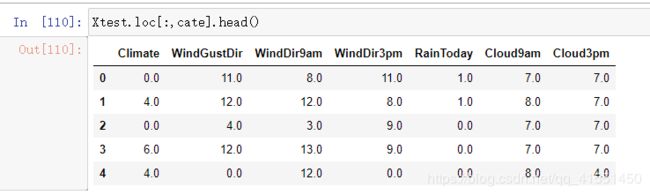
Xtrain.head()
Xtest.head()
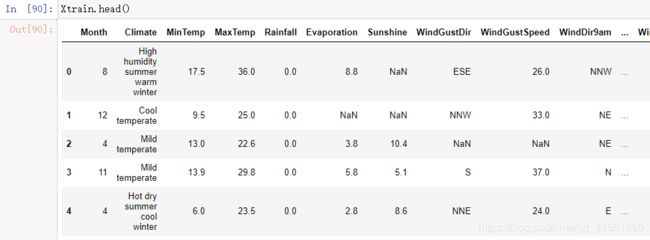
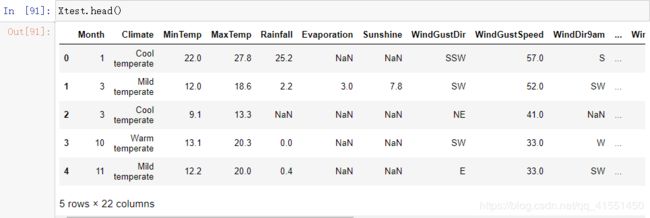
到这里,地点就处理完毕了。其实,我们还没有将这个特征转化为数字,即还没有对它进行编码。我们稍后和其他的分类型变量一起来编码。
4.3.4 处理分类型变量:缺失值
接下来,我们总算可以开始处理我们的缺失值了。首先我们要注意到,由于我们的特征矩阵由两种类型的数据组成:分类型和连续型,因此我们必须对两种数据采用不同的填补缺失值策略。传统地,如果是分类型特征,我们则采用众数进行填补。如果是连续型特征,我们则采用均值来填补。
此时,由于我们已经分了训练集和测试集,我们需要考虑一件事:究竟使用哪一部分的数据进行众数填补呢?答案是,使用训练集上的众数对训练集和测试集都进行填补。为什么会这样呢?按道理说就算用测试集上的众数对测试集进行填补,也不会使测试集数据进入我们建好的模型,不会给模型透露一些信息。然而,在现实中,我们的测试集未必是很多条数据,也许我们的测试集只有一条数据,而某个特征上是空值,此时此刻测试集本身的众数根本不存在,要如何利用测试集本身的众数去进行填补呢?因此为了避免这种尴尬的情况发生,我们假设测试集和训练集的数据分布和性质都是相似的,因此我们统一使用训练集的众数和均值来对测试集进行填补。
在sklearn当中,即便是我们的填补缺失值的类也需要由实例化,fit和接口调用执行填补三个步骤来进行,而这种分割其实一部分也是为了满足我们使用训练集的建模结果来填补测试集的需求。我们只需要实例化后,使用训练集进行fit,然后在调用接口执行填补时用训练集fit后的结果分别来填补测试集和训练集就可以了。
#查看缺失值的缺失情况
Xtrain.isnull().mean()
#首先找出,分类型特征都有哪些
cate = Xtrain.columns[Xtrain.dtypes == "object"].tolist()
#除了特征类型为"object"的特征们,还有虽然用数字表示,但是本质为分类型特征的云层遮蔽程度
cloud = ["Cloud9am","Cloud3pm"]
cate = cate + cloud
cate
#对于分类型特征,我们使用众数来进行填补
from sklearn.impute import SimpleImputer
si = SimpleImputer(missing_values=np.nan,strategy="most_frequent")
#注意,我们使用训练集数据来训练我们的填补器,本质是在生成训练集中的众数
si.fit(Xtrain.loc[:,cate])
#然后我们用训练集中的众数来同时填补训练集和测试集
Xtrain.loc[:,cate] = si.transform(Xtrain.loc[:,cate])
Xtest.loc[:,cate] = si.transform(Xtest.loc[:,cate])
Xtrain.head()
Xtest.head()
#查看分类型特征是否依然存在缺失值
Xtrain.loc[:,cate].isnull().mean()
Xtest.loc[:,cate].isnull().mean()
4.3.5 处理分类型变量:将分类型变量编码
在编码中,和我们的填补缺失值一样,我们也是需要先用训练集fit模型,本质是将训练集中已经存在的类别转换成是数字,然后我们再使用接口transform分别在测试集和训练集上来编码我们的特征矩阵。当我们使用接口在测试集上进行编码的时候,如果测试集上出现了训练集中从未出现过的类别,那代码就会报错,表示说“我没有见过这个类别,我无法对这个类别进行编码”,此时此刻你就要思考,你的测试集上或许存在异常值,错误值,或者的确有一个新的类别出现了,而你曾经的训练数据中并没有这个类别。以此为基础,你需要调整你的模型。
#将所有的分类型变量编码为数字,一个类别是一个数字
from sklearn.preprocessing import OrdinalEncoder
oe = OrdinalEncoder()
#利用训练集进行fit
oe = oe.fit(Xtrain.loc[:,cate])
#用训练集的编码结果来编码训练和测试特征矩阵
#在这里如果测试特征矩阵报错,就说明测试集中出现了训练集中从未见过的类别
Xtrain.loc[:,cate] = oe.transform(Xtrain.loc[:,cate])
Xtest.loc[:,cate] = oe.transform(Xtest.loc[:,cate])
Xtrain.loc[:,cate].head()
Xtest.loc[:,cate].head()
4.3.6 处理连续型变量:填补缺失值
连续型变量的缺失值由均值来进行填补。连续型变量往往已经是数字,无需进行编码转换。与分类型变量中一样,我们也是使用训练集上的均值对测试集进行填补。如果学过随机森林填补缺失值的小伙伴,可能此时会问,为什么不使用算法来进行填补呢?使用算法进行填补也是没有问题的,但在现实中,其实我们非常少用到算法来进行填补,有以下几个理由:
- 算法是黑箱,解释性不强。如果你是一个数据挖掘工程师,你使用算法来填补缺失值后,你不懂机器学习的老板或者同事问你的缺失值是怎么来的,你可能需要从头到尾帮他/她把随机森林解释一遍,这种效率过低的事情是不可能做的,而许多老板和上级不会接受他们无法理解的东西。
- 算法填补太过缓慢,运行一次森林需要有至少100棵树才能够基本保证森林的稳定性,而填补一个列就需要很长的时间。在我们并不知道森林的填补结果是好是坏的情况下,填补一个很大的数据集风险非常高,有可能需要跑好几个小时,但填补出来的结果却不怎么优秀,这明显是一个低效的方法。
因此在现实工作时,我们往往使用易于理解的均值或者中位数来进行填补。当然了,在算法比赛中,我们可以穷尽一切我们能够想到的办法来填补缺失值以追求让模型的效果更好,不过现实中,除了模型效果之外,我们还要追求可解释性。
col = Xtrain.columns.tolist()
for i in cate:
col.remove(i)
col
#实例化模型,填补策略为"mean"表示均值
impmean = SimpleImputer(missing_values=np.nan,strategy = "mean")
#用训练集来fit模型
impmean = impmean.fit(Xtrain.loc[:,col])
#分别在训练集和测试集上进行均值填补
Xtrain.loc[:,col] = impmean.transform(Xtrain.loc[:,col])
Xtest.loc[:,col] = impmean.transform(Xtest.loc[:,col])
Xtrain.head()
Xtest.head()
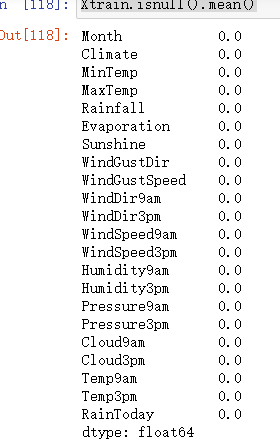
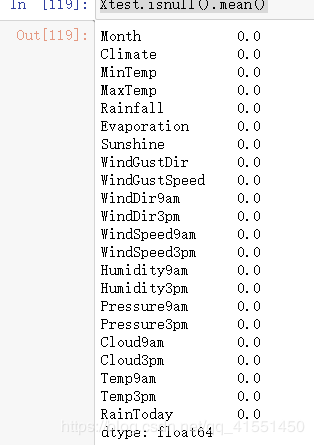
Xtrain.isnull().mean()
Xtest.isnull().mean()
4.3.7 处理连续型变量:无量纲化
数据的无量纲化是SVM执行前的重要步骤,因此我们需要对数据进行无量纲化。但注意,这个操作我们不对分类型变量进行。
col.remove("Month")
col
from sklearn.preprocessing import StandardScaler #数据转换为均值为0,方差为1的数据
#标准化不改变数据的分布,不会把数据变成正态分布的
ss = StandardScaler()
ss = ss.fit(Xtrain.loc[:,col])
Xtrain.loc[:,col] = ss.transform(Xtrain.loc[:,col])
Xtest.loc[:,col] = ss.transform(Xtest.loc[:,col])
Xtrain.head()
Xtest.head()
Ytrain.head()
Ytest.head()
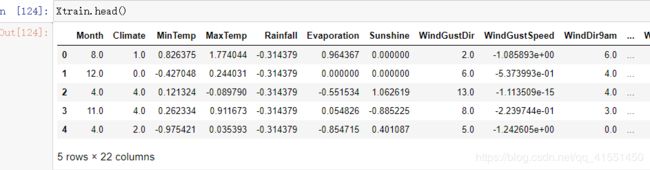

特征工程到这里就全部结束了。大家可以分别查看一下我们的Ytrain,Ytest,Xtrain,Xtest,确保我们熟悉他们的结构并且确保我们的确已经处理完毕全部的内容。将数据处理完毕之后,建议大家都使用to_csv来保存我们已经处理好的数据集,避免我们在后续建模过程中出现覆盖了原有的数据集的失误后,需要从头开始做数据预处理。在开始建模之前,无比保存好处理好的数据,然后在建模的时候,重新将数据导入。
4.4 建模与模型评估
from time import time
import datetime
from sklearn.svm import SVC
from sklearn.model_selection import cross_val_score
from sklearn.metrics import roc_auc_score, recall_score
Ytrain = Ytrain.iloc[:,0].ravel()
Ytest = Ytest.iloc[:,0].ravel()
#建模选择自然是我们的支持向量机SVC,首先用核函数的学习曲线来选择核函数
#我们希望同时观察,精确性,recall以及AUC分数
times = time() #因为SVM是计算量很大的模型,所以我们需要时刻监控我们的模型运行时间
for kernel in ["linear","poly","rbf","sigmoid"]:
clf = SVC(kernel = kernel
,gamma="auto"
,degree = 1
,cache_size = 5000
).fit(Xtrain, Ytrain)
result = clf.predict(Xtest)
score = clf.score(Xtest,Ytest)
recall = recall_score(Ytest, result)
auc = roc_auc_score(Ytest,clf.decision_function(Xtest))
print("%s 's testing accuracy %f, recall is %f', auc is %f" %
(kernel,score,recall,auc))
print(datetime.datetime.fromtimestamp(time()-times).strftime("%M:%S:%f"))
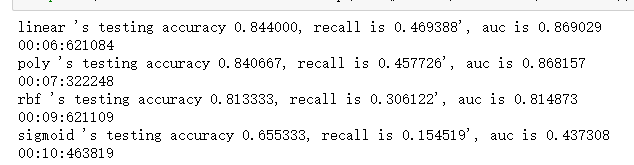
我们注意到,模型的准确度和auc面积还是勉勉强强,但是每个核函数下的recall都不太高。相比之下,其实线性模型的效果是最好的。那现在我们可以开始考虑了,在这种状况下,我们要向着什么方向进行调参呢?我们最想要的是什么?
我们可以有不同的目标:
一,我希望不计一切代价判断出少数类,得到最高的recall。
二,我们希望追求最高的预测准确率,一切目的都是为了让accuracy更高,我们不在意recall或者AUC。
三,我们希望达到recall,ROC和accuracy之间的平衡,不追求任何一个也不牺牲任何一个。
4.5 模型调参
4.5.1 最求最高Recall
如果我们想要的是最高的recall,可以牺牲我们准确度,希望不计一切代价来捕获少数类,那我们首先可以打开我们的class_weight参数,使用balanced模式来调节我们的recall:
times = time()
for kernel in ["linear","poly","rbf","sigmoid"]:
clf = SVC(kernel = kernel
,gamma="auto"
,degree = 1
,cache_size = 5000
,class_weight = "balanced"
).fit(Xtrain, Ytrain)
result = clf.predict(Xtest)
score = clf.score(Xtest,Ytest)
recall = recall_score(Ytest, result)
auc = roc_auc_score(Ytest,clf.decision_function(Xtest))
print("%s 's testing accuracy %f, recall is %f', auc is %f" % (kernel,score,recall,auc))
print(datetime.datetime.fromtimestamp(time()-times).strftime("%M:%S:%f"))

在锁定了线性核函数之后,我甚至可以将class_weight调节得更加倾向于少数类,来不计代价提升recall。
times = time()
clf = SVC(kernel = "linear"
,gamma="auto"
,cache_size = 5000
,class_weight = {1:15} #注意,这里写的其实是,类别1:10,隐藏了类别0:1这个比例
).fit(Xtrain, Ytrain)
result = clf.predict(Xtest)
score = clf.score(Xtest,Ytest)
recall = recall_score(Ytest, result)
auc = roc_auc_score(Ytest,clf.decision_function(Xtest))
print("testing accuracy %f, recall is %f', auc is %f" %(score,recall,auc))
print(datetime.datetime.fromtimestamp(time()-times).strftime("%M:%S:%f"))

随着recall地无节制上升,我们的精确度下降得十分厉害,不过看起来AUC面积却还好,稳定保持在0.86左右。如果此时我们的目的就是追求一个比较高的AUC分数和比较好的recall,那我们的模型此时就算是很不错了。虽然现在,我们的精确度很低,但是我们的确精准地捕捉出了每一个雨天。
4.5.2 追求最高准确率
在我们现有的目标(判断明天是否会下雨)下,追求最高准确率而不顾recall其实意义不大, 但出于练习的目的,我们来看看我们能够有怎样的思路。此时此刻我们不在意我们的Recall了,那我们首先要观察一下,我们的样本不均衡状况。如果我们的样本非常不均衡,但是此时却有很多多数类被判错的话,那我们可以让模型任性地把所有地样本都判断为0,完全不顾少数类。
valuec = pd.Series(Ytest).value_counts()
valuec
#0 1157
#1 343
valuec[0]/valuec.sum()
# 0.7713333333333333
初步判断,可以认为我们其实已经将大部分的多数类判断正确了,所以才能够得到现在的正确率。为了证明我们的判断,我们可以使用混淆矩阵来计算我们的特异度,如果特异度非常高,则证明多数类上已经很难被操作了。
#查看模型的特异度
from sklearn.metrics import confusion_matrix as CM
clf = SVC(kernel = "linear"
,gamma="auto"
,cache_size = 5000
).fit(Xtrain, Ytrain)
result = clf.predict(Xtest)
cm = CM(Ytest,result,labels=(1,0))
cm
specificity = cm[1,1]/cm[1,:].sum()
specificity #几乎所有的0都被判断正确了,还有不少1也被判断正确了
# 0.9550561797752809
可以看到,特异度非常高,此时此刻如果要求模型将所有的类都判断为0,则已经被判断正确的少数类会被误伤,整体的准确率一定会下降。而如果我们希望通过让模型捕捉更多少数类来提升精确率的话,却无法实现,因为一旦我们让模型更加倾向于少数类,就会有更多的多数类被判错。
可以试试看使用class_weight将模型向少数类的方向稍微调整,已查看我们是否有更多的空间来提升我们的准确率。如果在轻微向少数类方向调整过程中,出现了更高的准确率,则说明模型还没有到极限。
irange = np.linspace(0.01,0.05,10)
for i in irange:
times = time()
clf = SVC(kernel = "linear"
,gamma="auto"
,cache_size = 5000
,class_weight = {1:1+i}
).fit(Xtrain, Ytrain)
result = clf.predict(Xtest)
score = clf.score(Xtest,Ytest)
recall = recall_score(Ytest, result)
auc = roc_auc_score(Ytest,clf.decision_function(Xtest))
print("under ratio 1:%f testing accuracy %f, recall is %f', auc is %f" % (1+i,score,recall,auc))
print(datetime.datetime.fromtimestamp(time()-times).strftime("%M:%S:%f"))
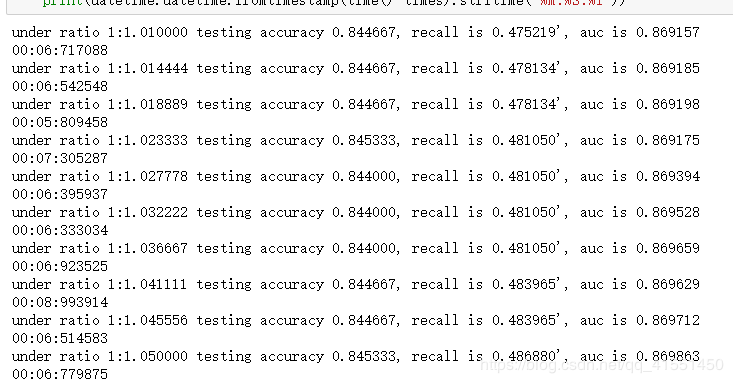
惊喜出现了,我们的最高准确度是84.53%,超过了我们之前什么都不做的时候得到的84.40%。可见,模型还是有
潜力的。我们可以继续细化我们的学习曲线来进行调整:
irange_ = np.linspace(0.018889,0.027778,10)
for i in irange_:
times = time()
clf = SVC(kernel = "linear"
,gamma="auto"
,cache_size = 5000
,class_weight = {1:1+i}
).fit(Xtrain, Ytrain)
result = clf.predict(Xtest)
score = clf.score(Xtest,Ytest)
recall = recall_score(Ytest, result)
auc = roc_auc_score(Ytest,clf.decision_function(Xtest))
print("under ratio 1:%f testing accuracy %f, recall is %f', auc is %f" %(1+i,score,recall,auc))
print(datetime.datetime.fromtimestamp(time()-times).strftime("%M:%S:%f"))
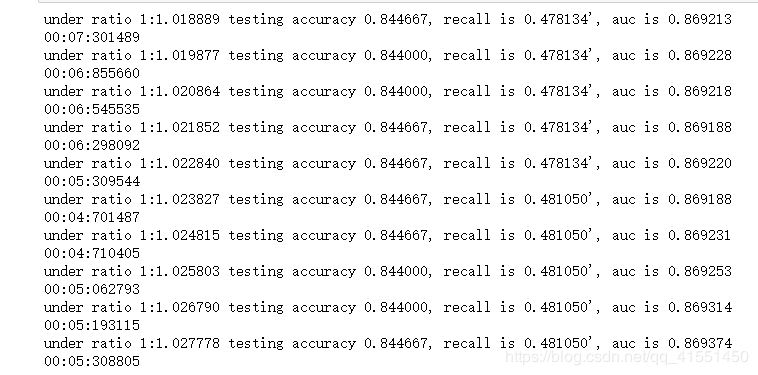
模型的效果没有太好,并没有再出现比我们的84.53%精确度更高的取值。可见,模型在不做样本平衡的情况下,准确度其实已经非常接近极限了,让模型向着少数类的方向调节,不能够达到质变。如果我们真的希望再提升准确度,只能选择更换模型的方式,调整参数已经不能够帮助我们了。想想看什么模型在线性数据上表现最好呢?
from sklearn.linear_model import LogisticRegression as LR
logclf = LR(solver="liblinear").fit(Xtrain, Ytrain)
logclf.score(Xtest,Ytest)
# 0.8486666666666667
C_range = np.linspace(5,10,10)
for C in C_range:
logclf = LR(solver="liblinear",C=C).fit(Xtrain, Ytrain)
print(C,logclf.score(Xtest,Ytest))

尽管我们实现了非常小的提升,但可以看出来,模型的精确度还是没有能够实现质变。也许,要将模型的精确度提升到90%以上,我们需要集成算法:比如,梯度提升树。大家如果感兴趣,可以自己下去试试看。
4.5.3 追求平衡
我们前面经历了多种尝试,选定了线性核,并发现调节class_weight并不能够使我们模型有较大的改善。现在我们来试试看调节线性核函数的C值能否有效果:
###======【TIME WARNING:10mins】======###
import matplotlib.pyplot as plt
C_range = np.linspace(0.01,20,20)
recallall = []
aucall = []
scoreall = []
for C in C_range:
times = time()
clf = SVC(kernel = "linear",C=C,cache_size = 5000
,class_weight = "balanced"
).fit(Xtrain, Ytrain)
result = clf.predict(Xtest)
score = clf.score(Xtest,Ytest)
recall = recall_score(Ytest, result)
auc = roc_auc_score(Ytest,clf.decision_function(Xtest))
recallall.append(recall)
aucall.append(auc)
scoreall.append(score)
print("under C %f, testing accuracy is %f,recall is %f', auc is %f" % (C,score,recall,auc))
print(datetime.datetime.fromtimestamp(time()-times).strftime("%M:%S:%f"))
print(max(aucall),C_range[aucall.index(max(aucall))])
plt.figure()
plt.plot(C_range,recallall,c="red",label="recall")
plt.plot(C_range,aucall,c="black",label="auc")
plt.plot(C_range,scoreall,c="orange",label="accuracy")
plt.legend()
plt.show()
这段代码运行大致需要10分钟时间,因此我给大家我展现一下我运行出来的结果:
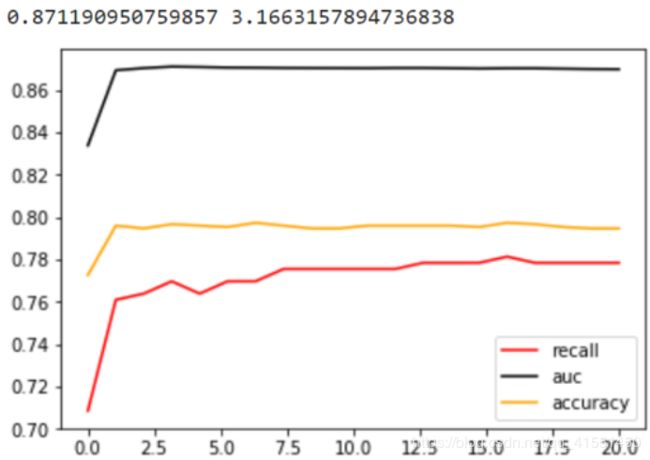
可以观察到几个现象。
首先,我们注意到,随着C值逐渐增大,模型的运行速度变得越来越慢。对于SVM这个本来运行就不快的模型来说,巨大的C值会是一个比较危险的消耗。所以正常来说,我们应该设定一个较小的C值范围来进行调整。
其次,C很小的时候,模型的各项指标都很低,但当C到1以上之后,模型的表现开始逐渐稳定,在C逐渐变大之后,模型的效果并没有显著地提高。可以认为我们设定的C值范围太大了,然而再继续增大或者缩小C值的范围,AUC面积也只能够在0.86上下进行变化了,调节C值不能够让模型的任何指标实现质变。
我们把目前为止最佳的C值带入模型,看看我们的准确率,Recall的具体值:
times = time()
clf = SVC(kernel = "linear",C=3.1663157894736838,cache_size = 5000
,class_weight = "balanced"
).fit(Xtrain, Ytrain)
result = clf.predict(Xtest)
score = clf.score(Xtest,Ytest)
recall = recall_score(Ytest, result)
auc = roc_auc_score(Ytest,clf.decision_function(Xtest))
print("testing accuracy %f,recall is %f', auc is %f" % (score,recall,auc))
print(datetime.datetime.fromtimestamp(time()-times).strftime("%M:%S:%f"))

可以看到,这种情况下模型的准确率,Recall和AUC都没有太差,但是也没有太好,这也许就是模型平衡后的一种结果。现在,光是调整支持向量机本身的参数,已经不能够满足我们的需求了,要想让AUC面积更进一步,我们需要绘制ROC曲线,查看我们是否可以通过调整阈值来对这个模型进行改进。
from sklearn.metrics import roc_curve as ROC
import matplotlib.pyplot as plt
FPR, Recall, thresholds = ROC(Ytest,clf.decision_function(Xtest),pos_label=1)
area = roc_auc_score(Ytest,clf.decision_function(Xtest))
plt.figure()
plt.plot(FPR, Recall, color='red',
label='ROC curve (area = %0.2f)' % area)
plt.plot([0, 1], [0, 1], color='black', linestyle='--')
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('Recall')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()
maxindex = (Recall - FPR).tolist().index(max(Recall - FPR))
thresholds[maxindex]
![]()
基于我们选出的最佳阈值,我们来认为确定y_predict,并确定在这个阈值下的recall和准确度的值:
from sklearn.metrics import accuracy_score as AC
times = time()
clf = SVC(kernel = "linear",C=3.1663157894736838,cache_size = 5000
,class_weight = "balanced"
).fit(Xtrain, Ytrain)
prob = pd.DataFrame(clf.decision_function(Xtest))
prob.loc[prob.iloc[:,0] >= thresholds[maxindex],"y_pred"]=1
prob.loc[prob.iloc[:,0] < thresholds[maxindex],"y_pred"]=0
prob.loc[:,"y_pred"].isnull().sum()
#检查模型本身的准确度
score = AC(Ytest,prob.loc[:,"y_pred"].values)
recall = recall_score(Ytest, prob.loc[:,"y_pred"])
print("testing accuracy %f,recall is %f" % (score,recall))
print(datetime.datetime.fromtimestamp(time()-times).strftime("%M:%S:%f"))
反而还不如我们不调整时的效果好。可见,如果我们追求平衡,那SVC本身的结果就已经非常接近最优结果了。调节阈值,调节参数C和调节class_weight都不一定有效果。但整体来看,我们的模型不是一个糟糕的模型,但这个结果如果提交到kaggle参加比赛是绝对不足够的。如果大家感兴趣,还可以更加深入地探索模型,或者换别的方法来处理特征,以达到AUC面积0.9以上,或是准确度或recall都提升到90%以上。
![]()
4.6 SVM总结&结语
在两周的学习中,我们逐渐探索了SVC在sklearn中的全貌,我们学习了SVM原理,包括决策边界,损失函数,拉格朗日函数,拉格朗日对偶函数,软间隔硬间隔,核函数以及核函数的各种应用。我们了解了SVC类的各种重要参数,属性和接口,其中参数包括软间隔的惩罚系数C,核函数kernel,核函数的相关参数gamma,coef0和degree,解决样本不均衡的参数class_weight,解决多分类问题的参数decision_function_shape,控制概率的参数probability,控制计算内存的参数cache_size,属性主要包括调用支持向量的属性support_vectors_和查看特征重要性的属性coef_。接口中,我们学习了最核心的decision_function。除此之外,我们介绍了分类模型的模型评估指标:混淆矩阵和ROC曲线,还介绍了部分特征工程和数据预处理的思路。
支持向量机是深奥并且强大的模型,我们还可以在很多地方继续进行探索,能够学到这里的大家都非常棒!希望大家再接再厉,掌握好这个强大的算法,后面的学习中继续加油。