机器学习9-降维与度量学习

1. 奇异值分解(SVD)——特征分解

1.1 特征分解

特征值和特征向量的定义如下：
$$Ax=\lambda x$$
其中A是一个n×n的实对称矩阵，x是一个n维向量，则我们说λ是矩阵A的一个特征值，而x是矩阵A的特征值λ所对应的特征向量。
如果我们求出了矩阵A的n个特征值${\lambda }_1\le {\lambda }_2\le ...\le {\lambda }_n$,以及这n个特征值所对应的特征向量$w_1,w_2,...w_n$，，如果这n个特征向量线性无关，那么矩阵A就可以用下式的特征分解表示：
$$A=W\Sigma W^{-1}$$
W是这n个特征向量所张成的n×n维矩阵，而Σ为这n个特征值为主对角线的n×n维矩阵。
一般我们会把W的这n个特征向量标准化，即满足$||w_i|{|}_2=1$, 或者说$w_i^T{w}_i=1$，此时W的n个特征向量为标准正交基，满足$W^{T}W=I$，即$W^T=W^{-1}$, 也就是说W为酉矩阵。这时特征分解表达式可以写成：
$$A=W\Sigma W^T$$

1.2 奇异值分解

SVD也是对矩阵进行分解，但是和特征分解不同，SVD并不要求要分解的矩阵为方阵。假设我们的矩阵A是一个m×n的矩阵，那么我们定义矩阵A的SVD为：
$$A=U\Sigma V^T$$
其中U是一个m×m的矩阵，Σ是一个m×n的矩阵，除了主对角线上的元素以外全为0，主对角线上的每个元素都称为奇异值，V是一个n×n的矩阵。U和V都是酉矩阵，即满足$U^{T}U=I,V^{T}V=I$。

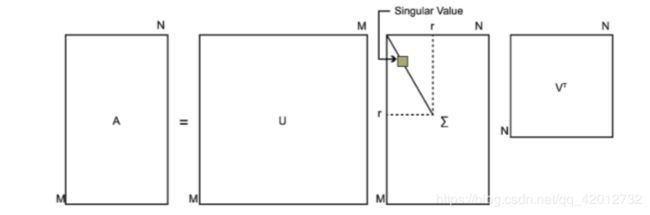
如果我们将A的转置和A做矩阵乘法，那么会得到n×n的一个方阵$A^{T}A$。既然$A^{T}A$是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：
$$(A^{T}A)v_i={\lambda }_i{v}_i$$
将$A^{T}A$的所有特征向量张成一个n×n的矩阵V，就是我们SVD公式里面的V矩阵了。一般我们将V中的每个特征向量叫做A的右奇异向量。
m×m的一个方阵$A{A}^T$
$$(A{A}^T)u_i={\lambda }_i{u}_i$$
将$A{A}^T$的所有特征向量张成一个m×m的矩阵U，就是我们SVD公式里面的U矩阵了。一般我们将U中的每个特征向量叫做A的左奇异向量。
(证明):
$$A=U\Sigma V^T\Rightarrow A^T=V{\Sigma }^T{U}^T\Rightarrow A^{T}A=V{\Sigma }^T{U}^{T}U\Sigma V^T=V{\Sigma }^2{V}^T$$
可以看出$A^{T}A$的特征向量组成的的确就是我们SVD中的V矩阵。类似的方法可以得到$A^{T}A$的特征向量组成的就是我们SVD中的U矩阵。
求出每个奇异值:
$$A=U\Sigma V^T\Rightarrow AV=U\Sigma V^{T}V\Rightarrow AV=U\Sigma \Rightarrow A{v}_i={\sigma }_i{u}_i\Rightarrow {\sigma }_i=A{v}_i/u_i$$
或者:可以通过求出$A^{T}A$的特征值取平方根来求奇异值。
$${\sigma }_i=\sqrt{{\lambda }_i}$$
在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。

2. PCA

在数据压缩消除冗余和数据噪音消除等领域都有广泛的应用。
希望降维的标准：

1. 样本点到这个超平面的距离足够近
2. 样本点在这个超平面上的投影能尽可能的分开。

2.1 PCA基于最小投影距离的推导

我们首先看第一种解释的推导，即样本点到这个超平面的距离足够近。
假设m个n维数据$(x^{(1)},x^{(2)},...,x^{(m)})$都已经进行了中心化，即$\sum _{i=1}^m{x}^{(i)}=0$。经过投影变换后得到的新坐标系为$\{w_1,w_2,...,w_n\}$,其中w是标准正交基，即$||w|{|}_2=1,w_i^T{w}_j=0$。
如果我们将数据从n维降到n’维，即丢弃新坐标系中的部分坐标，则新的坐标系为$\{w_1,w_2,...,w_{n^{\prime }}\}$,样本点x(i)在n’维坐标系中的投影为：$z^{(i)}=(z_1^{(i)},z_2^{(i)},...,z_{n^{\prime }}^{(i)}{)}^T$.其中，$z_j^{(i)}=w_j^T{x}^{(i)}$是x(i)在低维坐标系里第j维的坐标。
如果我们用z(i)来恢复原始数据x(i),则得到的恢复数据${\overline{x}}^{(i)}=\sum _{j=1}^{n^{\prime }}{z}_j^{(i)}{w}_j=W{z}^{(i)}$,其中，W为标准正交基组成的矩阵。
现在我们考虑整个样本集，我们希望所有的样本到这个超平面的距离足够近，即最小化下式：
$$\sum _{i=1}^m||{\overline{x}}^{(i)}-x^{(i)}|{|}_2^2$$
$$\begin{gathered} \sum _{i=1}^m||{\overline{x}}^{(i)}-x^{(i)}|{|}_2^2=\sum _{i=1}^m||W{z}^{(i)}-x^{(i)}|{|}_2^2 \\ =\sum _{i=1}^m(W{z}^{(i)}{)}^T(W{z}^{(i)})-2\sum _{i=1}^m(W{z}^{(i)}{)}^T{x}^{(i)}+\sum _{i=1}^m{x}^{(i)T}{x}^{(i)} \\ =\sum _{i=1}^m{z}^{(i)T}{z}^{(i)}-2\sum _{i=1}^m{z}^{(i)T}{W}^T{x}^{(i)}+\sum _{i=1}^m{x}^{(i)T}{x}^{(i)} \\ =\sum _{i=1}^m{z}^{(i)T}{z}^{(i)}-2\sum _{i=1}^m{z}^{(i)T}{z}^{(i)}+\sum _{i=1}^m{x}^{(i)T}{x}^{(i)} \\ =-\sum _{i=1}^m{z}^{(i)T}{z}^{(i)}+\sum _{i=1}^m{x}^{(i)T}{x}^{(i)} \\ =-tr(W^T（\sum _{i=1}^m{x}^{(i)}{x}^{(i)T})W)+\sum _{i=1}^m{x}^{(i)T}{x}^{(i)} \\ =-tr(W^{T}X{X}^{T}W)+\sum _{i=1}^m{x}^{(i)T}{x}^{(i)} \end{gathered}$$
其中第（1）步用到了${\overline{x}}^{(i)}=W{z}^{(i)}$,第二步用到了平方和展开，第（3）步用到了矩阵转置公式$(AB{)}^T=B^T{A}^T$和$W^{T}W=I$,第（4）步用到了$z^{(i)}=W^T{x}^{(i)}$，第（5）步合并同类项，第（6）步用到了$z^{(i)}=W^T{x}^{(i)}$和矩阵的迹,第7步将代数和表达为矩阵形式。
注意到$\sum _{i=1}^m{x}^{(i)}{x}^{(i)T}$是数据集的协方差矩阵，W的每一个向量wj是标准正交基。而$\sum _{i=1}^m{x}^{(i)}{x}^{(i)T}$是一个常量。最小化上式等价于
$$\underset{W}{argmin}-tr(W^{T}X{X}^{T}W)s.t.W^{T}W=I$$

2.2 PCA的推导:基于最大投影方差

对于任意一个样本x(i)，在新的坐标系中的投影为$W^T{x}^{(i)}$,在新坐标系中的投影方差为$x^{(i)T}W{W}^T{x}^{(i)}$，要使所有的样本的投影方差和最大，也就是最大化$\sum _{i=1}^m{W}^T{x}^{(i)}{x}^{(i)T}W$的迹,即：
　$$\underset{W}{argmax}tr(W^{T}X{X}^{T}W)s.t.W^{T}W=I$$
　利用拉格朗日函数可以得到:$J(W)=tr(W^{T}X{X}^{T}W+\lambda (W^{T}W-I))$
有时候，我们不指定降维后的n’的值，而是换种方式，指定一个降维到的主成分比重阈值t。这个阈值t在（0,1]之间。假如我们的n个特征值为${\lambda }_1\ge {\lambda }_2\ge ...\ge {\lambda }_n$,则n’可以通过下式得到:
$$\frac{\sum _{i=1}^{n^{\prime }}{\lambda }_i}{\sum _{i=1}^n{\lambda }_i}\ge t$$

SVD也可以得到协方差矩阵XTX最大的d个特征向量张成的矩阵，但是SVD有个好处，有一些SVD的实现算法可以不求先求出协方差矩阵XTX，也能求出我们的右奇异矩阵V。也就是说，我们的PCA算法可以不用做特征分解，而是做SVD来完成。这个方法在样本量很大的时候很有效。实际上，scikit-learn的PCA算法的背后真正的实现就是用的SVD，而不是我们我们认为的暴力特征分解。
另一方面，注意到PCA仅仅使用了我们SVD的右奇异矩阵，没有使用左奇异矩阵，那么左奇异矩阵有什么用呢？
假设我们的样本是m×n的矩阵X，如果我们通过SVD找到了矩阵$X{X}^T$最大的d个特征向量张成的m×d维矩阵U，则我们如果进行如下处理：
$$X_{d\times n}^{\prime }=U_{d\times m}^T{X}_{m\times n}$$
　　可以得到一个d×n的矩阵X‘,这个矩阵和我们原来的m×n维样本矩阵X相比，行数从m减到了d，可见对行数进行了压缩。也就是说，左奇异矩阵可以用于行数的压缩。相对的，右奇异矩阵可以用于列数即特征维度的压缩，也就是我们的PCA降维

2.3 PCA的优缺点

PCA算法的主要优点有：

1）仅仅需要以方差衡量信息量，不受数据集以外的因素影响。

2）各主成分之间正交，可消除原始数据成分间的相互影响的因素。

3）计算方法简单，主要运算是特征值分解，易于实现。

PCA算法的主要缺点有：

1）主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强。

2）方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响。

3. 多维缩放MDS算法

若要求原始空间中样本之间的距离在低维空间中得以保持，我们就得到了多维缩放(Multiple Dimensional Scaling)算法。这是一种经典的降维算法。

4. 流形学习

https://blog.csdn.net/chenaiyanmie/article/details/80167649

5. 度量学习

降维的主要目的是找到一个合适的低维空间，在此空间上进行学习比在原始空间进行学习性能更好。 事实上，每个空间对应了在样本属性上定义的一个距离度量，度量学习就在于寻找这个距离度量。
先要学习出距离度量必须先定义一个合适的距离度量形式。对两个样本xi与xj，它们之间的平方欧式距离为：

若各个属性重要程度不一样即都有一个权重，则得到加权的平方欧式距离：

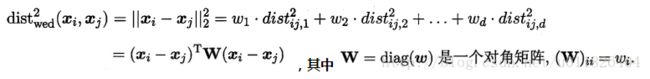
此时各个属性之间都是相互独立无关的(W为对角阵，坐标轴是正交的)，但现实中往往会存在属性之间有关联的情形，例如：身高和体重，一般人越高，体重也会重一些，他们之间存在较大的相关性。这样计算距离就不能分属性单独计算，于是就引入经典的马氏距离（Mahalanobis distance):

矩阵M也称为“度量矩阵”，为保证距离度量的非负性与对称性，M必须为(半)正定对称矩阵，也就是必有正交基P使用$M=P^{T}P$成立，这样就为度量学习定义好了距离度量的形式，换句话说：度量学习便是对度量矩阵M进行学习。现在来回想一下前面我们接触的机器学习不难发现：机器学习算法几乎都是在优化目标函数，从而求解目标函数中的参数。

降维是将原高维空间嵌入到一个合适的低维子空间中，接着在低维空间中进行学习任务；度量学习则是试图去学习出一个距离度量来等效降维的效果，两者都是为了解决维数灾难带来的诸多问题。正是因为在降维算法中，低维子空间的维数d’通常都由人为指定，因此我们需要使用一些低开销的学习器来选取合适的d’，使用KNN来确定。