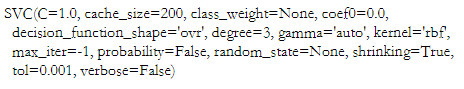svm支持向量机-吴恩达机器学习基于python
文章目录
- 1 线性svm
- 1.1 导入数据
- 1.2 visualize data
- 1.3 svm算法
- 1.3.1训练
- 1.3.2预测
- 2 高斯核函数
- 2.1 高斯核函数
- 2.2 导入数据
- 2.3 visualize data
- 2.4 try build-in Gaussian Kernel of sklearn
- 2.4.1 训练
- 2.4.2 预测
- 2.4.3 画出边界(利用等高线)
- 3 寻找最优参数$C$ & $\sigma$
- 3.1 导入数据
- 3.2 visualize data
- 3.3 manual grid search for $C$ and $\sigma$
- 3.3.1定义参数
- 3.3.2 利用交叉验证集寻找最优参数
- 4 spam filter 垃圾邮件分类器
- 4.1 训练集训练
- 4.2 测试
- 4.2.1 测试集测试
- 4.2.2 文本测试
- 4.2.2.1 文本预处理
- 4.3 与逻辑回归作比较
- 4.3.1 测试集预测
- 4.3.2 邮件文本预测
1 线性svm
所需要的包
import numpy as np
import pandas as pd
import sklearn.svm
import seaborn as sns
import scipy.io as sio #读取matlab的mat数据
import matplotlib.pyplot as plt
1.1 导入数据
mat = sio.loadmat(r'D:\python_try\5. AndrewNg_ML\data\svm\ex6data1.mat')
data = pd.DataFrame(mat.get('X'), columns=['X1', 'X2'])
data['y'] = mat.get('y')
positive:1;negative:0
方便画图
positive = data[data['y'].isin([1])]
negative = data[data['y'].isin([0])]
1.2 visualize data
fig, ax = plt.subplots(figsize=(6,4))
ax.scatter(positive['X1'], positive['X2'], s=50, marker='x', label='Positive')
ax.scatter(negative['X1'], negative['X2'], s=50, marker='o', label='Negative')
ax.legend()
ax.set_title('Raw data')
ax.set_xlabel('X1')
ax.set_ylabel('X2')
plt.show()
1.3 svm算法
使用已有的包sklearn.svm来训练和预测
sklearn.svm中线性svm参考网址
1.3.1训练
C=1
# 调用sklearn.svm线性svm函数
svc1 = sklearn.svm.LinearSVC(C=1, loss='hinge')
svc1
# 训练
svc1.fit(data[['X1', 'X2']], data['y'])
# Returns the mean accuracy on the given test data and labels.返回测试结果和标签的平均误差
svc1.score(data[['X1', 'X2']], data['y'])
0.9803921568627451
C=100
svc100 = sklearn.svm.LinearSVC(C=100, loss='hinge', max_iter=1000)
svc100.fit(data[['X1', 'X2']], data['y'])
svc100.score(data[['X1', 'X2']], data['y'])
C=1我们得到训练数集的完美分类,但是通过增加C的值,我们创建了一个不再适合数据的决策边界,我们可以通过查看每个预测的置信水平来看出这一点,这是该点与超平面距离的函数
1.3.2预测
- decision_function:测试样本的置信度得分
- predict:预测标签
## C = 1
data['SVM1 Confidence'] = svc1.decision_function(data[['X1', 'X2']])
data['SVM1 Predict'] = svc1.predict(data[['X1', 'X2']])
## C = 100
data['SVM100 Confidence'] = svc100.decision_function(data[['X1', 'X2']])
data['SVM100 Predict'] = svc100.predict(data[['X1', 'X2']])
- coef_:变量的权重(方向向量W)
- intercept_:截距项b
# 变量的权重(方向向量W)
Weight1 = svc1.coef_
Weight100 = svc100.coef_
# 截距项b
b1 = svc1.intercept_
b100 = svc100.intercept_
Weight1: [[0.59213514 0.81626829]]
Weight100: [[1.23422417 3.08565111]]
b1: [-4.11515251]
b100: [-12.30774519]
W x + b = 0 Wx+b=0 Wx+b=0
根据公式编写边界函数
## 边界函数
def boundary(Weight, b):
y = -Weight[0][0]/Weight[0][1]*x - b/Weight[0][1]
return y
画图
x = np.linspace(data['X1'].min(), data['X1'].max())
fig = plt.figure(figsize=(12,4))
ax1 = fig.add_subplot(1,2,1)
ax2 = fig.add_subplot(1,2,2)
ax1.scatter(data['X1'], data['X2'], s=50, c=data['SVM1 Predict'], cmap='seismic', label='Predict')
# y1 = -Weight1[0][0]/Weight1[0][1]*x - b1/Weight1[0][1]
y1 = boundary(Weight1, b1)
ax1.plot(x, y1, 'r' , label='Boundary')
ax1.set_title('SVM (C=1) Decision Predict')
ax2.scatter(data['X1'], data['X2'], s=50, c=data['SVM100 Predict'], cmap='seismic', label='Predict')
# y100 = -Weight100[0][0]/Weight100[0][1]*x - b100/Weight100[0][1]
y100 = boundary(Weight100, b100)
ax2.plot(x, y100, 'r' , label='Boundary')
ax2.set_title('SVM (C=100) Decision Predict')
ax1.legend()
ax2.legend()
plt.show()
2 高斯核函数
所需要的包
import matplotlib.pyplot as plt
import numpy as np
import scipy.io as sio # 读取mat数据
import pandas as pd
import seaborn as sns # 画图
from sklearn import svm
2.1 高斯核函数
def gaussian_kernel(x1, x2, sigma):
return np.exp(-np.power(x1-x2, 2).sum()/(2*sigma**2))
x1 = np.array([1, 2, 1])
x2 = np.array([0, 4, -1])
sigma = 2
gaussian_kernel(x1, x2, sigma)
0.32465246735834974
2.2 导入数据
mat = sio.loadmat(r'D:\python_try\5. AndrewNg_ML\data\svm\ex6data2.mat')
data = pd.DataFrame(mat.get('X'), columns=['X1', 'X2'])
data['y'] = mat.get('y')
2.3 visualize data
画图包seaborn例子参考网址
scatterplot画散点图的不存在了
sns.set(style='white')
sns.lmplot(x="X1", y="X2", hue="y", data=data, markers=["x", "o"], fit_reg=False, scatter_kws={'s':10})
2.4 try build-in Gaussian Kernel of sklearn
尝试创建一个高斯内核模型
2.4.1 训练
svm.SVC参考网址
# 查看参数设置
svm.SVC()
高斯核函数: e x p ( − ∣ ∣ x − l ∣ ∣ 2 2 σ 2 ) exp(-\frac{||x-l||^2}{2\sigma^2}) exp(−2σ2∣∣x−l∣∣2)
其中, g a m m a = 1 2 σ 2 gamma=\frac{1}{2\sigma^2} gamma=2σ21
C = 1
svc1 = svm.SVC(C=1, kernel='rbf', gamma=10, probability=True)
svc1.fit(data[['X1', 'X2']], data['y'])
svc1.score(data[['X1', 'X2']], data['y'])
0.9698725376593279
C = 100
svc100 = svm.SVC(C=100, kernel='rbf', gamma=10, probability=True)
svc100.fit(data[['X1', 'X2']], data['y'])
svc100.score(data[['X1', 'X2']], data['y'])
0.9895712630359212
C较大时,可能会导致过拟合,高方差
C较小时,可能会导致欠拟合,高偏差
σ \sigma σ较大时,可能会导致欠拟合,高偏差
σ \sigma σ较小时,可能会导致过拟合,高方差
2.4.2 预测
predict1 = svc1.predict(data[['X1', 'X2']])
predict100 = svc100.predict(data[['X1', 'X2']])
画图
fig = plt.figure(figsize=(8,4))
ax1 = fig.add_subplot(1,2,1)
ax2 = fig.add_subplot(1,2,2)
ax1.scatter(data['X1'], data['X2'], s=10, c=predict1, cmap='seismic', label='Predict')
ax1.set_title('C=1')
ax2.scatter(data['X1'], data['X2'], s=10, c=predict100, cmap='seismic', label='Predict')
ax2.set_title('C=100')
plt.show()
2.4.3 画出边界(利用等高线)
# 画等高线需要先生成网格
x1 = np.linspace(data['X1'].min(), data['X1'].max(), 100)
x2 = np.linspace(data['X2'].min(), data['X2'].max(), 100)
X1, X2 = np.meshgrid(x1, x2)
grid_points=np.c_[X1.ravel(), X2.ravel()] # np.c_:合并
# C=1,预测
grid_predict1 = svc1.predict(grid_points).reshape(X1.shape)
# C=100,预测
grid_predict100 = svc100.predict(grid_points).reshape(X1.shape)
fig = plt.figure(figsize=(8,4))
ax1 = fig.add_subplot(1,2,1)
ax2 = fig.add_subplot(1,2,2)
ax1.scatter(data['X1'], data['X2'], s=10, c=data['y'], cmap='seismic')
ax1.contour(X1, X2, grid_predict1, colors='black', linewidths=0.5)
ax1.set_title('C=1')
ax2.scatter(data['X1'], data['X2'], s=10, c=data['y'], cmap='seismic')
ax2.contour(X1, X2, grid_predict100, colors='black', linewidths=0.5)
ax2.set_title('C=100')
plt.show()
3 寻找最优参数 C C C & σ \sigma σ
import scipy.io as sio #导入mat数据
import pandas as pd
import matplotlib.pyplot as plt # 画图
import sklearn.svm as svm # 训练svm
import numpy as np
3.1 导入数据
** 训练数据**
mat = sio.loadmat(r'D:\python_try\5. AndrewNg_ML\data\svm\ex6data3.mat')
TrainData = pd.DataFrame(mat.get('X'), columns=['X1', 'X2'])
TrainData['y'] = mat.get('y')
交叉验证数据
cvData = pd.DataFrame(mat.get('Xval'), columns=['X1', 'X2'])
cvData['y'] = mat.get('yval')
3.2 visualize data
TrainPositive = TrainData[TrainData['y'].isin([1])]
TrainNegative = TrainData[TrainData['y'].isin([0])]
# 画图
fig, ax = plt.subplots(figsize=(8,6))
ax.scatter(TrainPositive['X1'], TrainPositive['X2'], marker='x', c='blue', label='Positive')
ax.scatter(TrainNegative['X1'], TrainNegative['X2'], marker='o', c='red', label='Negative')
ax.legend()
plt.show()
3.3 manual grid search for C C C and σ \sigma σ
3.3.1定义参数
参数集合
C C C: {0:01; 0:03; 0:1; 0:3; 1; 3; 10; 30}
σ \sigma σ: {0:01; 0:03; 0:1; 0:3; 1; 3; 10; 30}
# 定义gamma和sigma转换函数
def gamma(sigma):
return 1/(2*sigma**2)
C和gamma集合
candidate = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30]
combination = [(C, gamma(sigma))for C in candidate for sigma in candidate]
3.3.2 利用交叉验证集寻找最优参数
svm.svc参考网址
# 查看参数
svm.SVC()
Score = []
for C, Gamma in combination:
svc = svm.SVC(C=C, gamma=Gamma)
svc.fit(TrainData[['X1', 'X2']], TrainData['y'])
Score.append(svc.score(cvData[['X1', 'X2']], cvData['y']))
# 找最优参数
bestScore = Score[np.argmax(Score)]
bestParameter = combination[np.argmax(Score)]
print("bestScore: ", bestScore)
print("bestParameter: ", bestParameter)
bestScore: 0.965
bestParameter: (1, 49.99999999999999)
因为np.argmax只能返回一个索引,所以参数和吴恩达老师所给的不一样
4 spam filter 垃圾邮件分类器
import scipy.io as sio # load mat
import pandas as pd
from sklearn import svm # svm
from sklearn import metrics # 准确率
from os import listdir # 文件夹中的文件名
import re #regular expression for e-mail processing
import nltk, nltk.stem.porter # 这个英文算法似乎更符合作业里面所用的代码,与上面效果差不多
import numpy as np
from sklearn.linear_model import LogisticRegression # logistic
4.1 训练集训练
TrainMat = sio.loadmat(r'D:\python_try\5. AndrewNg_ML\data\svm\spamTrain.mat')
X_train, y_train = TrainMat.get('X'), TrainMat.get('y').ravel()
svc = svm.SVC()
svc.fit(X_train, y_train)
4.2 测试
4.2.1 测试集测试
# 导入测试集
TestMat = sio.loadmat(r'D:\python_try\5. AndrewNg_ML\data\svm\spamTest.mat')
X_test, y_test = TestMat.get('Xtest'), TestMat.get('ytest').ravel()
# 预测
predict1 = svc.predict(X_test)
# 准确率
print(metrics.classification_report(y_test, predict1))
4.2.2 文本测试
4.2.2.1 文本预处理
- Lower-casing: 把整封邮件转化为小写。
- Stripping HTML: 移除所有HTML标签,只保留内容。
- Normalizing URLs: 将所有的URL替换为字符串 “httpaddr”。
- Normalizing Email Addresses: 所有的地址替换为 “emailaddr”。
- Normalizing Dollars: 所有dollar符号($)替换为“dollar”。
- Normalizing Numbers: 所有数字替换为“number”。
- Word Stemming(词干提取): 将所有单词还原为词源。例如,“discount”, “discounts”, “discounted” and “discounting”都替换为“discount”。
- Removal of non-words: 移除所有非文字类型,所有的空格(tabs, newlines, spaces)调整为一个空格。
做除了7. 和 8. 的邮件处理
def processEmail(email):
email = email.lower() # 1. Lower-casing
email = re.sub('<[^<>]+>' , ' ', email) # 2. Stripping HTML
email = re.sub('(http:|https:)//[^\s]*', 'httpaddr', email) # 3. Normalizing URLS
email = re.sub('[^\s]+@[^\s]+', 'emailaddr', email) # Normalizing Email Addresses
email = re.sub('[$]+', 'dollar',email) # Normalizing dollars
email = re.sub('\d+', 'number', email) #Normalizing Numbers
return email
做剩下两个的处理,并返回单词列表
def email2Tokenlist(email):
tokenList = []
stemmer = nltk.stem.porter.PorterStemmer()
email = processEmail(email)
tokens = re.split('[ \@\$\/\#\.\-\:\&\*\+\=\[\]\?\!\(\)\{\}\,\'\"\>\_\<\;\%]', email)
for token in tokens:
token = re.sub('[^a-zA-Z0-9]', '', token)
# 提取词根
stemmed = stemmer.stem(token)
if not len(token): continue
tokenList.append(stemmed)
return tokenList
词汇表索引
def email2vocabIndex(email, vocab):
token = email2Tokenlist(email)
index = [i for i in range(len(vocab)) if vocab[i] in token]
return index
将email转化成变量形式,词向量
def email2FeatureVector(email):
df = pd.read_table(r'D:\python_try\5. AndrewNg_ML\data\svm\vocab.txt', names=['words'])
vocab = df.as_matrix() # retuen array
vector = np.zeros(len(vocab)) # 向量
vocabIndex = email2vocabIndex(email, vocab)
for i in vocabIndex:
vector[i] = 1
return vector
预测
for name in emailList:
emailName = r'D:\python_try\5. AndrewNg_ML\data\svm\email\%s' %name
#print(emailName)
with open(emailName, 'r') as f:
email = f.read()
vector = pd.DataFrame(email2FeatureVector(email)).T
predict2 = svc.predict(vector)
print("the email %s is predicted as " % name, predict2)
the email emailSample1.txt is predicted as [0]
the email emailSample2.txt is predicted as [0]
the email spamSample1.txt is predicted as [1]
the email spamSample2.txt is predicted as [0]
“spamSample2.txt” 预测错了
4.3 与逻辑回归作比较
4.3.1 测试集预测
logit = LogisticRegression()
logit.fit(X_train, y_train) # 模型训练
pred = logit.predict(X_test) # 预测
print(metrics.classification_report(y_test, pred)) # 验证
4.3.2 邮件文本预测
for name in emailList:
emailName = r'D:\python_try\5. AndrewNg_ML\data\svm\email\%s' %name
print(emailName)
with open(emailName, 'r') as f:
email = f.read()
#print(email)
vector = pd.DataFrame(email2FeatureVector(email)).T
print(np.average(vector))
#print(set(vector))
predict2 = logit.predict(vector)
print("the email %s is predicted as " % name, predict2)
the email emailSample1.txt is predicted as [0]
the email emailSample2.txt is predicted as [0]
the email spamSample1.txt is predicted as [1]
the email spamSample2.txt is predicted as [1]
综上两种比较,logistic回归的效果更好