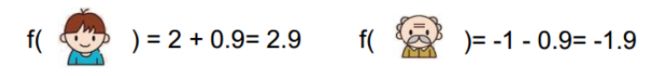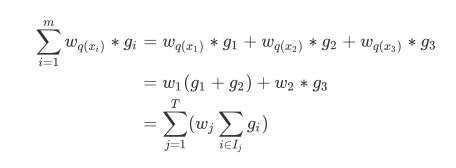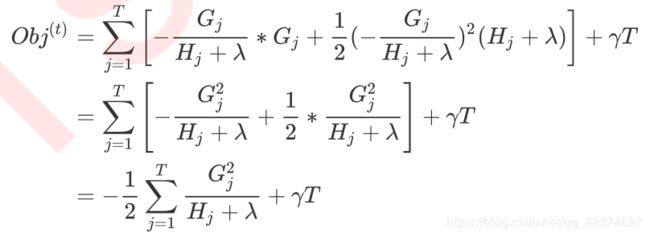sklearn与XGBoost
菜菜的scikit-learn课堂——sklearn与XGBoost
文章目录
- 1. XGBoost简介
- 1.1 xgboost库与XGB的sklearn API
- 1.2 XGBoost的三大板块
- 2 梯度提升树
- 2.1 提升集成算法:重要参数n_estimators
- 2.2 有放回随机抽样:重要参数subsample
- 2.3 迭代决策树:重要参数eta
- 3 XGBoost的智慧
- 3.1 选择弱评估器:重要参数booster
- 3.2 XGB的目标函数:重要参数objective
- 3.3 求解XGB的目标函数
- 3.4 参数化决策树 f k ( x ) f_k\left( x \right) fk(x):参数alpha,lambda
- 3.5 寻找最佳树结构:求解 ω \omega ω与T
- 3.6 寻找最佳分枝:结构分数之差
- 3.7 让树停止生长:重要参数gamma
- 4 XGBoost应用中的其他问题
- 4.1 过拟合:剪枝参数与回归模型调参
- 4.2 XGBoost模型的保存和调用
- 4.2.1 使用Pickle保存和调用模型
- 4.2.2 使用Joblib保存和调用模型
- 4.3 分类案例:XGB中的样本不均衡问题
- 4.4 XGBoost类中的其他参数和功能
1. XGBoost简介
XGBoost算法
XGBoost
XGBoost 是 “Extreme Gradient Boosting”的简称,可译为极限梯度提升算法。
说到XGBoost,不得不提GBDT(Gradient Boosting Decision Tree)。因为XGBoost本质上还是一个GBDT,但是力争把速度和效率发挥到极致,所以叫X (Extreme) GBoosted。包括前面说过,两者都是boosting方法。
XGBoost是一种基于决策树的集成机器学习算法,使用梯度上升框架,适用于分类和回归问题,并且主要是用来解决有监督学习问题
所谓集成学习,是指构建多个分类器(弱分类器)对数据集进行预测,然后用某种策略将多个分类器预测的结果集成起来,作为最终预测结果。
集成学习很好的避免了单一学习模型带来的过拟合问题
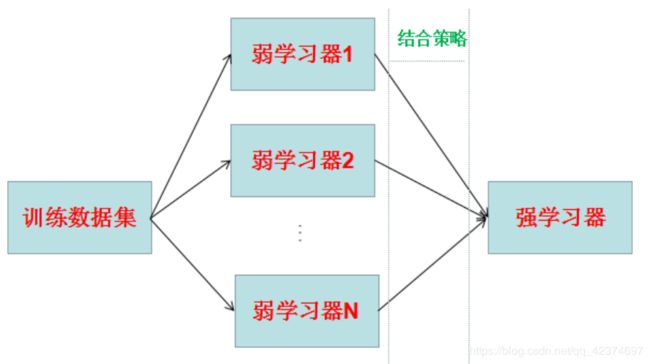
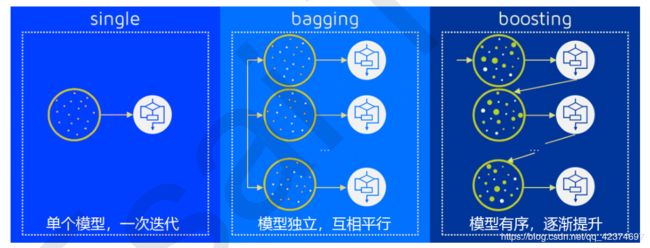
集成学习按照各个弱学习器之间是否存在依赖关系可以分为两类:
- 一个是个体学习器之间存在强依赖关系,必须串行化生成的序列化方法,代表算法就是是boosting系列算法(提升法)。
- 另一类是个体学习器之间不存在强依赖关系,可以并行化生成每个个体学习器,代表算法是bagging和随机森林(Random Forest)系列算法(袋装法)。
因为XGBoost是一种提升树模型,所以它是将许多树模型集成在一起,形成一个很强的分类器。而所用到的树模型则是CART回归树模型。
优点是速度快、效果好、能处理大规模数据、支持多种语言、支持自定义损失函数等
和传统的梯度提升算法相比,XGBoost进行了许多改进,它能够比其他使用梯度提升的集成算法更加快速,并且已经被认为是在分类和回归上都拥有超高性能的先进评估器。
1.1 xgboost库与XGB的sklearn API
安装
pip install -i https://pypi.tuna.tsinghua.edu.cn/simple xgboost
有两种方式可以来使用我们的xgboost库。
第一种方式,是直接使用xgboost库自己的建模流程。
其中最核心的,是DMtarix这个读取数据的类,以及train()这个用于训练的类。
与sklearn把所有的参数都写在类中的方式不同,xgboost库中必须先使用字典设定参数集,再使用train来将参数及输入,然后进行训练。会这样设计的原因,是因为XGB所涉及到的参数实在太多,全部写在xgb.train()中太长也容易出错。
params 可能的取值以及 xgboost.train 的列表
params {eta, gamma, max_depth, min_child_weight, max_delta_step, subsample, colsample_bytree,
colsample_bylevel, colsample_bynode, lambda, alpha, tree_method string, sketch_eps, scale_pos_weight, updater,
refresh_leaf, process_type, grow_policy, max_leaves, max_bin, predictor, num_parallel_tree}
xgboost.train (params, dtrain, num_boost_round=10, evals=(), obj=None, feval=None, maximize=False,
early_stopping_rounds=None, evals_result=None, verbose_eval=True, xgb_model=None, callbacks=None,
learning_rates=None)
第二种方法,使用xgboost库中的sklearn的API
可以调用如下的类,并用 sklearn 当中惯例的实例化,fit 和 predict 的流程来运行XGB,并且也可以调用属性比如coef_等等。
当然,这是回归的类,也有用于分类,用于排序的类。它们与回归的类非常相似,因此了解一个类即可。
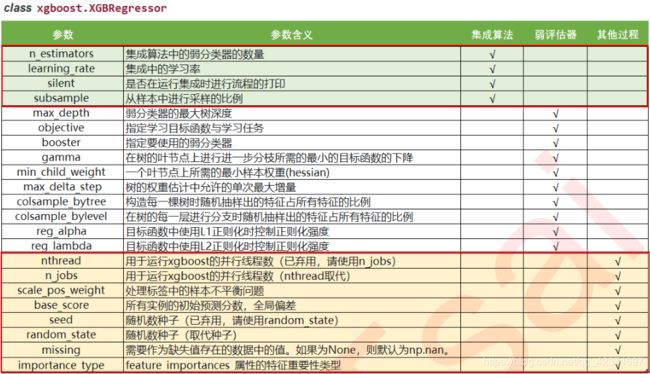
class xgboost.XGBRegressor (
max_depth=3, learning_rate=0.1,
n_estimators=100, silent=True,objective='reg:linear',
booster='gbtree', n_jobs=1, nthread=None,
gamma=0, min_child_weight=1, max_delta_step=0,
subsample=1, colsample_bytree=1, colsample_bylevel=1,
reg_alpha=0, reg_lambda=1, scale_pos_weight=1,
base_score=0.5, random_state=0, seed=None,
missing=None, importance_type='gain', **kwargs)
调用xgboost.train和调用sklearnAPI中的类XGBRegressor,需要输入的参数是不同的,而且看起来相当的不同。但其实,这些参数只是写法不同,功能是相同的。
使用xgboost中设定的建模流程来建模,和使用sklearnAPI中的类来建模,模型效果是比较相似的,但是xgboost库本身的运算速度(尤其是交叉验证)以及调参手段比sklearn要简单。
1.2 XGBoost的三大板块
XGBoost 核心是基于梯度提升树实现的集成算法,整体来说可以有三个核心部分:集成算法本身,用于集成的弱评估器,以及应用中的其他过程。三个部分中,前两个部分包含了XGBoost的核心原理以及数学过程,最后的部分主要是在XGBoost应用中占有一席之地。

2 梯度提升树
2.1 提升集成算法:重要参数n_estimators
XGBoost的基础是梯度提升算法
梯度提升(Gradient boosting)是构建预测模型的最强大技术之一,它是集成算法中提升法(Boosting)的代表算法。
集成算法通过在数据上构建多个弱评估器,汇总所有弱评估器的建模结果,以获取比单个模型更好的回归或分类表现。弱评估器被定义为是表现至少比随机猜测更好的模型,即预测准确率不低于50%的任意模型。
XGBoost中所有的树都是二叉的。
Boosting算法
XGBoost是boosting算法的其中一种。
Boosting算法的思想是将许多弱分类器集成在一起形成一个强分类器。在Boosting算法中,每一个样本数据是有权重的,每一个学习器是有先后顺序的。
梯度提升回归树是专注于回归的树模型的提升集成模型,其建模过程大致如下:最开始先建立一棵树,然后逐渐迭代,每次迭代过程中都增加一棵树,逐渐形成众多树模型集成的强评估器。(每一棵树的生成都是基于前面树的预测结果来进行的,在提升算法中,每一棵树之间不是相互独立,而是相互递进关系)
对于决策树而言,每个被放入模型的任意样本 i 最终一个都会落到一个叶子节点上。而对于回归树,每个叶子节点上的值是这个叶子节点上所有样本的均值。
对于梯度提升回归树来说,每个样本的预测结果可以表示为所有树上的结果的加权求和:
y ^ i ( k ) = ∑ k = 1 K γ k h k ( x i ) \hat{y}_{i}^{\left( k \right)}=\sum_{k=1}^K{\gamma _kh_k\left( x_i \right)} y^i(k)=k=1∑Kγkhk(xi)
其中,K 是树的总数量,k 代表第 k 棵树, γ k \gamma _k γk 是这棵树的权重, h k h_k hk 表示这棵树上的预测结果。
值得注意的是,XGB作为GBDT的改进,在 y ^ \hat{y} y^ 上却有所不同。
对于XGB来说,每个叶子节点上会有一个预测分数(prediction score),也被称为叶子权重。这个叶子权重就是所有在这个叶子节点上的样本在这一棵树上的回归取值,用 f k ( x i ) f_k\left( x_i \right) fk(xi) 或者 ω \omega ω 来表示,其中 f k f_k fk 表示第 k 棵决策树, x i x_i xi 表示样本 i 对应的特征向量。当只有一棵树的时候,就是提升集成算法返回的结果,但这个结果往往非常糟糕。当有多棵树的时候,集成模型的回归结果就是所有树的预测分数之和,假设这个集成模型中总共有 K 棵决策树,则整个模型在这个样本 i 上给出的预测结果为:
y ^ i ( k ) = ∑ k = 1 K f k ( x i ) \hat{y}_{i}^{\left( k \right)}=\sum_{k=1}^K{f_k\left( x_i \right)} y^i(k)=k=1∑Kfk(xi)
XGB vs GBDT 核心区别1:求解预测值 y ^ \hat{y} y^ 的方式不同
GBDT中预测值是由所有弱分类器上的预测结果的加权求和,其中每个样本上的预测结果就是样本所在的叶子节点的均值。而XGBT中的预测值是所有弱分类器上的叶子权重直接求和得到,计算叶子权重是一个复杂的过程。
在集成中我们需要的考虑的第一件事是我们的超参数 K ,究竟要建多少棵树呢?
在随机森林中:n_estimators越大,模型的学习能力就会越强,模型也越容易过拟合。在随机森林中调整的第一个参数就是n_estimators,这个参数非常强大,常常能够一次性将模型调整到极限。
在XGB中,我们也期待相似的表现,虽然XGB的集成方式与随机森林不同,但使用更多的弱分类器来增强模型整体的学习能力这件事是一致的。
建模
# 导入需要的库,模块以及数据
from xgboost import XGBRegressor as XGBR
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.linear_model import LinearRegression as LinearR
from sklearn.datasets import load_boston
from sklearn.model_selection import KFold, cross_val_score as CVS, train_test_split as TTS
from sklearn.metrics import mean_squared_error as MSE
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from time import time
import datetime
data = load_boston()
#波士顿数据集非常简单,但它所涉及到的问题却很多
X = data.data
y = data.target
# 建模,查看其他接口和属性
Xtrain,Xtest,Ytrain,Ytest = TTS(X,y,test_size=0.3,random_state=420)
# s实例化 训练
# 先建100棵树
reg = XGBR(n_estimators=100).fit(Xtrain,Ytrain)
reg.predict(Xtest) #传统接口predict
Ytest.shape # (152,)
reg.predict(Xtest).shape # (152,)
reg.score(Xtest,Ytest) # 0.9050988954757183 返回的是R平方
# 均方误差
MSE(Ytest,reg.predict(Xtest)) # 8.830916470718748 均方误差还是比较大
reg.feature_importances_
#树模型的优势之一:能够查看模型的重要性分数,可以使用嵌入法进行特征选择
'''
array([0.01902167, 0.0042109 , 0.01478317, 0.00553536, 0.02222195,
0.37914094, 0.01679687, 0.04698721, 0.04073574, 0.05491758,
0.0668422 , 0.00869463, 0.32011184], dtype=float32)
'''
交叉验证,与线性回归&随机森林回归进行对比
reg = XGBR(n_estimators=100)
# 交叉验证导入没有进过训练的模型
CVS(reg,Xtrain,Ytrain,cv=5).mean() # 0.7995062802699481 R平方 指标
#放 训练集 的交叉验证 才是更为严谨的交叉验证
CVS(reg,Xtrain,Ytrain,cv=5,scoring='neg_mean_squared_error').mean()
# -16.215644658473447 负的均方误差
#来查看一下sklearn中所有的模型评估指标
import sklearn
sorted(sklearn.metrics.SCORERS.keys())
'''
['accuracy',
'adjusted_mutual_info_score',
'adjusted_rand_score',
'average_precision',
'balanced_accuracy',
'completeness_score',
'explained_variance',
'f1',
'f1_macro',
'f1_micro',
'f1_samples',
'f1_weighted',
'fowlkes_mallows_score',
'homogeneity_score',
'jaccard',
'jaccard_macro',
'jaccard_micro',
'jaccard_samples',
'jaccard_weighted',
'max_error',
'mutual_info_score',
'neg_brier_score',
'neg_log_loss',
'neg_mean_absolute_error',
'neg_mean_gamma_deviance',
'neg_mean_poisson_deviance',
'neg_mean_squared_error',
'neg_mean_squared_log_error',
'neg_median_absolute_error',
'neg_root_mean_squared_error',
'normalized_mutual_info_score',
'precision',
'precision_macro',
'precision_micro',
'precision_samples',
'precision_weighted',
'r2',
'recall',
'recall_macro',
'recall_micro',
'recall_samples',
'recall_weighted',
'roc_auc',
'roc_auc_ovo',
'roc_auc_ovo_weighted',
'roc_auc_ovr',
'roc_auc_ovr_weighted',
'v_measure_score']
'''
# XGBoost
reg = XGBR(n_estimators=100)
CVS(reg,Xtrain,Ytrain,cv=5).mean() # 0.7995062802699481
CVS(reg,Xtrain,Ytrain,cv=5,scoring='neg_mean_squared_error').mean()
# -16.215644658473447
#随机森林
rfr = RFR(n_estimators=100)
CVS(rfr,Xtrain,Ytrain,cv=5).mean() # 0.8080288796090171
CVS(rfr,Xtrain,Ytrain,cv=5,scoring='neg_mean_squared_error').mean()
# -16.9376597094165
# 线性回归
lr = LinearR()
CVS(lr,Xtrain,Ytrain,cv=5).mean() # 0.6835070597278081
CVS(lr,Xtrain,Ytrain,cv=5,scoring='neg_mean_squared_error').mean()
# -25.34950749364843
这里XGBoost略逊于随机森林
#开启参数slient:在数据巨大,预料到算法运行会非常缓慢的时候可以使用这个参数来监控模型的训练进度
reg = XGBR(n_estimators=10,silent=False)
CVS(reg,Xtrain,Ytrain,cv=5,scoring='neg_mean_squared_error').mean()
定义绘制以训练样本数为横坐标的学习曲线的函数
def plot_learning_curve(estimator,title, # 分类器
X, y, # # 特征矩阵和标签
ax=None, #选择子图
ylim=None, #设置纵坐标的取值范围
cv=None, #交叉验证
n_jobs=None #设定索要使用的线程
):
'''
一次性画出所有学习曲线
'''
from sklearn.model_selection import learning_curve
import matplotlib.pyplot as plt
import numpy as np
train_sizes, train_scores, test_scores = learning_curve(estimator, X, y
,shuffle=True # 是否打乱数据
,cv=cv
,random_state=420
,n_jobs=n_jobs)
'''
train_sizes 训练集上的样本数量
train_scores 模型在训练集上交叉验证的分数
test_scores
'''
if ax == None:
ax = plt.gca()
else:
ax = plt.figure()
ax.set_title(title)
if ylim is not None:
ax.set_ylim(*ylim)
ax.set_xlabel("Training examples")
ax.set_ylabel("Score")
ax.grid() #绘制网格,不是必须
ax.plot(train_sizes, np.mean(train_scores, axis=1), 'o-', color="r",label="Training score")
ax.plot(train_sizes, np.mean(test_scores, axis=1), 'o-', color="g",label="Test score")
ax.legend(loc="best")
return ax
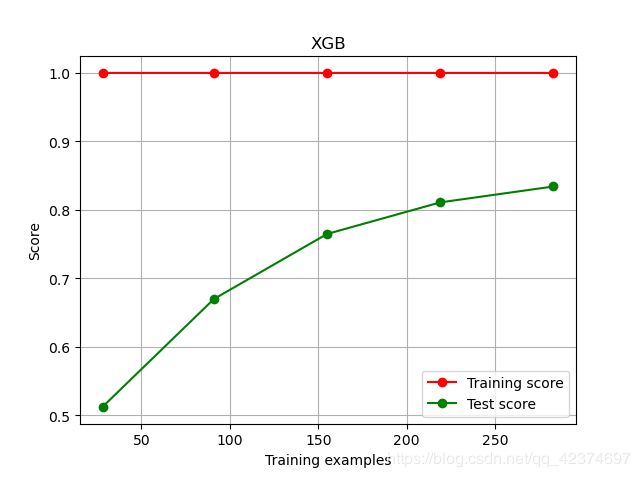
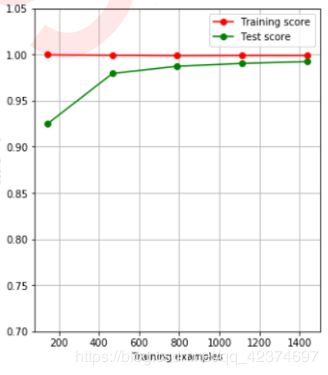
使用学习曲线观察XGB在波士顿数据集上的潜力
# 交叉验证模式 5折 shuffle = True是否打乱数据
cv = KFold(n_splits=5, shuffle = True, random_state=42)
# 调用函数
# 模型为 XGBR(n_estimators=100,random_state=420)
plot_learning_curve(XGBR(n_estimators=100,random_state=420),"XGB",Xtrain,Ytrain,ax=None,cv=cv)
plt.show()
样本非常小时,模型过拟合验证,随着样本量的增加,测试集的分数不断上升,但还是处于过拟合
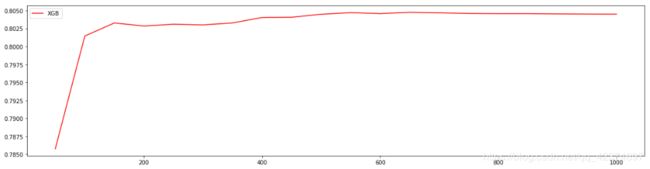
使用参数学习曲线观察n_estimators对模型的影响
axisx = range(10,1010,50)
rs = []
for i in axisx:
reg = XGBR(n_estimators=i,random_state=420)
rs.append(CVS(reg,Xtrain,Ytrain,cv=cv).mean())
print(axisx[rs.index(max(rs))],max(rs))
plt.figure(figsize=(20,5))
plt.plot(axisx,rs,c="red",label="XGB")
plt.legend()
plt.show()
660
0.8046775284172915
选出来的n_estimators非常不寻常,样本也才五百多,就要建立六百多棵树

进化的学习曲线:方差与泛化误差
在机器学习中,我们用来衡量模型在未知数据上的准确率的指标,叫做泛化误差(Genelization error)。
一个集成模型(f)在未知数据集(D)上的泛化误差 E ( f ; D ) E\left( f;D \right) E(f;D) ,由方差(var),偏差(bais)和噪声(e)共同决定。其中偏差就是训练集上的拟合程度决定,方差是模型的稳定性决定,噪音是不可控的。而泛化误差越小,模型就越理想。
E ( f ; D ) = b i a s 2 + v a r + e 2 E\left( f;D \right) =bias^2+var+e^2 E(f;D)=bias2+var+e2
在过去我们往往直接取学习曲线获得的分数的最高点,即考虑偏差最小的点,是因为模型极度不稳定,方差很大的情况其实比较少见。但现在我们的数据量非常少,模型会相对不稳定,因此应当将方差也纳入考虑的范围。
在绘制学习曲线时,不仅要考虑偏差的大小,还要考虑方差的大小,更要考虑泛化误差中我们可控的部分。当然,并不是说可控的部分比较小,整体的泛化误差就一定小,因为误差有时候可能占主导。
改进学习曲线
axisx = range(50,1050,50)
rs = []
var = []
ge = []
for i in axisx:
reg = XGBR(n_estimators=i,random_state=420)
# 交叉验证
cvresult = CVS(reg,Xtrain,Ytrain,cv=cv)
#记录1-偏差
rs.append(cvresult.mean())
#记录方差
var.append(cvresult.var())
#计算泛化误差的可控部分
ge.append((1 - cvresult.mean())**2+cvresult.var())
#打印R2最高所对应的参数取值,并打印这个参数下的方差
print(axisx[rs.index(max(rs))],max(rs),var[rs.index(max(rs))])
#打印方差最低时对应的参数取值,并打印这个参数下的R2
print(axisx[var.index(min(var))],rs[var.index(min(var))],min(var))
#打印泛化误差可控部分的参数取值,并打印这个参数下的R2,方差以及泛化误差的可控部分
print(axisx[ge.index(min(ge))],rs[ge.index(min(ge))],var[ge.index(min(ge))],min(ge))
plt.figure(figsize=(20,5))
plt.plot(axisx,rs,c="red",label="XGB")
plt.legend()
plt.show()
# R2最高的n_estimators R2最高 R2最高所以对应的方差
# 方差最低的n_estimators 方差最低的R2 最低de方差
# 泛化误差最低的n_estimators 泛化误差最低的R2 最低de泛化误差
# R2最高的n_estimators R2最高 R2最高所以对应的方差
650 0.80476050359201 0.01053673846018678
# 方差最低的n_estimators 方差最低的R2 最低de方差
50 0.78577247088309 0.009072727885598212
# 泛化误差最低的n_estimators 泛化误差最低的R2 泛化误差最低的方差 最低de泛化误差
150 0.8032842414878519 0.009747694343514357 0.04844478399052411
细化学习曲线,找出最佳n_estimators
axisx = range(100,300,10)
rs = []
var = []
ge = []
for i in axisx:
reg = XGBR(n_estimators=i,random_state=420)
cvresult = CVS(reg,Xtrain,Ytrain,cv=cv)
rs.append(cvresult.mean())
var.append(cvresult.var())
ge.append((1 - cvresult.mean())**2+cvresult.var())
print(axisx[rs.index(max(rs))],max(rs),var[rs.index(max(rs))])
print(axisx[var.index(min(var))],rs[var.index(min(var))],min(var))
print(axisx[ge.index(min(ge))],rs[ge.index(min(ge))],var[ge.index(min(ge))],min(ge))
rs = np.array(rs)
var = np.array(var)*0.01
plt.figure(figsize=(20,5))
plt.plot(axisx,rs,c="black",label="XGB")
#添加方差线 R2加减方差
plt.plot(axisx,rs+var,c="red",linestyle='-.')
plt.plot(axisx,rs-var,c="red",linestyle='-.')
plt.legend()
plt.show()
180 0.8038787848970184 0.00959321570484315
180 0.8038787848970184 0.00959321570484315
180 0.8038787848970184 0.00959321570484315 0.04805674671831314
plt.figure(figsize=(20,5))
plt.plot(axisx,ge,c="gray",linestyle='-.')
plt.show()
检测模型效果
time0 = time()
print(XGBR(n_estimators=100,random_state=420).fit(Xtrain,Ytrain).score(Xtest,Ytest))
print(time()-time0)
'''
0.9197580267581366
0.0787498950958252
'''
time0 = time()
print(XGBR(n_estimators=660,random_state=420).fit(Xtrain,Ytrain).score(Xtest,Ytest))
print(time()-time0)
'''
0.9208745746309475
0.36807847023010254
'''
time0 = time()
print(XGBR(n_estimators=180,random_state=420).fit(Xtrain,Ytrain).score(Xtest,Ytest))
print(time()-time0)
'''
0.9231068620728082
0.12366437911987305
'''
总结
-
第一,XGB中的树的数量决定了模型的学习能力,树的数量越多,模型的学习能力越强。只要XGB中树的数量足够了,即便只有很少的数据, 模型也能够学到训练数据100%的信息,所以XGB也是天生过拟合的模型。但在这种情况下,模型会变得非常不稳定。
-
第二,XGB中树的数量很少的时候,对模型的影响较大,当树的数量已经很多的时候,对模型的影响比较小,只能有微弱的变化。当数据本身就处于过拟合的时候,再使用过多的树能达到的效果甚微,反而浪费计算资源。当唯一指标或者准确率给出的n_estimators看起来不太可靠的时候,可以改造学习曲线来帮助我们。
-
第三,树的数量提升对模型的影响有极限,最开始模型的表现会随着XGB的树的数量一起提升,但到达某个点之后,树的数量越多,模型的效果会逐步下降,这也说明了暴力增加n_estimators不一定有效果。
这些都和随机森林中的参数n_estimators表现出一致的状态。在随机森林中我们总是先调整n_estimators,当n_estimators的极限已达到,再考虑其他参数,但XGB中的状况明显更加复杂,当数据集不太寻常的时候会更加复杂。这是我们要给出的第一个超参数,因此还是建议优先调整n_estimators,一般都不会建议一个太大的数目,300以下为佳。
2.2 有放回随机抽样:重要参数subsample
确认了有多少棵树之后,我们来思考一个问题:建立了众多的树,怎么就能够保证模型整体的效果变强呢?
集成的目的是为了模型在样本上能表现出更好的效果,所以对于所有的提升集成算法,每构建一个评估器,集成模型的效果都会比之前更好。也就是随着迭代的进行,模型整体的效果必须要逐渐提升,最后要实现集成模型的效果最优。要实现这个目标,可以首先从训练数据上着手。
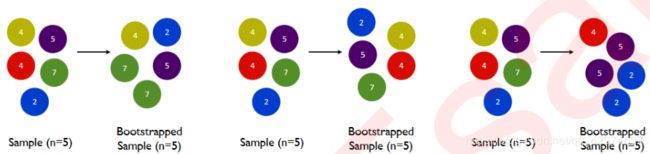
训练模型之前,必然会有一个巨大的数据集。树模型是天生过拟合的模型,并且如果数据量太过巨大,树模型的计算会非常缓慢,因此,要对原始数据集进行有放回抽样(bootstrap)。
有放回的抽样每次只能抽取一个样本,若我们需要总共N个样本,就需要抽取N次。每次抽取一个样本的过程是独立的,这一次被抽到的样本会被放回数据集中,下一次还可能被抽到,因此抽出的数据集中,可能有一些重复的数据。
在无论是装袋bagging还是提升的集成算法中boosting,有放回抽样都是防止过拟合,让单一弱分类器变得更轻量的必要操作。
实际应用中,每次抽取50%左右的数据就能够有不错的效果了。sklearn的随机森林类中也有名为boostrap的参数来帮助我们控制这种随机有放回抽样。同时,这样做还可以保证集成算法中的每个弱分类器(每棵树)都是不同的模型,基于不同的数据建立的自然是不同的模型,而集成一系列一模一样的弱分类器是没有意义的。
在梯度提升树中,每一次迭代都要建立一棵新的树,因此每次迭代中,都要有放回抽取一个新的训练样本。不过,这并不能保证每次建新树后,集成的效果都比之前要好。规定,在梯度提升树中,每构建一个评估器,都让模型更加集中于数据集中容易被判错的那些样本。

首先有一个巨大的数据集,在建第一棵树时,对数据进行初次又放回抽样,然后建模。建模完毕后,对模型进行一个评估,然后将模型预测错误的样本反馈给我们的数据集,一次迭代就算完成。
紧接着,要建立第二棵决策树,于是开始进行第二次又放回抽样。但这次有放回抽样,和初次的随机有放回抽样就不同了,在这次的抽样中,加大了被第一棵树判断错误的样本的权重。也就是说,被第一棵树判断错误的样本,更有可能被我们抽中。
基于这个有权重的训练集来建模,新建的决策树就会更加倾向于这些权重更大的,很容易被判错的样本。
建模完毕之后,又将判错的样本反馈给原始数据集。下一次迭代的时候,被判错的样本的权重会更大,新的模型会更加倾向于很难被判断的这些样本。如此反复迭代,越后面建的树,越是之前的树们判错样本上的专家,越专注于攻克那些之前的树们不擅长的数据。对于一个样本而言,它被预测错误的次数越多,被加大权重的次数也就越多。
只要弱分类器足够强大,随着模型整体不断在被判错的样本上发力,这些样本会渐渐被判断正确。如此就一定程度上实现了我们每新建一棵树模型的效果都会提升的目标。
在sklearn中,使用参数subsample来控制随机抽样。
在xgb和sklearn中,这个参数都默认为1且不能取到0,这说明我们无法控制模型是否进行随机有放回抽样,只能控制抽样抽出来的样本量大概是多少。
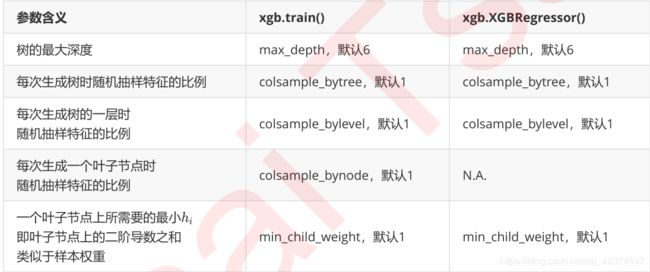
| 参数含义 | xgb.train() | xgb.XGBRegressor() |
|---|---|---|
| 随机抽样的时候抽取的样本比例,范围(0,1] | subsample,默认1 | subsample,默认1 |
在XGBoost中,必须随机抽样(有放回),可以选择抽样的比例,是更接近1,还是更接近0
那除了让模型更加集中于那些困难样本,采样还对模型造成了什么样的影响呢?
采样会减少样本数量,而从学习曲线来看样本数量越少模型的过拟合会越严重,因为对模型来说,数据量越少模型学习越容易,学到的规则也会越具体越不适用于测试样本。
所以subsample参数通常是在样本量本身很大的时候来调整和使用。我们的模型现在正处于样本量过少并且过拟合的状态,根据学习曲线展现出来的规律,训练样本量在200左右的时候,模型的效果有可能反而比更多训练数据的时候好,但这不代表模型的泛化能力在更小的训练样本量下会更强。
正常来说样本量越大,模型才不容易过拟合,现在展现出来的效果,是由于我们的样本量太小造成的一个巧合。从这个角度来看,我们的subsample参数对模型的影响应该会非常不稳定,大概率应该是无法提升模型的泛化能力的,但也不乏提升模型的可能性。
学习曲线:
axisx = np.linspace(0,1,20) # subsample从0-1中取20个数
rs = []
for i in axisx:
reg = XGBR(n_estimators=180,subsample=i,random_state=420)
rs.append(CVS(reg,Xtrain,Ytrain,cv=cv).mean())
print(axisx[rs.index(max(rs))],max(rs))
plt.figure(figsize=(20,5))
plt.plot(axisx,rs,c="green",label="XGB")
plt.legend()
plt.show()
细化学习曲线
axisx = np.linspace(0.05,1,20) # 从0.05-1之间取20个数
rs = [] # 1-偏差
var = [] # 方差
ge = [] # 泛化误差的可控部分
for i in axisx:
reg = XGBR(n_estimators=180,subsample=i,random_state=420)
cvresult = CVS(reg,Xtrain,Ytrain,cv=cv)
rs.append(cvresult.mean())
var.append(cvresult.var())
ge.append((1 - cvresult.mean())**2+cvresult.var())
print(axisx[rs.index(max(rs))],max(rs),var[rs.index(max(rs))])
print(axisx[var.index(min(var))],rs[var.index(min(var))],min(var))
print(axisx[ge.index(min(ge))],rs[ge.index(min(ge))],var[ge.index(min(ge))],min(ge))
rs = np.array(rs)
var = np.array(var)
plt.figure(figsize=(20,5))
plt.plot(axisx,rs,c="black",label="XGB")
plt.plot(axisx,rs+var,c="red",linestyle='-.')
plt.plot(axisx,rs-var,c="red",linestyle='-.')
plt.legend()
plt.show()
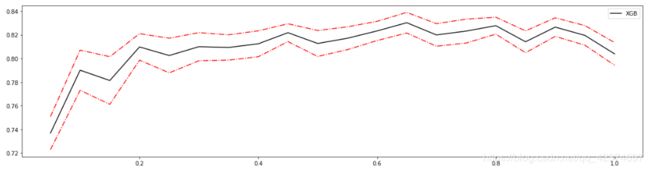
0.65 0.8302530801197368 0.008708816667924316
0.7999999999999999 0.8277414964661117 0.007159903723250457
0.7999999999999999 0.8277414964661117 0.007159903723250457 0.036832895762985055
细化学习曲线
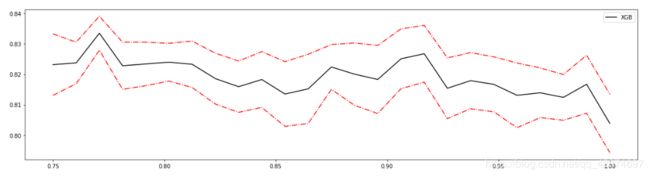
axisx = np.linspace(0.75,1,25) # 0.75-1取25个数
rs = []
var = []
ge = []
for i in axisx:
reg = XGBR(n_estimators=180,subsample=i,random_state=420)
cvresult = CVS(reg,Xtrain,Ytrain,cv=cv)
rs.append(cvresult.mean())
var.append(cvresult.var())
ge.append((1 - cvresult.mean())**2+cvresult.var())
print(axisx[rs.index(max(rs))],max(rs),var[rs.index(max(rs))])
print(axisx[var.index(min(var))],rs[var.index(min(var))],min(var))
print(axisx[ge.index(min(ge))],rs[ge.index(min(ge))],var[ge.index(min(ge))],min(ge))
rs = np.array(rs)
var = np.array(var)
plt.figure(figsize=(20,5))
plt.plot(axisx,rs,c="black",label="XGB")
plt.plot(axisx,rs+var,c="red",linestyle='-.')
plt.plot(axisx,rs-var,c="red",linestyle='-.')
plt.legend()
plt.show()
0.7708333333333334 0.833489187182165 0.005575077682875093
0.7708333333333334 0.833489187182165 0.005575077682875093
0.7708333333333334 0.833489187182165 0.005575077682875093 0.033300928468131166
reg = XGBR(n_estimators=180
# ,subsample=0.7708333333333334
,random_state=420).fit(Xtrain,Ytrain)
reg.score(Xtest,Ytest) # # 0.9050526024842831
MSE(Ytest,reg.predict(Xtest)) # 8.835224213421986
reg = XGBR(n_estimators=180
,subsample=0.7708333333333334
,random_state=420).fit(Xtrain,Ytrain)
reg.score(Xtest,Ytest) # 0.902174931381379
MSE(Ytest,reg.predict(Xtest))
# 9.10300268941902
前面说过,由于我们的样本量太小造成的一个巧合。从这个角度来看,我们的subsample参数对模型的影响应该会非常不稳定,大概率应该是无法提升模型的泛化能力的,但也不乏提升模型的可能性。
参数的效果在我们的预料之中,总体来说这个参数并没有对波士顿房价数据集上的结果造成太大的影响,由于我们的数据集过少,降低抽样的比例反而让数据的效果更低,不如就让它保持默认。
2.3 迭代决策树:重要参数eta
在 2.2 中,加大被前一棵树判断错误的样本的权重
从数据的角度而言,让模型更加倾向于努力攻克那些难以判断的样本。但是,并不是说只要新建了一棵倾向于困难样本的决策树,它就能够帮我把困难样本判断正确了。
困难样本被加重权重是因为前面的树没能把它判断正确,所以对于下一棵树来说,它要判断的测试集的难度,是比之前的树所遇到的数据的难度都要高的,那要把这些样本都
判断正确,会越来越难。
如果新建的树在判断困难样本这件事上还没有前面的树做得好呢?
如果新建的树刚好是一棵特别糟糕的树呢?
所以,除了保证模型逐渐倾向于困难样本的方向,还必须控制新弱分类器的生成,必须保证,每次新添加的树一定得是对这个新数据集预测效果最优的那一棵树。
除了保证模型逐渐倾向于困难样本的方向,怎么保证每次新添加的树一定让集成学习的效果提升?
回顾最优化问题——逻辑回归模型
现在我们希望求解集成算法的最优结果,可以使用同样的思路:
首先找到一个损失函数 Obj ,这个损失函数应该可以通过带入我们的预测结果 y ^ i \hat{y}_i y^i 来衡量梯度提升树在样本的预测效果。然后,利用梯度下降来迭代集成算法:
y ^ i ( k + 1 ) = y ^ i ( k ) + f k + 1 ( x i ) \hat{y}_i^{\left( k+1 \right)}=\hat{y}_i^{\left( k \right)}+f_{k+1}\left( x_i \right) y^i(k+1)=y^i(k)+fk+1(xi)
在 k 次迭代后,集成算法中总共有 k 棵树,k 棵树的集成结果是前面所有树上的叶子权重的累加 ∑ k K f k ( x i ) \sum_k^K{f_k\left( x_i \right)} ∑kKfk(xi) 。所以我们让 k 棵树的集成结果 y ^ i ( k ) \hat{y}_i^{\left( k \right)} y^i(k) 加上新建的树上的叶子权重 f k + 1 ( x i ) f_{k+1}\left( x_i \right) fk+1(xi) ,就可以得到第 k+1 次迭代后,总共 k+1 棵树的预测结果 y ^ i ( k + 1 ) \hat{y}_{i}^{\left( k+1 \right)} y^i(k+1) 了。
我们让这个过程持续下去,直到找到能够让损失函数最小化的 y ^ \hat{y} y^ ,这个 y ^ \hat{y} y^ 就是我们模型的预测结果。
在逻辑回归中参数 θ \theta θ 迭代的时候减去的部分是我们人为规定的步长和梯度相乘的结果。而在GBDT和XGB中,我们却希望能够求解出让预测结果 y ^ \hat{y} y^ 不断迭代的部分 。
在逻辑回归中,我们自定义步长 α \alpha α 来干涉迭代速率,在XGB中看起来却没有这样的设置,但其实不然。在XGB中,完整的迭代决策树的公式应该写作:
y ^ i ( k + 1 ) = y ^ i ( k ) + η f k + 1 ( x i ) \hat{y}_{i}^{\left( k+1 \right)}=\hat{y}_{i}^{\left( k \right)}+\eta f_{k+1}\left( x_i \right) y^i(k+1)=y^i(k)+ηfk+1(xi)
其中 η \eta η 读作"eta",是迭代决策树时的步长(shrinkage),又叫做学习率(learning rate)。和逻辑回归中的 α \alpha α 类似,
- η \eta η 越大,迭代的速度越快,算法的极限很快被达到,有可能无法收敛到真正的最佳。
- η \eta η 越小,越有可能找到更精确的最佳值,更多的空间被留给了后面建立的树,但迭代速度会比较缓慢。
在sklearn中,使用参数 learning_rate 来干涉我们的学习速率( η \eta η):
通常,使用网格搜索来同时调节 n_estimators 和 learning_rate ,确定它们之间的交互效应
定义一个评分函数
def regassess(reg,Xtrain,Ytrain,cv,scoring = ["r2"],show=True):
score = []
for i in range(len(scoring)):
if show:
print("{}:{:.2f}".format(scoring[i] #模型评估指标的名字
,CVS(reg,Xtrain,Ytrain,cv=cv,scoring=scoring[i]).mean()))
score.append(CVS(reg,Xtrain,Ytrain,cv=cv,scoring=scoring[i]).mean())
return score
from time import time
import datetime
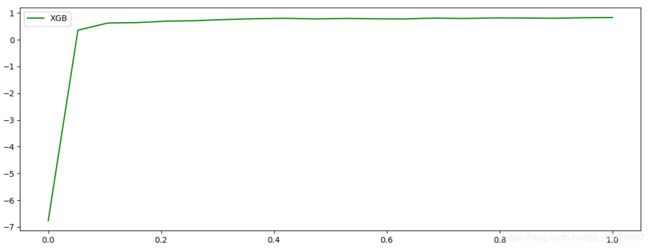
for i in [0,0.2,0.5,1]:
time0=time()
reg = XGBR(n_estimators=180,random_state=420,learning_rate=i)
print("learning_rate = {}".format(i))
regassess(reg,Xtrain,Ytrain,cv,scoring = ["r2","neg_mean_squared_error"])
print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%S:%f"))
print("\t")
'''
learning_rate = 0
r2:-6.76
neg_mean_squared_error:-567.55
00:01:631068
learning_rate = 0.2
r2:0.83
neg_mean_squared_error:-12.30
00:02:656482
learning_rate = 0.5
r2:0.82
neg_mean_squared_error:-12.48
00:01:358224
learning_rate = 1
r2:0.71
neg_mean_squared_error:-20.06
00:01:193319
'''
上面, η \eta η 越大,迭代的速度越快。当 η \eta η =0.2 时,效果最佳
除了运行时间,步长还是一个对模型效果影响巨大的参数,
- 如果设置太大模型就无法收敛(可能导致 R 2 R^2 R2 很小或者MSE很大的情况),
- 如果设置太小模型速度就会非常缓慢,但它最后究竟会收敛到何处很难由经验来判定,
在训练集上表现出来的模样和在测试集上相差甚远,很难直接探索出一个泛化误差很低的步长。
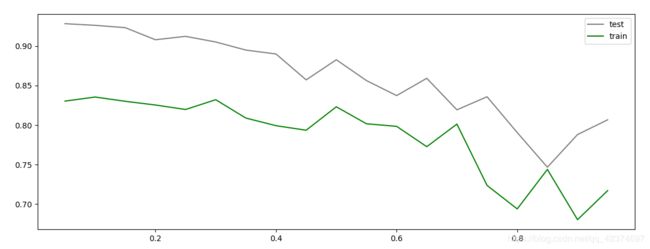
绘制 learning_rate 学习曲线
axisx = np.arange(0.05,1,0.05) # 0.05到1
rs = []
te = []
for i in axisx:
reg = XGBR(n_estimators=180,random_state=420,learning_rate=i)
# 在训练集上的得分
score = regassess(reg,Xtrain,Ytrain,cv,scoring = ["r2","neg_mean_squared_error"],show=False)
# 在测试集上的得分
test = reg.fit(Xtrain,Ytrain).score(Xtest,Ytest)
rs.append(score[0])
te.append(test)
print(axisx[rs.index(max(rs))],max(rs))
plt.figure(figsize=(20,5))
plt.plot(axisx,te,c="gray",label="test")
plt.plot(axisx,rs,c="green",label="train")
plt.legend()
plt.show()
0.1 0.8354667463386021
虽然从图上来说,默认的0.1看起来是一个比较理想的情况,并且看起来更小的步长更利于现在的数据,但我们也无法确定对于其他数据会有怎么样的效果。
所以通常,我们不调整 η \eta η ,即便调整,一般它也会在[0.01,0.2]之间变动。如果希望模型的效果更好,更多的可能是从树本身的角度来说,对树进行剪枝,而不会寄希望于调整 η \eta η。
梯度提升树是XGB的基础,本节中已经介绍了XGB中与梯度提升树的过程相关的四个参数:n_estimators,learning_rate ,silent,subsample。这四个参数的主要目的,其实并不是提升模型表现,更多是了解梯度提升树的原理。现在来看,我们的梯度提升树可是说是由三个重要的部分组成:
- 一个能够衡量集成算法效果的,能够被最优化的损失函数 Obj
- 一个能够实现预测的弱评估器 f k ( x i ) f_k\left( x_i \right) fk(xi)
- 一种能够让弱评估器集成的手段,包括我们讲解的迭代方法,抽样手段,样本加权等等过程
XGBoost是在梯度提升树的这三个核心要素上运行,它重新定义了损失函数和弱评估器,并且对提升算法的集成手段进行了改进,实现了运算速度和模型效果的高度平衡。并且,XGBoost将原本的梯度提升树拓展开来,让XGBoost不再是单纯的树的集成模型,也不只是单单的回归模型。只要我们调节参数,我们可以选择任何我们希望集成的算法,
以及任何我们希望实现的功能。
3 XGBoost的智慧
class xgboost.XGBRegressor (
max_depth=3, learning_rate=0.1,
n_estimators=100, silent=True,
objective='reg:linear',
booster='gbtree',
gamma=0,
reg_alpha=0,
reg_lambda=1,
n_jobs=1, nthread=None,
min_child_weight=1, max_delta_step=0,
subsample=1, colsample_bytree=1, colsample_bylevel=1,
scale_pos_weight=1,
base_score=0.5, random_state=0, seed=None,
missing=None, importance_type='gain', **kwargs)
3.1 选择弱评估器:重要参数booster
梯度提升算法中不只有梯度提升树,XGB作为梯度提升算法的进化,自然也不只有树模型一种弱评估器。
在XGB中,除了树模型,还可以选用线性模型,比如线性回归来进行集成。虽然主流的XGB依然是树模型,但我们也可以使用其他的模型。
基于XGB的这种性质,有参数“booster"来控制究竟使用怎样的弱评估器。

两个参数都默认为"gbtree",如果不想使用树模型,则可以自行调整。当XGB使用线性模型的时候,它的许多数学过程就与使用普通的Boosting集成非常相似
for booster in ["gbtree","gblinear","dart"]:
reg = XGBR(n_estimators=180
,learning_rate=0.1
,random_state=420
,booster=booster).fit(Xtrain,Ytrain)
print(booster)
print(reg.score(Xtest,Ytest))
gbtree
0.9231068620728082
gblinear
0.6286510307485139
dart
0.923106843149575
3.2 XGB的目标函数:重要参数objective
梯度提升算法中都存在着损失函数。不同于逻辑回归和SVM等算法中固定的损失函数写法,集成算法中的损失函数是可选的,要选用什么损失函数取决于我们希望解决什么问题,以及希望使用怎样的模型。
比如说,
- 如果我们的目标是进行回归预测,那我们可以选择调节后的均方误差RMSE作为损失函数。
- 如果我们是进行分类预测,那我们可以选择错误率error或者对数损失log_loss。
只要我们选出的函数是一个可微的,能够代表某种损失的函数,它就可以是XGB中的损失函数。
在众多机器学习算法中,损失函数的核心是衡量模型的泛化能力,即模型在未知数据上的预测的准确与否,我们训练模型的核心目标也是希望模型能够预测准确。
在XGB中,预测准确自然是非常重要的因素,但我们之前提到过,XGB的特点是实现了模型表现和运算速度的平衡的算法。普通的损失函数,比如错误率,均方误差等,都只能够衡量模型的表现,无法衡量模型的运算速度。
回忆一下,我们曾在许多模型中使用空间复杂度和时间复杂度来衡量模型的运算效率。XGB因此引入了模型复杂度来衡量算法的运算效率。
因此XGB的目标函数被写作:传统损失函数 + 模型复杂度。
O b j = ∑ i = 1 m l ( y i , y ^ i ) + ∑ k = 1 K Ω ( f k ) Obj=\sum_{i=1}^m{l\left( y_i,\hat{y}_i \right)}+\sum_{k=1}^K{\varOmega \left( f_k \right)} Obj=i=1∑ml(yi,y^i)+k=1∑KΩ(fk)
其中 i 代表数据集中的第 i 个样本, m 表示导入第 k 棵树的数据总量,K 代表建立的所有树(n_estimators),当只建立了 t 棵树的时候,式子应当为 ∑ k = 1 t Ω ( f k ) \sum_{k=1}^t{\varOmega \left( f_k \right)} ∑k=1tΩ(fk)。
-
第一项代表传统的损失函数,衡量真实标签 y i y_i yi 与预测值 y ^ i \hat{y}_i y^i 之间的差异,通常是RMSE,调节后的均方误差。
-
第二项代表模型的复杂度,使用树模型的某种变换 Ω \varOmega Ω 表示,这个变化代表了一个从树的结构来衡量树模型的复杂度的式子,可以有多种定义。
注意,第二项中没有特征矩阵 X 的介入。我们在迭代每一棵树的过程中,都最小化 Obj 来力求获取最优的 y ^ \hat{y} y^ ,因此我们同时最小化了模型的错误率和模型的复杂度,这种设计目标函数的方法不得不说实在是非常巧妙和聪明。
注意:整个目标函数都与 K 棵树相关
对于,第一项传统损失函数与已经建好的所有树相关的
y ^ i ( t ) = ∑ k t f k ( x i ) = ∑ k t − 1 f k ( x i ) + f t ( x i ) \hat{y}_i^{\left( t \right)}=\sum_k^t{f_k\left( x_i \right)}=\sum_k^{t-1}{f_k\left( x_i \right)}+f_t\left( x_i \right) y^i(t)=k∑tfk(xi)=k∑t−1fk(xi)+ft(xi)
y ^ i \hat{y}_i y^i 中已经包含了所有树的迭代结果
另一个角度理解
在机器学习中,我们用来衡量模型在未知数据上的准确率的指标,叫做泛化误差(Genelization error)。
一个集成模型(f)在未知数据集(D)上的泛化误差 E(f;D),由方差(var),偏差(bais)和噪声(ε)共同决定,而泛化误差越小,模型就越理想。
从下面的图可以看出来,方差和偏差是此消彼长的,并且模型的复杂度越高,方差越大,偏差越小。
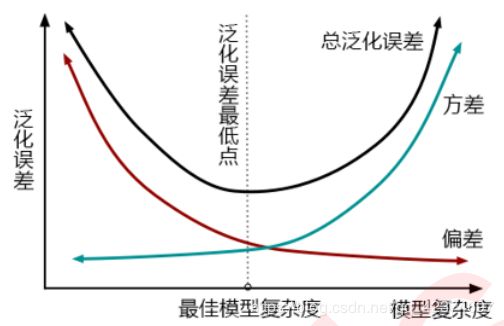
方差可以被简单地解释为模型在不同数据集上表现出来地稳定性,而偏差是模型预测的准确度。那方差-偏差困境就可以对应到 Obj 中了:
O b j = ∑ i = 1 m l ( y i , y ^ i ) + ∑ k = 1 K Ω ( f k ) Obj=\sum_{i=1}^m{l\left( y_i,\hat{y}_i \right)}+\sum_{k=1}^K{\varOmega \left( f_k \right)} Obj=i=1∑ml(yi,y^i)+k=1∑KΩ(fk)
-
第一项是衡量偏差,模型越不准确,偏差就会越大。
-
第二项是衡量方差,模型越复杂,模型的学习就会越具体,到不同数据集上的表现就会差异巨大,方差就会越大。
所以我们求解 Obj 的最小值,其实是在求解方差与偏差的平衡点,以求模型的泛化误差最小,运行速度最快。
我们知道树模型和树的集成模型都是学习天才,是天生过拟合的模型,因此大多数树模型最初都会出现在图像的右上方,我们必须通过剪枝来控制模型不要过拟合。现在XGBoost的损失函数中自带限制方差变大的部分,也就是说XGBoost会比其他的树模型更加聪明,不会轻易落到图像的右上方。
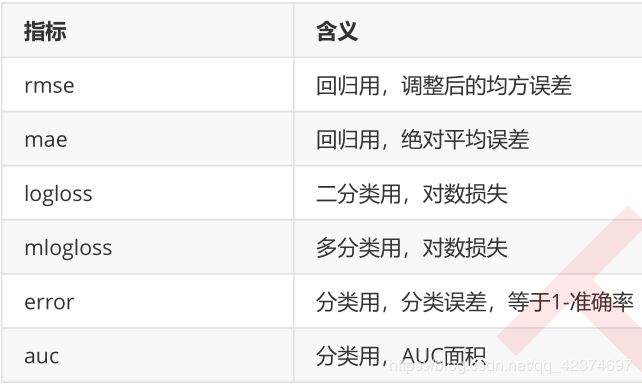
在应用中,使用参数“objective"来确定目标函数的第一部分中的 l ( y i , y ^ i ) l\left( y_i,\hat{y}_i \right) l(yi,y^i),也就是衡量损失的部分。
常用的选择有:

注意:分类型的目标函数导入回归类中会直接报错。
由于xgb中所有的参数都需要自己的输入,并且objective参数的默认值是二分类,因此我们必须手动调节。试试看在其他参数相同的情况下,我们xgboost库本身和sklearn比起来,效果如何:
from xgboost import XGBRegressor as XGBR
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.linear_model import LinearRegression as LinearR
from sklearn.datasets import load_boston
from sklearn.model_selection import KFold, cross_val_score as CVS, train_test_split as TTS
from sklearn.metrics import mean_squared_error as MSE
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
data = load_boston()
#波士顿数据集非常简单,但它所涉及到的问题却很多
X = data.data
y = data.target
Xtrain,Xtest,Ytrain,Ytest = TTS(X,y,test_size=0.3,random_state=420)
# 交叉验证模式 5折 shuffle = True是否打乱数据
cv = KFold(n_splits=5, shuffle = True, random_state=42)
# 在sklean中的调用方法
#默认reg:linear
reg = XGBR(n_estimators=180,random_state=420).fit(Xtrain,Ytrain)
reg.score(Xtest,Ytest) # 0.9050526024842831
MSE(Ytest,reg.predict(Xtest)) # 8.835224213421986
#在xgb实现法
import xgboost as xgb
# 准备数据
#使用类Dmatrix读取数据
dtrain = xgb.DMatrix(Xtrain,Ytrain)
dtest = xgb.DMatrix(Xtest,Ytest)
#非常遗憾无法打开来查看,所以通常都是先读到pandas里面查看之后再放到DMatrix中
dtrain # 看得出来,无论是从 R 2 R^2 R2 还是从MSE的角度来看,都是xgb库本身表现更优秀,这也许是由于底层的代码是由不同团队创造的缘故。
随着样本量的逐渐上升,sklearnAPI中调用的结果与xgboost中直接训练的结果会比较相似,如果希望的话可以分别训练,然后选取泛化误差较小的库。如果可以的话,建议脱离sklearnAPI直接调用xgboost库,因为xgboost库本身的调参要方便许多。
3.3 求解XGB的目标函数
求解目标函数的目的:为了求得在第 t 次迭代中最优的树。
在逻辑回归和支持向量机中,我们通常先将目标函数转化成一种容易求解的方式(比如对偶),然后使用梯度下降或者SMO之类的数学方法来执行最优化过程。
之前我们使用了逻辑回归的迭代过程来帮助大家理解在梯度提升树中树是如何迭代的,那我们是否可以使用逻辑回归的参数求解方式来求解XGB的目标函数呢?
O b j = ∑ i = 1 m l ( y i , y ^ i ) + ∑ k = 1 K Ω ( f k ) Obj=\sum_{i=1}^m{l\left( y_i,\hat{y}_i \right)}+\sum_{k=1}^K{\varOmega \left( f_k \right)} Obj=i=1∑ml(yi,y^i)+k=1∑KΩ(fk)
很遗憾,在XGB中无法使用梯度下降,原因是XGB的损失函数没有需要求解的参数。我们在传统梯度下降中迭代的是参数,而我们在XGB中迭代的是树,树 f k f_k fk 不是数字组成的向量,并且其结构不受到特征矩阵 X 取值大小的直接影响,尽管这个迭代过程可以被类比到梯度下降上,但真实的求解过程却是完全不同。
在求解XGB的目标函数的过程中,我们考虑的是如何能够将目标函数转化成更简单的,与树的结构直接相关的写法,以此来建立树的结构与模型的效果(包括泛化能力与运行速度)之间的直接联系。也因为这种联系的存在,XGB的目标函数又被称为“结构分数”。
y ^ i ( t ) = ∑ k t f k ( x i ) = ∑ k t − 1 f k ( x i ) + f t ( x i ) = y ^ i ( t − 1 ) + f t ( x i ) \hat{y}_{i}^{\left( t \right)}=\sum_k^t{f_k\left( x_i \right)}=\sum_k^{t-1}{f_k\left( x_i \right)}+f_t\left( x_i \right) =\hat{y}_{i}^{\left( t-1 \right)}+f_t\left( x_i \right) y^i(t)=k∑tfk(xi)=k∑t−1fk(xi)+ft(xi)=y^i(t−1)+ft(xi)
首先,我们先来进行第一步转换。
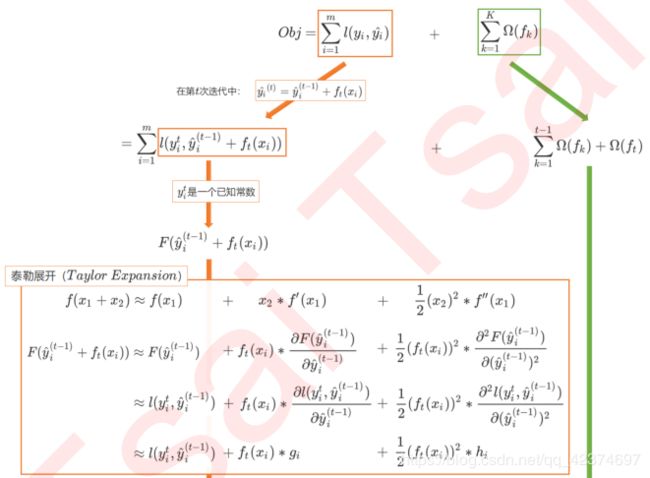

其中 g i g_i gi 和 h i h_i hi 分别是在损失函数 l ( y i t , y ^ i ( t − 1 ) ) l\left( y_i^t,\hat{y}_i^{\left( t-1 \right)} \right) l(yit,y^i(t−1)) 上对 y ^ i ( t − 1 ) \hat{y}_i^{\left( t-1 \right)} y^i(t−1) 所求的一阶导数和二阶导数,他们被统称为每个样本的梯度统计量(gradient statisticts)。
在GBDT和XGB的区别之中,GBDT求一阶导数,XGB求二阶导数,这两个过程根本是不可类比的。XGB在求解极值为目标的求导中也是求解一阶导数。
目标函数可以被顺利转化成:
O b j = ∑ i = 1 m [ f t ( x i ) g i + 1 2 ( f t ( x i ) 2 h i ) ] + Ω ( f t ) Obj=\sum_{i=1}^m{\left[ f_t\left( x_i \right) g_i+\frac{1}{2}\left( f_t\left( x_i \right) ^2h_i \right) \right]}+\varOmega \left( f_t \right) Obj=i=1∑m[ft(xi)gi+21(ft(xi)2hi)]+Ω(ft)
这个式子中, g i g_i gi 和 h i h_i hi 只与传统损失函数相关,核心的部分是需要决定的树 f t f_t ft。接下来,就来研究一下 f t f_t ft 。
3.4 参数化决策树 f k ( x ) f_k\left( x \right) fk(x):参数alpha,lambda
class xgboost.XGBRegressor (
max_depth=3, learning_rate=0.1,
n_estimators=100, silent=True,objective='reg:linear',
booster='gbtree', n_jobs=1, nthread=None,
gamma=0, min_child_weight=1, max_delta_step=0,
subsample=1, colsample_bytree=1, colsample_bylevel=1,
reg_alpha=0,
reg_lambda=1,
scale_pos_weight=1,
base_score=0.5, random_state=0, seed=None,
missing=None, importance_type='gain', **kwargs)
在参数化决策树之前,我们先来简单复习一下回归树的原理。
对于决策树而言,每个被放入模型的任意样本 i 最终一个都会落到一个叶子节点上。对于回归树,通常来说每个叶子节点上的预测值是这个叶子节点上所有样本的标签的均值。
但值得注意的是,XGB作为普通回归树的改进算法,在 上却有所不同。
对于XGB来说,每个叶子节点上会有一个预测分数(prediction score),也被称为叶子权重。这个叶子权重就是所有在这个叶子节点上的样本在这一棵树上的回归取值,用 f k ( x i ) f_k\left( x_i \right) fk(xi) 或者 ω \omega ω 来表示。
一直以来,用 f t 或者 f k f_t\text{或者}f_k ft或者fk代表这棵树,而 f k ( x i ) f_k\left( x_i \right) fk(xi) 表示把样本 x i x_i xi 放入树结构中所获取的叶子权重(分数)
例子
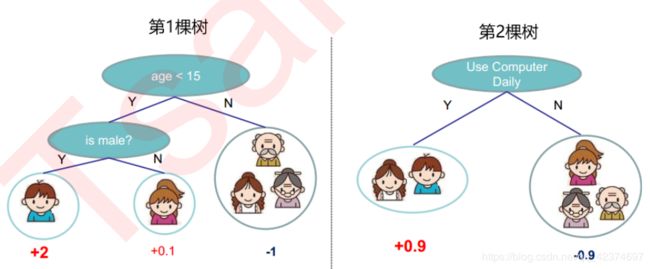
预测一家人对电子游戏的喜好程度,考虑到年轻和年老相比,年轻更可能喜欢电子游戏,以及男性和女性相比,男性更喜欢电子游戏,故先根据年龄大小区分小孩和大人,然后再通过性别区分开是男是女,逐一给各人在电子游戏喜好程度上打分,如下图所示。
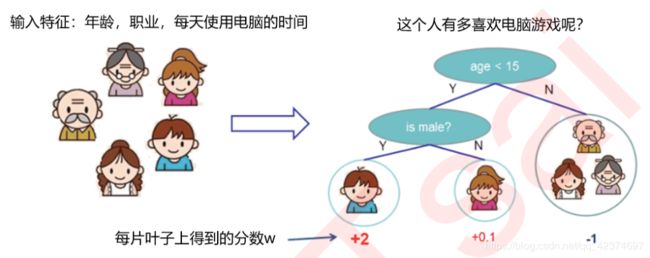
当有多棵树的时候,集成模型的回归结果就是所有树的预测分数之和,假设这个集成模型中总共有 K 棵决策树,则整个模型在这个样本 i 上给出的预测结果为:
y ^ i ( k ) = ∑ k K f k ( x i ) \hat{y}_{i}^{\left( k \right)}=\sum_k^K{f_k\left( x_i \right)} y^i(k)=k∑Kfk(xi)
训练出了2棵树tree1和tree2,两棵树的结论累加起来便是最终的结论,所以
小男孩的预测分数就是两棵树中小男孩所落到的结点的分数相加:2 + 0.9 = 2.9。
爷爷的预测分数同理:-1 + (-0.9)= -1.9
基于这个理解,我们来考虑每一棵树。
对每一棵树,它都有自己独特的结构,这个结构即是指叶子节点的数量,树的深度,叶子的位置等等所形成的一个可以定义唯一模型的树结构。在这个结构中,使用 q ( x i ) q\left( x_i \right) q(xi)表示样本 x i x_i xi 所在的叶子节点,并且使用 ω q ( x i ) \omega _{q\left( x_i \right)} ωq(xi) 来表示这个样本落到第 t 棵树上的第 q ( x i ) q\left( x_i \right) q(xi) 个叶子节点中所获得的分数,于是有:
f t ( x i ) = ω q ( x i ) f_t\left( x_i \right) =\omega _{q\left( x_i \right)} ft(xi)=ωq(xi)
这是对于每一个样本而言的叶子权重,然而在一个叶子节点上的所有样本所对应的叶子权重是相同的。比如,上面的例子
设一棵树上总共包含了 T 个叶子节点,其中每个叶子节点的索引为 j ,则这个叶子节点上的样本权重是 ω j \omega _j ωj。
依据这个,我们定义模型的复杂度 Ω ( f ) \varOmega \left( f \right) Ω(f) 为:
(注意这不是唯一可能的定义)
这个结构中有两部分内容,一部分是控制树结构的 γ T \gamma T γT ,另一部分则是我们的正则项。
叶子数量 T 可以代表整个树结构,这是因为在XGBoost中所有的树都是CART树(二叉树),所以我们可以根据叶子的数量 T 判断出树的深度,而 γ \gamma γ 是自定的控制叶子数量的参数。
至于第二部分正则项,类比一下岭回归和Lasso的结构,参数 α 和 λ \alpha \text{和}\lambda α和λ 的作用其实非常容易理解,他们都是控制正则化强度的参数,可以二选一使用,也可以一起使用加大正则化的力度。当 α 和 λ \alpha \text{和}\lambda α和λ 都为0的时候,目标函数就是普通的梯度提升树的目标函数。
| XGB vs GBDT 核心区别2:正则项的存在 |
|---|
| 在普通的梯度提升树GBDT中,我们是不在目标函数中使用正则项的。但XGB借用正则项来修正树模型天生容易过拟合这个缺陷,在剪枝之前让模型能够尽量不过拟合。(控制过拟合) |
根据以往的经验,往往认为两种正则化达到的效果是相似的,只不过细节不同。比如在逻辑回归当中,两种正则化都会压缩 θ \theta θ 参数的大小,只不过L1正则化会让 θ \theta θ 为0,而L2正则化不会。
在XGB中也是如此。当 α 和 λ \alpha \text{和}\lambda α和λ 越大,惩罚越重,正则项所占的比例就越大,在尽全力最小化目标函数的最优化方向下,叶子节点数量就会被压制,模型的复杂度就越来越低,所以对于天生过拟合的XGB来说,正则化可以一定程度上提升模型效果。
对于两种正则化如何选择的问题,从XGB的默认参数来看,我们优先选择的是L2正则化。当然,如果想尝试L1也不是不可。两种正则项还可以交互,因此这两个参数的使用其实比较复杂。
在实际应用中,正则化参数往往不是我们调参的最优选择,如果真的希望控制模型复杂度,我们会调整 γ \gamma γ 而不是调整这两个正则化参数,因此不必过于在意这两个参数最终如何影响了我们的模型效果。
对于树模型来说,还是剪枝参数地位更高更优先。只需要理解这两个参数从数学层面上如何影响我们的模型就足够了。如果我们希望调整 α 和 λ \alpha \text{和}\lambda α和λ ,我们往往会使用网格搜索来帮助我们。
网格搜索的代码
#使用网格搜索来查找最佳的参数组合
from sklearn.model_selection import GridSearchCV
param = {"reg_alpha":np.arange(0,5,0.05),"reg_lambda":np.arange(0,2,0.05)}
gscv = GridSearchCV(reg,param_grid = param,scoring = "neg_mean_squared_error",cv=cv)
#======【TIME WARNING:10~20 mins】======#
time0=time()
gscv.fit(Xtrain,Ytrain)
print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%S:%f"))
gscv.best_params_
gscv.best_score_
preds = gscv.predict(Xtest)
from sklearn.metrics import r2_score,mean_squared_error as MSE
r2_score(Ytest,preds)
MSE(Ytest,preds)
3.5 寻找最佳树结构:求解 ω \omega ω与T
叶子数量 T
使用 ω q ( x i ) \omega _{q\left( x_i \right)} ωq(xi) 来表示这个样本落到第 t 棵树上的第 q ( x i ) q\left( x_i \right) q(xi) 个叶子节点中所获得的分数
设一棵树上总共包含了 T 个叶子节点,其中每个叶子节点的索引为 j ,则这个叶子节点上的样本权重是 ω j \omega _j ωj
在上一节中,定义了树和树的复杂度的表达式,树使用叶子节点上的预测分数来表达,而树的复杂度则是叶子数目加上正则项:
f t ( x i ) = ω q ( x i ) , Ω ( f t ) = γ T + 1 2 λ ∑ j = 1 T ω j 2 f_t\left( x_i \right) =\omega _{q\left( x_i \right)}\text{,}\varOmega \left( f_t \right) =\gamma T+\frac{1}{2}\lambda \sum_{j=1}^T{\omega _j^2} ft(xi)=ωq(xi),Ω(ft)=γT+21λj=1∑Tωj2
假设现在第 t 棵树的结构已经被确定为 q ,可以将树的结构带入损失函数,来继续转化目标函数。
转化目标函数的目的是:建立树的结构(叶子节点的数量)与目标函数的大小之间的直接联系,以求出在第 t 次迭代中需要求解的最优的树 。
注意,假设使用的是L2正则化(这也是参数lambda和alpha的默认设置,lambda为1,alpha为0),因此接下来的推导也会根据L2正则化来进行。
对于最终的式子,
O b j ( t ) = ∑ j = 1 T [ ω j ∑ i ∈ I j g i + 1 2 ω j 2 ( ∑ i ∈ I j h i + λ ) ] + γ T Obj^{\left( t \right)}=\sum_{j=1}^T{\left[ \omega _j\sum_{i\in I_j}{g_i}+\frac{1}{2}\omega _j^2\left( \sum_{i\in I_j}{h_i+\lambda} \right) \right]}+\gamma T Obj(t)=j=1∑T⎣⎡ωji∈Ij∑gi+21ωj2⎝⎛i∈Ij∑hi+λ⎠⎞⎦⎤+γT
我们定义
G j = ∑ i ∈ I j g i , H j = ∑ i ∈ I j h i G_j=\sum_{i\in I_j}{g_i}\text{,}H_j=\sum_{i\in I_j}{h_i} Gj=i∈Ij∑gi,Hj=i∈Ij∑hi
于是可以有:
O b j ( t ) = ∑ j = 1 T [ ω j G j + 1 2 ω j 2 ( H j + λ ) ] + γ T Obj^{\left( t \right)}=\sum_{j=1}^T{\left[ \omega _jG_j+\frac{1}{2}\omega _j^2\left( H_j+\lambda \right) \right]}+\gamma T Obj(t)=j=1∑T[ωjGj+21ωj2(Hj+λ)]+γT
F ∗ ( ω j ) = ω j G j + 1 2 ω j 2 ( H j + λ ) F^*\left( \omega _j \right) =\omega _jG_j+\frac{1}{2}\omega _j^2\left( H_j+\lambda \right) F∗(ωj)=ωjGj+21ωj2(Hj+λ)
其中每个 j 取值下都是一个以 ω j \omega _j ωj 为自变量的二次函数 ,我们的目标是追求让 Obj 最小,只要单独的每一个叶子 j 取值下的二次函数都最小,那他们的加和必然也会最小。
于是,在 F ∗ F^* F∗ 上对 ω j \omega _j ωj 求导,让一阶导数等于0以求极值,
可得:
样本量 i 已经被归结到了每个叶子当中去,我们的目标函数是基于每个叶子节点,也就是树的结构来计算。所以,目标函数又叫做“结构分数”(structure score),分数越低,树整体的结构越好。如此,就建立了树的结构(叶子)和模型效果的直接联系。
所以在XGB的运行过程中,我们会根据 Obj 的表达式直接探索最好的树结构,也就是说找寻最佳的树。
从式子中可以看出,
λ 和 α \lambda \text{和}\alpha λ和α 是我们设定好的超参数, G j 和 H j G_j\text{和}H_j Gj和Hj 是由损失函数和这个特定结构下树的预测结果 y ^ i ( t − 1 ) \hat{y}_i^{\left( t-1 \right)} y^i(t−1) 共同决定,而 T 只由我们的树结构决定。则我们通过最小化 Obj 所求解出的其实是 T,叶子的数量。
所以本质也就是求解树的结构了。在这个算式下,我们可以有一种思路,那就是枚举所有可能的树结构 q,然后一个个计算 Obj ,待我们选定了最佳的树结构(最佳的 T )之后,我们使用这种树结构下计算出来的 G j 和 H j G_j\text{和}H_j Gj和Hj 就可以求解出每个叶子上的权重 ,如此就找到我们的最佳树结构,完成了这次迭代。
3.6 寻找最佳分枝:结构分数之差
贪婪算法指的是控制局部最优来达到全局最优的算法,决策树算法本身就是一种使用贪婪算法的方法。XGB作为树的集成模型,自然也想到采用这样的方法来进行计算,所以我们认为,如果每片叶子都是最优,则整体生成的树结构就是最优,如此就可以避免去枚举所有可能的树结构。
-
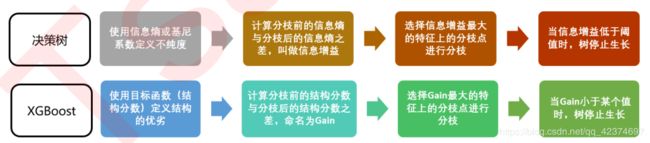
决策树中使用基尼系数或信息熵来衡量分枝之后叶子节点的不纯度,分枝前的信息熵与分枝后的信息熵之差叫做信息增益,信息增益最大的特征上的分枝就被我们选中,当信息增益低于某个阈值时,就让树停止生长。
-
在XGB中,使用的方式是类似的:首先使用目标函数来衡量树的结构的优劣,然后让树从深度0开始生长,每进行一次分枝,我们就计算目标函数减少了多少,当目标函数的降低低于设定的某个阈值时,就让树停止生长。
例子
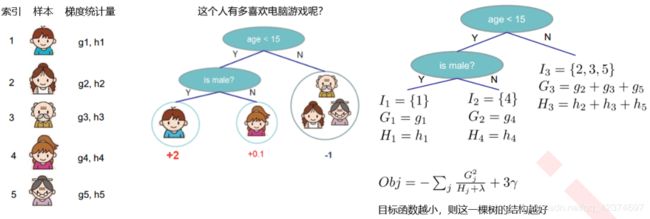
对于中间节点这一个叶子节点而言,T=1 ,则这个节点上的结构分数为:
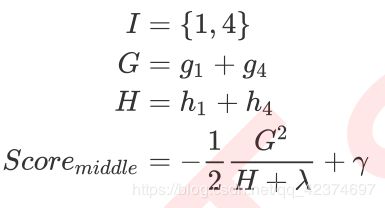
对于弟弟和妹妹节点而言,则有:
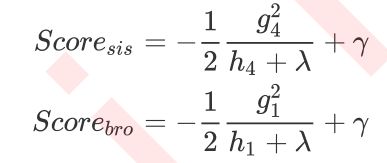
CART树全部是二叉树,因此这个式子是可以推广的。从这个式子我们可以总结出,其实分枝后的结构分数之差为:
其中
G L 和 H L G_L\text{和}H_L GL和HL 从左节点(弟弟节点)上计算得出,
G R 和 H R G_R\text{和}H_R GR和HR 从有节点(妹妹节点)上计算得出,
而
( G L + G R ) \left( G_L+G_R \right) (GL+GR) 和 ( H L + H R ) \left( H_L+H_R \right) (HL+HR)从中间节点上计算得出。对于任意分枝,都可以这样来进行计算。
在现实中,我们会对所有特征的所有分枝点进行如上计算,然后选出让目标函数下降最快的节点来进行分枝。对每一棵树的每一层,我们都进行这样的计算,比起原始的梯度下降,实践证明这样的求解最佳树结构的方法运算更快,并且在大型数据下也能够表现不
错。
3.7 让树停止生长:重要参数gamma
在之前所有的推导过程中,我们都没有提到 γ \gamma γ 这个变量。从目标函数和结构分数之差 G a i n Gain Gain 的式子中来看, γ \gamma γ 是每增加一片叶子就会被剪去的惩罚项。增加的叶子越多,结构分数之差 G a i n Gain Gain 会被惩罚越重,所以 γ \gamma γ 又被称之为是“复杂性控制”(complexity control), γ \gamma γ 是用来防止过拟合的重要参数。
实践证明, γ \gamma γ 是对梯度提升树影响最大的参数之一,其效果丝毫不逊色于n_estimators和防止过拟合的神器max_depth。同时, 还是让树停止生长的重要参数。
在逻辑回归中,我们使用参数 tol 来设定阈值,并规定如果梯度下降时损失函数减小量小于 tol 下降就会停止。
在XGB中,我们规定,只要结构分数之差 G a i n Gain Gain 是大于0的,即只要目标函数还能够继续减小,我们就允许树继续进行分枝。
如此,可以直接通过设定 γ \gamma γ 的大小来让XGB中的树停止生长。
因此 γ \gamma γ 被定义为,在树的叶节点上进行进一步分枝所需的最小目标函数减少量,在决策树和随机森林中也有类似的参数(min_split_loss,min_samples_split)。 设定越大,算法就越保守,树的叶子数量就越少,模型的复杂度就越低。
| 参数含义 | xgb.train() | xgb.XGBRegressor() |
|---|---|---|
| 复杂度的惩罚项 γ \gamma γ | gamma,默认0,取值范围[0, +∞] | gamma,默认0,取值范围[0, +∞] |
如果我们希望从代码中来观察 γ \gamma γ 的作用,使用sklearn中传统的学习曲线等工具就比较困难了。
在sklearn下XGBoost太不稳定,如果这样来调整参数的话,效果就很难保证。因此,为了调整 γ \gamma γ ,引入新的工具,xgboost库中的类xgboost.cv
xgboost.cv (params, dtrain, num_boost_round=10, nfold=3, stratified=False, folds=None, metrics=(), obj=None,
feval=None, maximize=False, early_stopping_rounds=None, fpreproc=None, as_pandas=True, verbose_eval=None,
show_stdv=True, seed=0, callbacks=None, shuffle=True)
import matplotlib.pyplot as plt
from time import time
import datetime
from sklearn.datasets import load_boston
import xgboost as xgb
data = load_boston()
#波士顿数据集非常简单,但它所涉及到的问题却很多
X = data.data
y = data.target
#为了便捷,使用全数据
dfull = xgb.DMatrix(X,y)
#设定参数
param1 = {'silent':True,'obj':'reg:linear',"gamma":0}
num_round = 180 # 迭代次数
n_fold=5 # 5折交叉验证
#使用类xgb.cv
time0 = time()
cvresult1 = xgb.cv(param1, dfull, num_round,n_fold)
print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%S:%f"))
# 00:01:571126
#看看类xgb.cv生成了什么结果?
cvresult1
'''
train-rmse-mean train-rmse-std test-rmse-mean test-rmse-std
0 17.105578 0.129116 17.163215 0.584297
1 12.337973 0.097558 12.519735 0.473457
2 8.994071 0.065756 9.404534 0.472309
3 6.629481 0.050323 7.250335 0.500342
4 4.954406 0.033209 5.920812 0.591874
.. ... ... ... ...
175 0.001299 0.000289 3.669898 0.857676
176 0.001285 0.000261 3.669897 0.857677
177 0.001275 0.000239 3.669903 0.857669
178 0.001263 0.000217 3.669901 0.857672
179 0.001259 0.000208 3.669901 0.857671
[180 rows x 4 columns]
'''
# 180次迭代,可以看出随着树不断增加,模型的效果如何变化
plt.figure(figsize=(20,5))
plt.grid()
plt.plot(range(1,181),cvresult1.iloc[:,0],c="red",label="train,gamma=0")
plt.plot(range(1,181),cvresult1.iloc[:,2],c="orange",label="test,gamma=0")
plt.legend()
plt.show()
xgboost中回归模型的默认模型评估指标是调整后的均方 rmse
也可以换其他的模型评估指标
修改模型评估指标——mae(使用绝对平均误差)
param1 = {'silent':True,'obj':'reg:linear',"gamma":0,"eval_metric":"mae"}
cvresult1 = xgb.cv(param1, dfull, num_round,n_fold)
plt.figure(figsize=(20,5))
plt.grid()
plt.plot(range(1,181),cvresult1.iloc[:,0],c="red",label="train,gamma=0")
plt.plot(range(1,181),cvresult1.iloc[:,2],c="orange",label="test,gamma=0")
plt.legend()
plt.show()
两种模型评估指标都显示出模型存在过拟合
降低过拟合,让两条线越来越接近,一种是让测试集的分数在这里降低;另一种是让训练集的分数上升
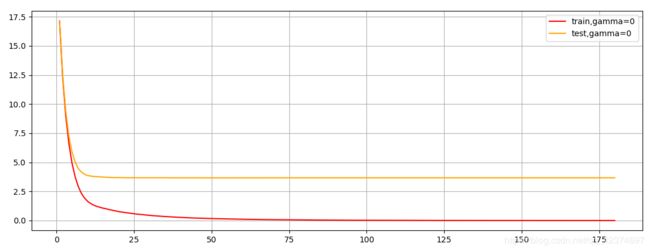
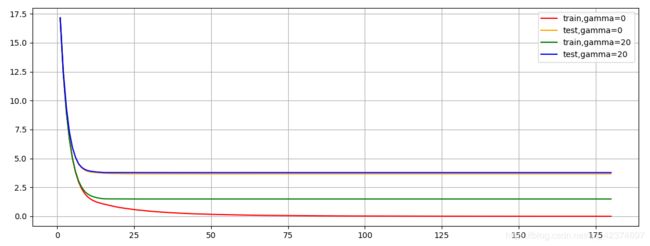
调整 γ \gamma γ
γ \gamma γ=0 和 γ \gamma γ=20
param1 = {'silent':True,'obj':'reg:linear',"gamma":0}
param2 = {'silent':True,'obj':'reg:linear',"gamma":20}
num_round = 180
n_fold=5
time0 = time()
cvresult1 = xgb.cv(param1, dfull, num_round,n_fold)
print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%S:%f"))
time0 = time()
cvresult2 = xgb.cv(param2, dfull, num_round,n_fold)
print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%S:%f"))
plt.figure(figsize=(20,5))
plt.grid()
plt.plot(range(1,181),cvresult1.iloc[:,0],c="red",label="train,gamma=0")
plt.plot(range(1,181),cvresult1.iloc[:,2],c="orange",label="test,gamma=0")
plt.plot(range(1,181),cvresult2.iloc[:,0],c="green",label="train,gamma=20")
plt.plot(range(1,181),cvresult2.iloc[:,2],c="blue",label="test,gamma=20")
plt.legend()
plt.show()
γ \gamma γ=20时确实控制了过拟合问题
γ \gamma γ=0 时和 γ \gamma γ=20 时的测试集分数曲线基本上重叠,但训练集分数曲线却相距较远
也就是说, γ \gamma γ 是通过控制训练集上的训练(降低训练集的表现)来降低过拟合
实际上,决策树中的剪枝参数,但部分都是通过调整我们训练集上的表现(限制训练集上的学习)来控制过拟合
分类的例子(乳腺癌数据集)
from sklearn.datasets import load_breast_cancer
data2 = load_breast_cancer()
x2 = data2.data
y2 = data2.target
dfull2 = xgb.DMatrix(x2,y2)
param1 = {'silent':True,'obj':'binary:logistic',"gamma":0,"nfold":5}
param2 = {'silent':True,'obj':'binary:logistic',"gamma":2,"nfold":5}
num_round = 100
time0 = time()
cvresult1 = xgb.cv(param1, dfull2, num_round,metrics=("error"))
print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%S:%f"))
time0 = time()
cvresult2 = xgb.cv(param2, dfull2, num_round,metrics=("error"))
print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%S:%f"))
plt.figure(figsize=(20,5))
plt.grid()
plt.plot(range(1,101),cvresult1.iloc[:,0],c="red",label="train,gamma=0")
plt.plot(range(1,101),cvresult1.iloc[:,2],c="orange",label="test,gamma=0")
plt.plot(range(1,101),cvresult2.iloc[:,0],c="green",label="train,gamma=2")
plt.plot(range(1,101),cvresult2.iloc[:,2],c="blue",label="test,gamma=2")
plt.legend()
plt.show()
有了xgboost.cv这个工具,我们的参数调整就容易多了。这个工具可以让我们直接看到参数如何影响了模型的泛化能力。接下来,将重点讲解如何使用xgboost.cv这个类进行参数调整。
4 XGBoost应用中的其他问题
4.1 过拟合:剪枝参数与回归模型调参
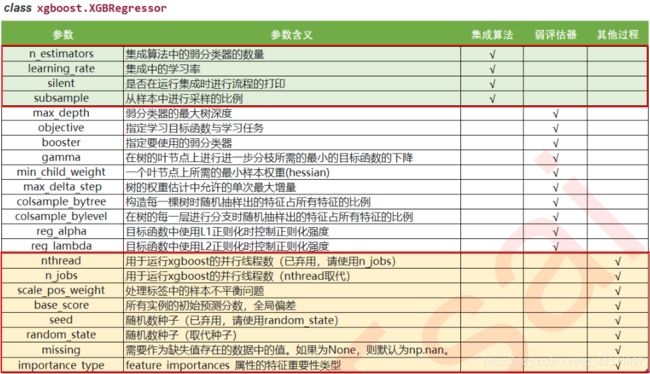
class xgboost.XGBRegressor (max_depth=3, learning_rate=0.1, n_estimators=100, silent=True,
objective='reg:linear', booster='gbtree', n_jobs=1, nthread=None, gamma=0, min_child_weight=1,
max_delta_step=0, subsample=1, colsample_bytree=1, colsample_bylevel=1, reg_alpha=0, reg_lambda=1,
scale_pos_weight=1, base_score=0.5, random_state=0, seed=None, missing=None, importance_type='gain', kwargs)
作为天生过拟合的模型,XGBoost应用的核心之一就是减轻过拟合带来的影响。
作为树模型,减轻过拟合的方式主要是靠对决策树剪枝来降低模型的复杂度,以求降低方差。
在之前的学习中,已经学习了好几个可以用来防止过拟合的参数,包括
- 复杂度控制 γ \gamma γ
- 正则化的两个参数 α 和 λ \alpha \text{和}\lambda α和λ
- 控制迭代速度的参数 η \eta η
- 管理每次迭代前进行的随机有放回抽样的参数 subsample
所有的这些参数都可以用来减轻过拟合。但除此之外,还有几个影响重大的,专用于剪枝的参数:
这些参数中,树的最大深度max_depth是决策树中的剪枝法宝,算是最常用的剪枝参数,不过在XGBoost中,最大深度的功能与参数 γ \gamma γ 相似,因此
- 如果先调节了 γ \gamma γ,则最大深度可能无法展示出巨大的效果。
- 如果先调整了最大深度,则 γ \gamma γ 也有可能无法显示明显的效果。
通常来说,这两个参数中只使用一个,不过两个都试试也没有坏处。
colsample_bytree
colsample_bylevel
colsample_bynode
三个随机抽样特征的参数中,前两个比较常用。在建立树时对特征进行抽样其实是决策树和随机森林中比较常见的一种方法,但是在XGBoost之前,这种方法并没有被使用到boosting算法当中过。
Boosting算法一直以抽取样本(横向抽样)来调整模型过拟合的程度,而实践证明其实纵向抽样(抽取特征)更能够防止过拟合。
参数min_child_weight不太常用,它是一片叶子上的二阶导数 h i h_i hi 之和,当样本所对应的二阶导数很小时,比如说为0.01,min_child_weight若设定为1,则说明一片叶子上至少需要100个样本。
本质上来说,这个参数其实是在控制叶子上所需的最小样本量,因此对于样本量很大的数据会比较有效。如果样本量很小(比如我们现在使用的波士顿房价数据集,则这个参数效用不大)。就剪枝的效果来说,这个参数的功能也被 γ \gamma γ 替代了一部分,通常来说我们会试试看这个参数,但这个参数不是优先选择。
通常当我们获得了一个数据集后,先使用网格搜索找出比较合适的 n_estimators 和 eta 组合,然后使用 γ \gamma γ 或者max_depth观察模型处于什么样的状态(过拟合还是欠拟合,处于方差-偏差图像的左边还是右边?),最后再决定是否要进行剪枝。通常来说,对于XGB模型,大多数时候都是需要剪枝的。
使用 xgb.cv 这个类来进行剪枝调参,以调整出一组泛化能力很强的参数。
import matplotlib.pyplot as plt
from time import time
import datetime
from sklearn.datasets import load_boston
import xgboost as xgb
data = load_boston()
#波士顿数据集非常简单,但它所涉及到的问题却很多
X = data.data
y = data.target
#为了便捷,使用全数据
dfull = xgb.DMatrix(X,y)
#设定参数
param1 = {'silent':True #并非默认
,'obj':'reg:linear' #并非默认
,"subsample":1
,"max_depth":6
,"eta":0.3
,"gamma":0
,"lambda":1
,"alpha":0
,"colsample_bytree":1
,"colsample_bylevel":1
,"colsample_bynode":1
,"nfold":5}
num_round = 200 # 迭代次数 (建立的 树量)
time0 = time()
cvresult1 = xgb.cv(param1, dfull, num_round)
print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%S:%f"))
fig,ax = plt.subplots(1,figsize=(15,10))
#ax.set_ylim(top=5)
ax.grid()
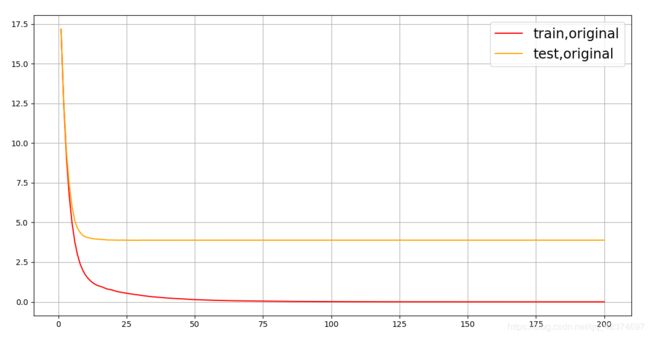
ax.plot(range(1,201),cvresult1.iloc[:,0],c="red",label="train,original")
ax.plot(range(1,201),cvresult1.iloc[:,2],c="orange",label="test,original")
ax.legend(fontsize="xx-large")
plt.show()
从曲线上可以看出,模型现在处于过拟合的状态,要进行剪枝。
我们的目标是:训练集和测试集的结果尽量接近,如果测试集上的结果不能上升,那训练集上的结果降下来也是不错的选择(让模型不那么具体到训练数据,增加泛化能力)。
在这里,我们要使用三组曲线。
一组用于展示原始数据上的结果,
一组用于展示上一个参数调节完毕后的结果,
最后一组用于展示现在我们在调节的参数的结果。
param1 = {'silent':True
,'obj':'reg:linear'
,"subsample":1
,"max_depth":6
,"eta":0.3
,"gamma":0
,"lambda":1
,"alpha":0
,"colsample_bytree":1
,"colsample_bylevel":1
,"colsample_bynode":1
,"nfold":5}
num_round = 200
time0 = time()
cvresult1 = xgb.cv(param1, dfull, num_round)
print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%S:%f"))
fig,ax = plt.subplots(1,figsize=(15,8))
ax.set_ylim(top=5)
ax.grid()
ax.plot(range(1,201),cvresult1.iloc[:,0],c="red",label="train,original")
ax.plot(range(1,201),cvresult1.iloc[:,2],c="orange",label="test,original")
param2 = {'silent':True
,'obj':'reg:linear'
,"max_depth":2
,"eta":0.05
,"gamma":0
,"lambda":1
,"alpha":0
,"colsample_bytree":1
,"colsample_bylevel":0.4
,"colsample_bynode":1
,"nfold":5}
param3 = {'silent':True
,'obj':'reg:linear'
,"subsample":1
,"eta":0.05
,"gamma":20
,"lambda":3.5
,"alpha":0.2
,"max_depth":4
,"colsample_bytree":0.4
,"colsample_bylevel":0.6
,"colsample_bynode":1
,"nfold":5}
time0 = time()
cvresult2 = xgb.cv(param2, dfull, num_round)
print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%S:%f"))
time0 = time()
cvresult3 = xgb.cv(param3, dfull, num_round)
print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%S:%f"))
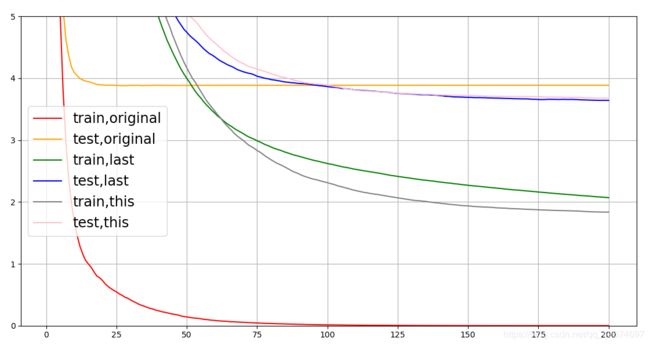
ax.plot(range(1,201),cvresult2.iloc[:,0],c="green",label="train,last")
ax.plot(range(1,201),cvresult2.iloc[:,2],c="blue",label="test,last")
ax.plot(range(1,201),cvresult3.iloc[:,0],c="gray",label="train,this")
ax.plot(range(1,201),cvresult3.iloc[:,2],c="pink",label="test,this")
ax.legend(fontsize="xx-large")
plt.show()
param中的参数取值,需要一步步的调整
1. 一个个参数调整太麻烦,可不可以使用网格搜索呢?
可以!只是使用的时候要注意,首先XGB的参数非常多,参数可取的范围也很广,究竟是使用np.linspace或者np.arange作为参数的备选值也会影响结果,而且网格搜索的运行速度往往不容乐观,因此建议至少先使用xgboost.cv来确认参数的范围,否则很可能花很长的时间做了无用功。
并且,在使用网格搜索的时候,最好不要一次性将所有的参数都放入进行搜索,最多一次两三个。有一些互相影响的参数需要放在一起使用,比如学习率eta和树的数量n_estimators。
另外,如果网格搜索的结果与你的理解相违背,与你手动调参的结果相违背,选择模型效果较好的一个。如果两者效果差不多,那选择相信手动调参的结果。网格毕竟是枚举出结果,很多时候得出的结果可能会是具体到数据的巧合,我们无法去一一解释网格搜索得出的结论为何是这样。如果你感觉都无法解释,那就不要去在意,直接选择结果较好的一个。
2. 调参的时候参数的顺序会影响调参结果吗?
会影响,因此在现实中,我们会优先调整那些对模型影响巨大的参数。在这里,建议的剪枝上的调参顺序是:n_estimators与eta共同调节,gamma或者max_depth,采样和抽样参数(纵向抽样影响更大),最后才是正则化的两个参数。当然,可以根据自己的需求来进行调整。
3. 调参之后测试集上的效果还没有原始设定上的效果好怎么办?
如果调参之后,交叉验证曲线确实显示测试集和训练集上的模型评估效果是更加接近的,推荐使用调参之后的效果。
我们希望增强模型的泛化能力,然而泛化能力的增强并不代表着在新数据集上模型的结果一定优秀,因为未知数据集并非一定符合全数据的分布,在一组未知数据上表现十分优,也不一定就能够在其他的未知数据集上表现优秀。
因此不必过于纠结在现有的测试集上是否表现优秀。当然了,在现有数据上如果能够实现训练集和测试集都非常优秀,那模型的泛化能力自然也会是很强的。
4.2 XGBoost模型的保存和调用
在使用Python进行编程时,我们可能会需要编写较为复杂的程序或者建立复杂的模型。比如XGBoost模型,这个模型的参数复杂繁多,并且调参过程不是太容易,一旦训练完毕,我们往往希望将训练完毕后的模型保存下来,以便日后用于新的数据集。在Python中,保存模型的方法有许多种。我们以XGBoost为例,来讲解两种主要的模型保存和调用方法。
4.2.1 使用Pickle保存和调用模型
pickle是python编程中比较标准的一个保存和调用模型的库,可以使用pickle和open函数的连用,来将我们的模型保存到本地。以刚才我们已经调整好的参数和训练好的模型为例,
我们可以这样来使用pickle:
import pickle
dtrain = xgb.DMatrix(Xtrain,Ytrain)
#设定参数,对模型进行训练
param = {'silent':True
,'obj':'reg:linear'
,"subsample":1
,"eta":0.05
,"gamma":20
,"lambda":3.5
,"alpha":0.2
,"max_depth":4
,"colsample_bytree":0.4
,"colsample_bylevel":0.6
,"colsample_bynode":1}
num_round = 180
bst = xgb.train(param, dtrain, num_round)
#保存模型
pickle.dump(bst, open("xgboostonboston.dat","wb"))
#注意,open中我们往往使用w或者r作为读取的模式,但其实w与r只能用于文本文件 - txt
#当我们希望导入的不是文本文件,而是模型本身的时候,我们使用"wb"和"rb"作为读取的模式
#其中wb表示以二进制写入,rb表示以二进制读入,使用open进行保存的这个文件中是一个可以进行读取或者调用的模型
#看看模型被保存到了哪里?
import sys
sys.path
#导入模型
loaded_model = pickle.load(open("xgboostonboston.dat", "rb"))
print("Loaded model from: xgboostonboston.dat")
#做预测,直接调用接口predict
ypreds = loaded_model.predict(dtest)
from sklearn.metrics import mean_squared_error as MSE, r2_score
MSE(Ytest,ypreds)
r2_score(Ytest,ypreds)
4.2.2 使用Joblib保存和调用模型
Joblib是SciPy生态系统中的一部分,它为Python提供保存和调用管道和对象的功能,处理NumPy结构的数据尤其高效,对于很大的数据集和巨大的模型非常有用。Joblib与pickle API非常相似
dtrain = xgb.DMatrix(Xtrain,Ytrain)
#设定参数,对模型进行训练
param = {'silent':True
,'obj':'reg:linear'
,"subsample":1
,"eta":0.05
,"gamma":20
,"lambda":3.5
,"alpha":0.2
,"max_depth":4
,"colsample_bytree":0.4
,"colsample_bylevel":0.6
,"colsample_bynode":1}
num_round = 180
bst = xgb.train(param, dtrain, num_round)
import joblib
#同样可以看看模型被保存到了哪里
joblib.dump(bst,"xgboost-boston.dat")
# 调用
loaded_model = joblib.load("xgboost-boston.dat")
# 预测
ypreds = loaded_model.predict(dtest)
# 模型评估
MSE(Ytest, ypreds)
r2_score(Ytest,ypreds)
使用sklearn中的模型
from xgboost import XGBRegressor as XGBR
# 训练完毕
bst = XGBR(n_estimators=200,
eta=0.05,
gamma=20,
reg_lambda=3.5,
reg_alpha=0.2,
max_depth=4,
colsample_bytree=0.4,
colsample_bylevel=0.6).fit(Xtrain,Ytrain)
joblib.dump(bst,"xgboost-boston.dat")
loaded_model = joblib.load("xgboost-boston.dat")
#则这里可以直接导入Xtest
ypreds = loaded_model.predict(Xtest)
MSE(Ytest, ypreds)
在这两种保存方法下,我们都可以找到保存下来的dat文件,将这些文件移动到任意计算机上的python下的环境变量路径中(使用sys.path进行查看),则可以使用import来对模型进行调用。注意,模型的保存调用与自写函数的保存调用是两回事,注意区分。
4.3 分类案例:XGB中的样本不均衡问题
一直以回归作为例子,这是由于回归是XGB的常用领域的缘故。然而作为机器学习中的大头,分类算法也是不可忽视的,XGB作为分类的例子自然也是非常多。
存在分类,就会存在样本不平衡问题带来的影响,XGB中存在着调节样本不平衡的参数scale_pos_weight,这个参数非常类似于之前随机森林和支持向量机中都使用到过的class_weight参数,通常在参数中输入的是负样本量与正样本量之比
s u m ( n e g a t i v e i n s tan c e s ) s u m ( p o s i t i v e i n s tan c e s ) \frac{sum\left( negative\ ins\tan ces \right)}{sum\left( positive\ ins\tan ces \right)} sum(positive instances)sum(negative instances)
| 参数含义 | xgb.train() | xgb.XGBClassifier() |
|---|---|---|
| 控制正负样本比例,表示为负/正样本比例在样本不平衡问题中使用 | scale_pos_weight,默认1 | scale_pos_weight,默认1 |
导库,创建样本不均衡的数据集
import numpy as np
import xgboost as xgb
import matplotlib.pyplot as plt
from xgboost import XGBClassifier as XGBC
from sklearn.datasets import make_blobs #自创数据集
from sklearn.model_selection import train_test_split as TTS
# 模型评估指标
# 混淆矩阵
# 召回率
# AUC
from sklearn.metrics import confusion_matrix as cm, recall_score as recall, roc_auc_score as auc
class_1 = 500 #类别1 有500个样本
class_2 = 50 #类别2 只有50个
centers = [[0.0, 0.0], [2.0, 2.0]] #设定两个类别的中心
clusters_std = [1.5, 0.5] #设定两个类别的方差,通常来说,样本量比较大的类别会更加松散
X, y = make_blobs(n_samples=[class_1, class_2],
centers=centers,
cluster_std=clusters_std,
random_state=0, shuffle=False)
X.shape # (550, 2)
X
'''
array([[ 2.64607852, 0.60023581],
[ 1.46810698, 3.3613398 ],
[ 2.80133699, -1.46591682],
...,
[ 3.07478727, 1.95487808],
[ 2.36582946, 1.96725581],
[ 2.17408462, 2.33162904]])
'''
y.shape # (550,)
'''
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
..........
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])
'''
Xtrain, Xtest, Ytrain, Ytest = TTS(X,y,test_size=0.3,random_state=420)
(y == 1).sum() / y.shape[0] # 0.09090909090909091
在数据集上建模:sklearn模式
# 分类模型
clf = XGBC().fit(Xtrain,Ytrain)
ypred = clf.predict(Xtest)
'''
array([0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0,
1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1])
'''
# 准确率
clf.score(Xtest,Ytest) # 0.9272727272727272
cm(Ytest,ypred,labels=[1,0]) # 混淆举证 少数类写在前面
# 1 有九个少数类被分正确,四个分错误
# 0 有144个多数类被分正确,8个错误
'''
array([[ 9, 4],
[ 8, 144]], dtype=int64)
'''
# 召回率
recall(Ytest,ypred) # 0.6923076923076923
# AUC
auc(Ytest,clf.predict_proba(Xtest)[:,1]) # 0.9701417004048585
#负/正样本比例
# 现在
# 多数类是500个
# 少数类是50个
# 所以 500/50=10 scale_pos_weight
clf_ = XGBC(scale_pos_weight=10).fit(Xtrain,Ytrain)
ypred_ = clf_.predict(Xtest)
clf_.score(Xtest,Ytest) # 0.9333333333333333
# 混淆矩阵
cm(Ytest,ypred_,labels=[1,0])
# 少数类被分正确比上次好一点点
'''
array([[ 10, 3],
[ 8, 144]], dtype=int64)
'''
recall(Ytest,ypred_) # 0.7692307692307693
auc(Ytest,clf_.predict_proba(Xtest)[:,1]) # 0.9686234817813765
随着样本权重逐渐增加,模型的recall,auc和准确率如何变化?
for i in [1,5,10,20,30]:
clf_ = XGBC(scale_pos_weight=i).fit(Xtrain,Ytrain)
ypred_ = clf_.predict(Xtest)
print(i)
print("\tAccuracy:{}".format(clf_.score(Xtest,Ytest)))
print("\tRecall:{}".format(recall(Ytest,ypred_)))
print("\tAUC:{}".format(auc(Ytest,clf_.predict_proba(Xtest)[:,1])))
'''
1
Accuracy:0.9272727272727272
Recall:0.6923076923076923
AUC:0.9701417004048585
5
Accuracy:0.9393939393939394
Recall:0.8461538461538461
AUC:0.9660931174089069
10
Accuracy:0.9333333333333333
Recall:0.7692307692307693
AUC:0.9696356275303644
20
Accuracy:0.9333333333333333
Recall:0.7692307692307693
AUC:0.9686234817813765
30
Accuracy:0.9393939393939394
Recall:0.8461538461538461
AUC:0.9701417004048583
'''
在数据集上建模:xgboost模式
# 数据转换
dtrain = xgb.DMatrix(Xtrain,Ytrain)
dtest = xgb.DMatrix(Xtest,Ytest)
#看看xgboost库自带的predict接口
# 参数设置
param= {'silent':True,
'objective':'binary:logistic',
"eta":0.1,
"scale_pos_weight":1}
num_round = 100 # 迭代次数
bst = xgb.train(param, dtrain, num_round)
preds = bst.predict(dtest) # 返回概率 每一个样本所对应的分类概率
'''
array([0.00110357, 0.00761518, 0.00110357, 0.00110357, 0.93531454,
0.00466839, 0.00110357, 0.00110357, 0.00110357, 0.00110357,
....
0.00110357, 0.00110357, 0.92388713, 0.90231985, 0.80084217],
dtype=float32)
'''
#自己设定阈值
ypred = preds.copy()
ypred[preds > 0.5] = 1 # 概率大于0.5的分为1类
ypred[ypred != 1] = 0
ypred
'''
array([0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
...
1., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 1., 1.], dtype=float32)
'''
#写明参数
scale_pos_weight = [1,5,10]
names = ["negative vs positive: 1"
,"negative vs positive: 5"
,"negative vs positive: 10"]
[*zip(names,scale_pos_weight)]
'''
[('negative vs positive: 1', 1),
('negative vs positive: 5', 5),
('negative vs positive: 10', 10)]
'''
#导入模型评估指标
from sklearn.metrics import accuracy_score as accuracy, recall_score as recall, roc_auc_score as auc
for name,i in zip(names,scale_pos_weight):
param = {'silent':True,
'objective':'binary:logistic',
"eta":0.1,
"scale_pos_weight":i}
num_round = 100
clf = xgb.train(param, dtrain, num_round)
preds = clf.predict(dtest)
ypred = preds.copy()
ypred[preds > 0.5] = 1
ypred[ypred != 1] = 0
print(name)
print("\tAccuracy:{}".format(accuracy(Ytest,ypred)))
print("\tRecall:{}".format(recall(Ytest,ypred)))
print("\tAUC:{}".format(auc(Ytest,preds)))
'''
negative vs positive: 1
Accuracy:0.9272727272727272
Recall:0.6923076923076923
AUC:0.9741902834008097
negative vs positive: 5
Accuracy:0.9393939393939394
Recall:0.8461538461538461
AUC:0.9635627530364372
negative vs positive: 10
Accuracy:0.9515151515151515
Recall:1.0
AUC:0.9665991902834008
'''
#当然我们也可以尝试不同的阈值
# 双重循环
for name,i in zip(names,scale_pos_weight):
for thres in [0.3,0.5,0.7,0.9]:
param= {'silent':True,
'objective':'binary:logistic',
"eta":0.1,
"scale_pos_weight":i}
clf = xgb.train(param, dtrain, num_round)
preds = clf.predict(dtest)
ypred = preds.copy()
ypred[preds > thres] = 1 # 不同阈值 不同scale_pos_weight下的结果
ypred[ypred != 1] = 0
print("{},thresholds:{}".format(name,thres))
print("\tAccuracy:{}".format(accuracy(Ytest,ypred)))
print("\tRecall:{}".format(recall(Ytest,ypred)))
print("\tAUC:{}".format(auc(Ytest,preds)))
'''
negative vs positive: 1,thresholds:0.3
Accuracy:0.9393939393939394
Recall:0.8461538461538461
AUC:0.9741902834008097
negative vs positive: 1,thresholds:0.5
Accuracy:0.9272727272727272
Recall:0.6923076923076923
AUC:0.9741902834008097
negative vs positive: 1,thresholds:0.7
Accuracy:0.9212121212121213
Recall:0.6153846153846154
AUC:0.9741902834008097
negative vs positive: 1,thresholds:0.9
Accuracy:0.9515151515151515
Recall:0.5384615384615384
AUC:0.9741902834008097
在 scale_pos_weight为1的情况下,调节阈值无法改变AUC ,但是可以调整召回率和准确率
negative vs positive: 5,thresholds:0.3
Accuracy:0.9515151515151515
Recall:1.0
AUC:0.9635627530364372
negative vs positive: 5,thresholds:0.5
Accuracy:0.9393939393939394
Recall:0.8461538461538461
AUC:0.9635627530364372
negative vs positive: 5,thresholds:0.7
Accuracy:0.9272727272727272
Recall:0.6923076923076923
AUC:0.9635627530364372
negative vs positive: 5,thresholds:0.9
Accuracy:0.9212121212121213
Recall:0.6153846153846154
AUC:0.9635627530364372
在 scale_pos_weight为5的情况下,调节阈值无法改变AUC
negative vs positive: 10,thresholds:0.3
Accuracy:0.9515151515151515
Recall:1.0
AUC:0.9665991902834008
negative vs positive: 10,thresholds:0.5
Accuracy:0.9515151515151515
Recall:1.0
AUC:0.9665991902834008
negative vs positive: 10,thresholds:0.7
Accuracy:0.9393939393939394
Recall:0.8461538461538461
AUC:0.9665991902834008
negative vs positive: 10,thresholds:0.9
Accuracy:0.9212121212121213
Recall:0.6153846153846154
AUC:0.9665991902834008
'''
实际上,建议只调整一个
可以看出,在xgboost库和sklearnAPI中,参数scale_pos_weight都非常有效。
本质上来说,scale_pos_weight参数是通过调节预测的概率值来调节,可以通过查看bst.predict(Xtest)返回的结果来观察概率受到了怎样的影响。
因此,当我们只关心预测出的结果是否准确,AUC面积或者召回率是否足够好,我们就可以使用scale_pos_weight参数来帮助我们。
4.4 XGBoost类中的其他参数和功能
到目前为止,已经了解XGBoost类中的大部分参数和功能。
这些参数和功能主要覆盖了XGBoost中的梯度提升树的原理以及XGBoost自身所带的一-些特性。还有一些其他的参数和用法,是算法实际应用时需要考虑的问题。
- 更多计算资源:n_jobs
nthread和n_jobs都是算法运行所使用的线程,与sklearn中规则一样,输入整数表示使用的线程,输入-1表示使用计算机全部的计算资源。如果数据量很大,则可能需要这个参数来为我们调用更多线程。
- 降低学习难度:base_score
base_score是一个比较容易被混淆的参数,它被叫做全局偏差,在分类问题中,它是我们希望关注的分类的先验概率。比如说,如果我们有1000个样本,其中300个正样本,700个负样本,则base_score就是0.3。
对于回归来说,这个分数默认0.5,但其实这个分数在这种情况下并不有效。许多使用XGBoost的人已经提出,当使用回归的时候base_score的默认应该是标签的均值,不过现在xgboost库尚未对此做出改进。使用这个参数,我们便是在告诉模型一些我们了解但模型不一定能够从数据中学习到的信息。通常我们不会使用这个参数,但对于严重的样本不均衡问题,设置一个正确的base_score取值是很有必要的。
- 生成树的随机模式:random_state
在xgb库和sklearn中,都存在空值生成树的随机模式的参数random_state。在之前的剪枝中,我们提到可以通过随机抽样样本,随机抽样特征来减轻过拟合的影响,我们可以通过其他参数来影响随机抽样的比例,却无法对随机抽样干涉更多,因此,真正的随机性还是由模型自己生成的。如果希望控制这种随机性,可以在random_state参数中输入固定整数。需要注意的是,xgb库和sklearn库中,在random_state参数中输入同一个整数未必表示同一个随机模式,不一定会得到相同的结果,因此导致模型的feature_importances也会不一致。
- 自动处理缺失值:missing
XGBoost被设计成是能够自动处理缺失值的模型,这个设计的初衷其实是为了让XGBoost能够处理稀疏矩阵。我们可以在参数missing中输入一个对象,比如np.nan,或数据的任意取值,表示将所有含有这个对象的数据作为空值处理。XGBoost会将所有的空值当作稀疏矩阵中的0来进行处理,因此在使用XGBoost的时候,我们也可以不处理缺失值。当然,通常来说,如果我们了解业务并且了解缺失值的来源,我们还是希望手动填补缺失值。