吴恩达机器学习笔记---正规方程及推导
前言
1.正规方程(Normal Equation)
2.正规方程不可逆性及其推导过程
正规方程(Normal Equation)
到目前为止,对模型参数 θ 0 \theta_{0} θ0, θ 1 \theta_{1} θ1, θ 2 \theta_{2} θ2… θ n \theta_{n} θn的求解都是使用梯度下降的方式,这种迭代算法需要经过很多次迭代才能收敛到全局最小值。而我们知道求解函数取最小值时候的解可以利用求导,并令倒数为0取得(这个说法对一般的函数来说不准确,但对线性模型,代价函数是凸函数,是完全正确的)。正规方程正是提供了这样一种解析算法,与其使用迭代算法 我们可以直接一次性求解 θ \theta θ的最优值。
直接给出正规方程的公式:
θ = ( X T X ) − 1 X T y \theta ={{\left( {X^T}X \right)}^{-1}}{X^{T}}y θ=(XTX)−1XTy
式子中, X X X为特征矩阵,也就是特征变量 x 0 x_{0} x0, x 1 x_{1} x1… x n x_{n} xn的集合,例如:
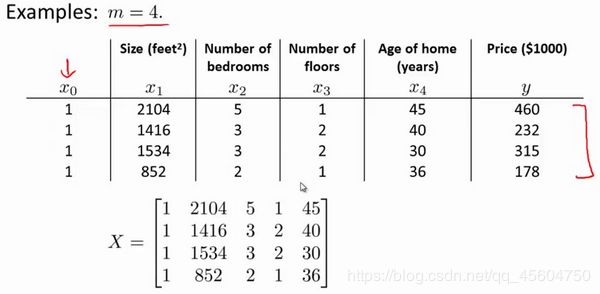
y y y为输出变量,即标签,在上例中, y = [ 460 232 315 178 ] y\text{=}\begin{bmatrix} 460\\ 232\\ 315\\ 178 \end{bmatrix} y=⎣⎢⎢⎡460232315178⎦⎥⎥⎤。说明一下,正规方程不需要对特征进行缩放或者归一化操作。这时,我们可以直接利用公式对 θ \theta θ进行求解:
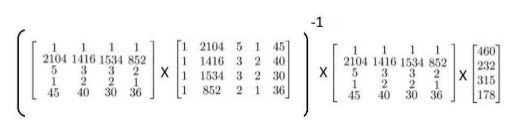
下面比较正规方程和梯度下降的区别,便于我们确定何时使用梯度下降,何时使用正规方程。
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择学习率 α \alpha α | 不需要 |
| 需要多次迭代 | 一次运算得出 |
| 当特征数量 n n n大时也能较好适用 | 需要计算 ( X T X ) − 1 {{\left( {{X}^{T}}X \right)}^{-1}} (XTX)−1 如果特征数量n较大则运算代价大,因为矩阵逆的计算时间复杂度为 O ( n 3 ) O\left( {{n}^{3}} \right) O(n3),通常来说当 n n n小于10000 时还是可以接受的 |
| 适用于各种类型的模型 | 只适用于线性模型,不适合逻辑回归模型等其他模型 |
正规方程的公式是这样的: θ = ( X T X ) − 1 X T y \theta ={{\left( {X^T}X \right)}^{-1}}{X^{T}}y θ=(XTX)−1XTy,我们不难发现,如果特征矩阵 X X X不可逆,也就是没有逆矩阵,我们怎么使用正规方程求解。我们要先找到矩阵不可逆的原因。
-
矩阵中存在线性相关的特征
例如, x 1 {x_{1}} x1是以英尺为尺寸规格计算的房子, x 2 {x_{2}} x2是以平方米为尺寸规格计算的房子,同时,你也知道1米等于3.28英尺,这样,你的这两个特征值将始终满足约束: x 1 = x 2 ∗ ( 3.28 ) 2 {x_{1}}={x_{2}}*{{\left( 3.28 \right)}^{2}} x1=x2∗(3.28)2,对于这样的,我们称 x 1 {x_{1}} x1, x 2 {x_{2}} x2线性相关,矩阵不可逆。 -
特征数量大于样本数量
例如,有 m m m等于10个的训练样本,也有 n n n等于100的特征数量,我们尝试从10个训练样本中找到满足101个参数的值,这也会导致矩阵的不可逆。
所以,在发现矩阵不可逆的时候,可以通过检查是否有多余的特征,即线性相关的特征,删除其中一个就好;或者如果是特征数量过多,就删除一些特征。除此之外,还可以使用pinv()函数来求取伪逆。总之,发生不可逆的情况非常少,我们不要过多地关注。
以下是正规方程的推导过程:
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J\left( \theta \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( {h_{\theta}}\left( {x^{(i)}} \right)-{y^{(i)}} \right)}^{2}}} J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2
其中: h θ ( x ) = θ T X = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n {h_{\theta}}\left( x \right)={\theta^{T}}X={\theta_{0}}{x_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}} hθ(x)=θTX=θ0x0+θ1x1+θ2x2+...+θnxn
将向量表达形式转为矩阵表达形式,则有 J ( θ ) = 1 2 m ( X θ − y ) 2 J(\theta )=\frac{1}{2m}{{\left( X\theta -y\right)}^{2}} J(θ)=2m1(Xθ−y)2 ,其中 X X X为 m m m行 n + 1 n+1 n+1列的矩阵( m m m为样本个数, n + 1 n+1 n+1为特征个数), θ \theta θ为 n + 1 n+1 n+1行1列的矩阵, y y y为 m m m行1列的矩阵,对 J ( θ ) J(\theta ) J(θ)进行如下变换
J ( θ ) = 1 2 ( X θ − y ) T ( X θ − y ) J(\theta )=\frac{1}{2}{{\left( X\theta -y\right)}^{T}}\left( X\theta -y \right) J(θ)=21(Xθ−y)T(Xθ−y)
= 1 2 ( θ T X T − y T ) ( X θ − y ) =\frac{1}{2}\left( {{\theta }^{T}}{{X}^{T}}-{{y}^{T}} \right)\left(X\theta -y \right) =21(θTXT−yT)(Xθ−y)
= 1 2 ( θ T X T X θ − θ T X T y − y T X θ − y T y ) =\frac{1}{2}\left( {{\theta }^{T}}{{X}^{T}}X\theta -{{\theta}^{T}}{{X}^{T}}y-{{y}^{T}}X\theta -{{y}^{T}}y \right) =21(θTXTXθ−θTXTy−yTXθ−yTy)
接下来对 J ( θ ) J(\theta ) J(θ)偏导,需要用到以下几个矩阵的求导法则:
d A B d B = A T \frac{dAB}{dB}={{A}^{T}} dBdAB=AT
d X T A X d X = 2 A X \frac{d{{X}^{T}}AX}{dX}=2AX dXdXTAX=2AX
所以有:
∂ J ( θ ) ∂ θ = 1 2 ( 2 X T X θ − X T y − ( y T X ) T − 0 ) \frac{\partial J\left( \theta \right)}{\partial \theta }=\frac{1}{2}\left(2{{X}^{T}}X\theta -{{X}^{T}}y -{}({{y}^{T}}X )^{T}-0 \right) ∂θ∂J(θ)=21(2XTXθ−XTy−(yTX)T−0)
= 1 2 ( 2 X T X θ − X T y − X T y − 0 ) =\frac{1}{2}\left(2{{X}^{T}}X\theta -{{X}^{T}}y -{{X}^{T}}y -0 \right) =21(2XTXθ−XTy−XTy−0)
= X T X θ − X T y ={{X}^{T}}X\theta -{{X}^{T}}y =XTXθ−XTy
令 ∂ J ( θ ) ∂ θ = 0 \frac{\partial J\left( \theta \right)}{\partial \theta }=0 ∂θ∂J(θ)=0,
则有 θ = ( X T X ) − 1 X T y \theta ={{\left( {X^{T}}X \right)}^{-1}}{X^{T}}y θ=(XTX)−1XTy