jpeg编码学习笔记
jpeg编码学习笔记
各种图片格式目的是在网络传输和存储的时候使用更少的字节,即起到压缩的作用。在图片格式解码后,无论图片的格式,图片数据都是像素数组。
本文将尝试通过JPEG这种图片编码格式的学习,了解图片编码的秘密。
JPEG简介
一张100X100大小的普通图片,如果未经压缩,大概在100*100*4*8bits=0.3MB左右,这也是图片在内存中占用的内存大小。
通常JPEG文件相对于原始图像,能够得到1/8的压缩比,如此高的压缩率是如何做到的呢?
JPEG能够获得如此高的压缩比是因为使用了有损压缩技术,所谓有损压缩,就是把原始数据中不重要的部分去掉,以便可以用更小的体积保存。
JPEG编码是基于两个idea,第一个是基于相邻的像素信息是相近的,即空间冗余性,尽量少记录重复的数据来达到压缩的效果。第二个是基于图像信号的频谱特性,图像包含各种频率,大部分为低频频谱,少部分为高频频谱。可以保留包含图像信息较多的低频频谱,舍去包含图像信息较少的高频频谱。而达到图片质量没有可察觉的损伤,又能达到压缩的效果。这也说明了JPEG是有损编码。
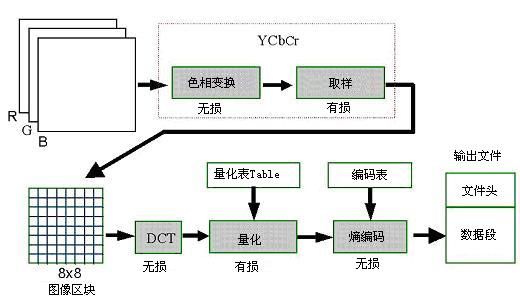
JPEG的编码过程
1.色彩空间转换
将RGB色彩空间转换到其他色彩空间,比如YUV色彩空间。
出现YUV,主要有两个原因,一个是为了让彩色信号兼容黑白电视机,另外一个原因是为了减少传输的带宽。
下图为老电视后面的色差接口。

YUV中,Y表示亮度,U和V表示色度,总之它是将RGB信号进行了一种处理,根据人对亮度更敏感些,增加亮度的信号,减少颜色的信号,以这样“欺骗”人的眼睛的手段来节省空间。YUV的格式也很多,不过常见的就是422和420格式。
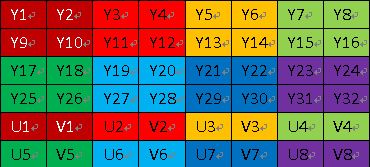
下图为420格式,每四个Y共用一组UV分量,每个YUV分量和RGB一样都用8位来表示,YUV色彩空间就比RGB色彩空间所需的存储空间少一半,数据就被压缩到了一半。
2.离散余弦变换DCT
简单地说,DCT是傅里叶变换的一种,变换后会得到一个系数。
有关DCT的详细介绍可以看这个视频。
在JPEG压缩过程中,经过颜色空间的转换,每一个色值表示成8X8的图像块,下图为一个色彩域取样块,转化为频率域的DCT系数块:

图片经过此步骤会输出一个频率系数矩阵,左上的系数幅度值最大,越往右下,系数的幅度值越小,频率越高。大部分图片信息都在频率域矩阵左上区域,右下几乎不含有图片信息,甚至只含杂波。
注意:转换后的DCT系数块矩阵(x,y)处的值并不和转换前的颜色空间矩阵(x,y)处的像素值直接对应。
这一步骤没有压缩作用,它目的是为下一步骤找低频和高频区域,也就是找出留下的区域和舍去的区域。
3.量化
此步是将上步求得的DCT系数的简化的过程,利用人眼对高频部分不敏感的特性来舍去高频部分。
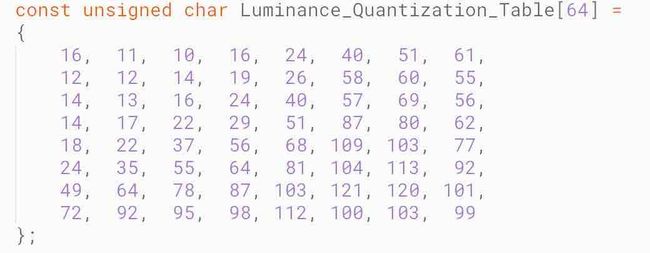
这里有两张表分别对亮度和色度做量化处理。
量化表是控制 JPEG 压缩比的关键。
DCT系数矩阵中的不同位置的值代表了图像数据中不同频率的分量,这两张表中的数据是根据人眼对不同频率的敏感程度的差别所积累下的经验制定的。这个步骤除掉了一些高频量, 损失了很多细节。
但事实上人眼对高空间频率远没有低频敏感.所以处理后的视觉损失很小。
另一个重要原因是所有的图片的点与点之间会有一个色彩过渡的过程。大量的图象信息被包含在低空间频率中。 经过量化处理后, 在高空间频率段, 将出现大量连续的零。
把上面的DCT系数块通过量化后的结果如下图,其中第一个数-26是直流DC部分,它是一块图象样本的平均值,包含了原始8x8图像块中的很多能量,其余的是交流AC部分。
计算方法为:频率系数矩阵的数值除以对应量化表位置上的数值,并四舍五入到最近的整数。

解码的时候,反量化步骤会乘回量化表相应值,但是四舍五入导致低频有所损失,高频0字段被舍弃。此步为有损运算,会导致图像质量变低。所以说JPEG是有损编码。
4.zig-zag游程编码
量化后的数据还可以进行简化,更大程度的去压缩。

根据上面的zig-zag表重排数据的过程:

根据ZigZag表的规则对量化后的数据进行重排后的结果中可以看到出现连续的多个0,这样有利于进行游程编码。
5.范式Huffman编码
基本原理
huffman编码的基本原理是根据数据中元素的使用频率,调整元素的编码长度,以得到更高的压缩比。
举个例子,比如下面这段数据
AABCBABBCDBBDDBAABDBBDABBBBDDEDBD
这段数据里面包含了33个字符,每种字符出现的次数统计如下
| 字符 | A | B | C | D | E |
| 次数 | 6 | 15 | 2 | 9 | 1 |
如果我们用我们常见的定长编码,因为有5个文字,可以用3个bit表示,那么这段文字共需要3*33 = 99个bit来保存
| 字符 | A | B | C | D | E |
| 编码 | 001 | 010 | 011 | 100 | 101 |
如果根据字符出现的概率,使用如下的编码
| 字符 | A | B | C | D | E |
| 编码 | 100 | 0 | 1110 | 10 | 1111 |
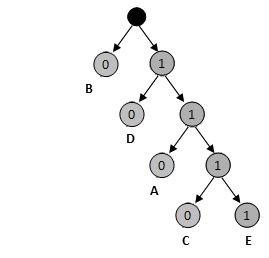
那么这段文字共需要3x6 + 1x15 + 4x2 + 2x9 + 4x1 = 63bit,压缩比为63%。 是较短的编码不能够是较长编码的前缀,比如上面这个编码,就是由下面的这颗二叉树生成的。
哈弗曼编码一般都是使用二叉树来生成的,频率会高的数据对应的树节点的位置越高。这样得到的编码符合前缀规则,也就是较短的编码不能够是较长编码的前缀。
Huffman编码在JPEG中
假设在JPEG量化处理后的数据为:
35,7,0,0,0,-6,-2,0,0,-9,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,8,0,0,0,…,0
根据RLE编码(游程编码)规则
1、用固定的4位来存储重复的数量,所以最多重复内容可以记录数量为15,超过15次要进行分段处理;
2、只将0作为重复的内容,每个数值记录前面有多少重复的0,末尾如果都是0用EOB作为代表;
3、此步不包含第一个数值,第一个数为直流系数,此步只处理交流系数。
得到处理结果:
为了提高储存效率, JPEG 里并不直接保存数值, 而是将数值按位数分成 16 组,JPEG提供了一张标准的码表用于对这些数字编码

举例来说,第3个单元中的“-6”这个数字,在表中的位置是长度为3的那组,所对应的bit码是“001”,由于这种编码附带长度信息,所以我们的数据变成了如下的格式。

对于括号前面的数字的编码,分成DC编码和AC编码。
下表是针对直流(DC)部分即第一个数字的哈弗曼表,由于直流部分没有前置的0,所以取值范围在0~15之间。
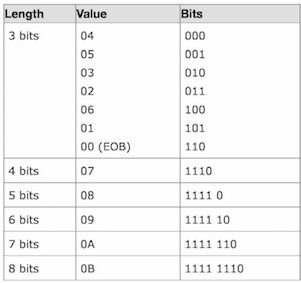
对于其余的交流(AC)部分,取值范围在0~255,哈夫曼表如下:
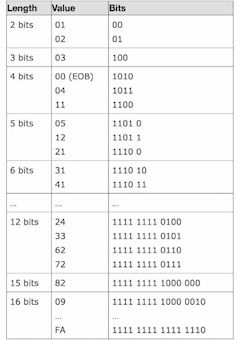
完整个编码过程如下表,最终的数据使用10个字节保存了原本长度为64字节的数据,JPEG的压缩算法完成。

参考
- http://blog.mrriddler.com/2016/07/20/%E5%9B%BE%E7%89%87%E4%B9%8B%E6%97%85/
- http://thecodeway.com/blog/?p=69
- http://www.impulseadventure.com/photo/jpeg-huffman-coding.html
- 《数字图像处理编程入门》
- http://www.ibm.com/developerworks/cn/linux/l-cn-jpeg/index.html