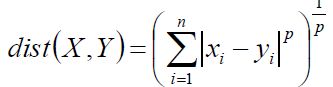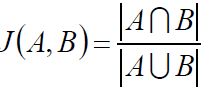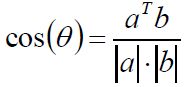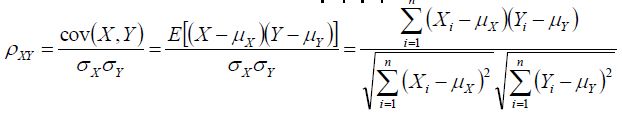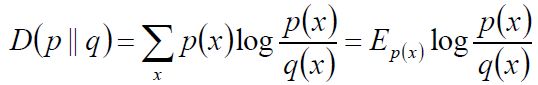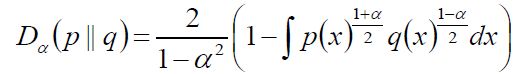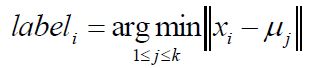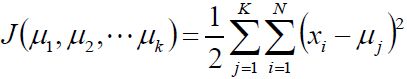聚类之K-means

注：本文中所有公式和思路来自于邹博先生的《机器学习升级版》，我只是为了加深记忆和理解写的本文。

聚类是典型的无监督学习，聚类本质就是对大量的未知标记的数据集，按照数据内在的相似性将数据集划分为多个类别，使类别内的数据相似性较大，而类别间的相似度较小。

本文将会介绍K-means算法以及改进。

那么我们怎么来衡量数据见的相似度呢？

闵可夫斯基距离Minkowski/欧氏距离：

如果p取2的话就是欧氏距离，如果p取1的话就是曼哈顿距离。

杰卡德相似系数(Jaccard):

Jaccard相关系数在推荐系统中应用很多，比如评价两个用户之间喜好的相似度。

余弦相似度(cosine similarity)：

夹角余弦在文本发现、推荐系统中用的比较多。

Pearson相关系数：

相对熵(KL散度)：

Hellinger距离：

KL散度和Hellinger距离联系很大，当α等于0可以相互推导出来。

其实这些距离度量公式之间往往都是有联系，夹角余弦和Pearson相关系数也是可以通过平移和求协方差得到。

K-means

我们首先给定一个有N个实例的数据集，构造数据的K个簇，k≤n，满足以下条件：

(1)： 每个簇至少包含一个一个对象。

(2)： 每个对象只属于一个簇

(3)： 将满足上诉条件的k个簇称作一个合理的划分

基本思路：对于给定的类别数目k，首先给出初始划分，通过迭代改变样本和簇的隶属关系，使得每一次改进后的划分都比上一次要好。

算法：

输入：样本S = x1,x2...xm，k(聚类中心的个数)

输出：每个样本被标记为某类

(1)：初始随机选择k个聚类中心μ1，μ2... μk

(2)：对于每个样本xi，将其标记为距离类别中心最近的类别：

(3)：将每个聚类中心更新为隶属于该类别的所有样本的均值：

(4)：重复(2)(3)两步直到类别中心的变化小于阈值

终止条件可以选择多种方式：

迭代次数/簇中心变化率/最小平方误差MSE(Minimum Squared Error)

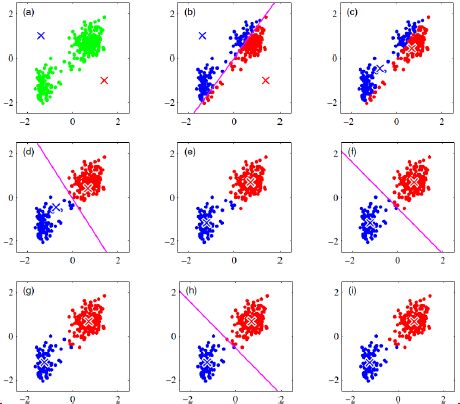
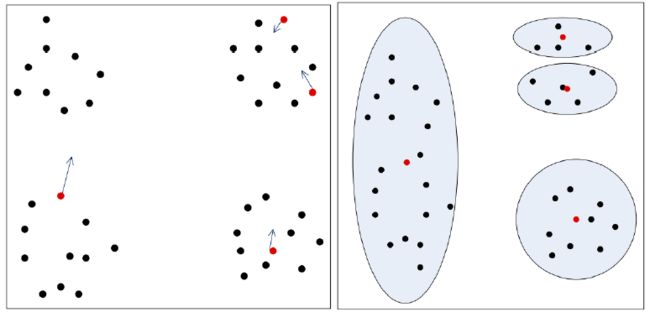
上边这幅图就比较形象的说明了K-means的过程了。

当然了，这种做法有道理么，我们怎么去解释呢？

我们不妨使用平方误差来作为目标函数：

既然目标函数是凸的，我们不妨对μ求偏导并令其等于零：

K-Mediods

我们现在来对K-means将簇中所有的点的均值作为新的质心，若簇中有有异常点，将导致均值偏离严重，我们用一组数据来说明一下：

数组1,2,3,4,100的均值为22，显然这个22离大多数1，2，3，4比较远，所以我们不妨将均值改为中值，这样的话聚类中心就是3，还是比较有道理的，这就是改进版的K-中值(K-Mediods)聚类。

K均值的另一种做法

我们首先随机选一个聚类中心，然后计算每个样本到我这个聚类中心A的距离，然后排序，下次根据距离的大小随机选一个样本做聚类中心，如果离A越近那么被选中的概率越小，这样选出的第二个聚类中心B也是比较有道理的。接着计算每个样本到聚类中心A和B的距离，保留距离小的作为新的距离排序，并标记为离得近的类别，接着在按照距离大小选第三个聚类中心，依然按照距离越大概率越大的方式去选。。。。直到找到了K个聚类中心为止。

K-means算法对初值是敏感的，以图说明：

如果这样的话，我们可以对聚类中心做一个处理：如果我们发现一个聚类中心的均方误差比其他的聚类中心大很多，并且有两个聚类中心均方误差很小离的又很近，那么我们就有理由认为可能聚类错了，这样的话就可以将大的聚类分成两个聚类中心聚类，小的聚类中心合并到一起。

总结：

优点：快速、简单，对处理大数据集，该算法保持可伸缩性和高效率。当簇近似高斯分布时，它的效果比较好。

缺点：必须是先给出k，而且对初值比较敏感，对于不同的初始值，可能会导致不同的结果。不适合发现非凸型的。对噪声和孤立点数据敏感

K-means算法可作为其他算法的基础算法。