简化版SMO算法Scala实现

主要从Python机器学习实战里面转换过来, 风格比较命令式, 大量的var变量

先导入需要的包

import scala.collection.mutable.ArrayBuffer
import scala.math.signum

建立一个支持向量的类

case class SVM(alpha: Array[Double], //支持向量对应的乘子
               y: Array[Double], //支持向量对应的标签
               sv: Array[Array[Double]], //支持向量
               b: Double,
               kel: (Array[Double], Array[Double]) => Double) {

  def predict(x: Array[Double]) = { //预测一个点, 书上的公式
    var sum = b
    alpha.indices.foreach {
      i => sum += alpha(i) * y(i) * kel(x, sv(i))
    }
    signum(sum)
  }
}

建立一个专门放核函数的对象

object Kennels {
  def innerProduct(x: Array[Double], y: Array[Double]): Double = {
    var sum = 0.0
    x.indices.foreach(i => sum += x(i) * y(i))
    sum
  }
}

主程序

object SVMGen extends App {
  //随机选择第二个变量
  def selectJ(i: Int, m: Int): Int = { 
    var j = i
    while (j == i) {
      j = util.Random.nextInt(m)
    }
    j
  }
  //裁剪alpha2 以满足不等式约束
  def clipAlpha(aj: Double, H: Double, L: Double): Double = if (aj > H) H else if (aj < L) L else aj



  //读取文件
  def fileLoader(path: String): (Array[Array[Double]], Array[Double]) = { 
    import io.Source
    val file = Source.fromFile(path)
    val simples = new ArrayBuffer[Array[Double]]
    val labels = new ArrayBuffer[Double]
    for (line <- file.getLines()) {
      val lineSplit = line.split("\\s")
      simples += lineSplit.dropRight(1).map(_.toDouble)
      labels += lineSplit.takeRight(1)(0).toDouble
    }
    (simples.toArray, labels.toArray)
  }

  def simpleSMO(dataMat: Array[Array[Double]], y: Array[Double], C: Double, kel: (Array[Double], Array[Double]) => Double, toler: Double, maxIter: Int): SVM = {
    val m = dataMat.length
    var alphaPairChanged, iter = 0
    var fXi, fXj, eta, Ei, Ej, alphaIold, alphaJold, L, H, b, b1, b2 = 0.0
    val alpha = new Array[Double](m)

    //定义一个输出g(x_i), 见李航书上p127
    def g(n: Int) = {
      var sum = b
      (0 until m).foreach(k => sum += alpha(k) * y(k) * kel(dataMat(n), dataMat(k)))
      sum
    }

    while (iter < maxIter) {
      alphaPairChanged = 0
      for (i <- 0 until m) {
        fXi = g(i)
        Ei = fXi - y(i) //计算Ei
        if ((Ei * y(i) < -toler && alpha(i) < C) || (Ei * y(i) > toler && alpha(i) > 0)) {
          val j = selectJ(i, m)
          fXj = g(j)
          Ej = fXj - y(j)
          alphaIold = alpha(i)
          alphaJold = alpha(j)
          // 计算L, 和H ,参见相关公式, 主要分i=j和i!=j两种情况
          if (y(i) != y(j)) {
            L = 0.0.max(alphaJold - alphaIold)
            H = C.min(C + alphaJold - alphaIold)
          }
          else {
            L = 0.0.max(alphaJold + alphaIold - C)
            H = C.min(alphaJold + alphaIold)
          }
          if (L == H) println("L == H, 下一轮")
          else {
            // eta =  K_11 + K_22 - 2*K_12, 注意这里和python版的不一样, 有一个负号的区别, 这是采用李航书上的公式
            eta = kel(dataMat(i), dataMat(i)) + kel(dataMat(j), dataMat(j)) - 2 * kel(dataMat(i), dataMat(j))
            if (eta < 0.00001) println("eta 太小或为负, 下一轮")
            else {
              alpha(j) = alphaJold + y(j) * (Ei - Ej) / eta
              alpha(j) = clipAlpha(alpha(j), H, L)
              if (math.abs(alpha(j) - alphaJold) < 0.00001) println("j not moving enough") // alphaJ 修改量太小就跳过
              else {
                alpha(i) = alphaIold + y(i) * y(j) * (alphaJold - alpha(j)) //更新alphaI
                // 更新b
                b1 = b - Ei - y(i) * kel(dataMat(i), dataMat(i)) * (alpha(i) - alphaIold)
                    -y(j) * kel(dataMat(j), dataMat(i)) * (alpha(j) - alphaJold)
                b2 = b - Ej - y(i) * kel(dataMat(i), dataMat(j)) * (alpha(i) - alphaIold)
                    -y(j) * kel(dataMat(j), dataMat(j)) * (alpha(j) - alphaJold)
                if (alpha(i) > 0 && alpha(i) < C) b = b1
                else if (alpha(j) > 0 && alpha(j) < C) b = b2
                else b = (b1 + b2) / 2.0
                alphaPairChanged += 1
                println("iter %d, alpha changed %d".format(iter, alphaPairChanged))
              }
            }
          }
        }
      }
      if (alphaPairChanged == 0) iter += 1 else iter = 0
      println("iteration number: %d".format(iter))
    }
    val svIndex = alpha.indices.filter(i => alpha(i) > 0).toArray // 挑选支持向量的编号
    val supportVectors = svIndex.map(i => dataMat(i)) //挑选支持向量
    val svY = svIndex.map(i => y(i)) //挑选标签
    new SVM(svIndex.map(i => alpha(i)), svY, supportVectors, b, kel) //创建一个支持向量机
  }


  val kel =  Kennels.innerProduct _ //导入核函数
  val (dataMat, y) = SVMGen.fileLoader("""/home/user/SMO/testSet.txt""") //读文件, 文件是python机器学习实战里面带的那个
  val svm1 = simpleSMO(dataMat, y, 0.7, kel, 0.0005, 40) //训练

  import breeze.plot._ //导入breeze-viz作图
  //预测一下训练集
  val posiSimples = dataMat.filter(svm1.predict(_)>0)
  val negaSimples = dataMat.filter(svm1.predict(_)<0)
  //作图
  val colorPalette = new GradientPaintScale(0.0, 1.0, PaintScale.Rainbow)
  val f2 = Figure()
  f2.subplot(0) += scatter( posiSimples.map(_(0)),posiSimples.map(_(1)), _ =>0.3, _=>colorPalette(0.28))
  f2.subplot(0) += scatter( negaSimples.map(_(0)),negaSimples.map(_(1)), _ =>0.3, _=>colorPalette(0.92))
  f2.subplot(0) += scatter(svm1.sv.map(_(0)),svm1.sv.map(_(1)), _=> 0.8)
  f2.saveas("svm.pdf")
}

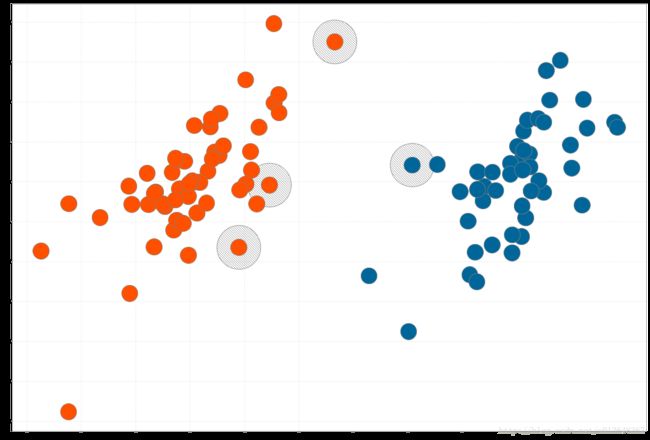
可见程序成功地找到了支持向量并且正确分类, 而且速度比Python快到不知道哪里去了