cs231n_assignment1_配置作业环境+kNN
作业1:http://cs231n.github.io/assignments2017/assignment1/
我是在win7电脑上做的。
准备工作:
下载anaconda:https://www.anaconda.com/download/
打开前修改jupyter notebook启动目录:https://www.zhihu.com/question/31600197/answer/90214029
jupyter notebook --generate-config
修改完成后,打开anaconda prompt
打开:jupyter notebook
如果有小伙伴还有困惑,可以参考我后来写的图文详细版,包你成功:Windows本地快速搭建cs231n作业环境
开始做作业
下载CIFAR-10数据库:http://www.cs.toronto.edu/~kriz/cifar.html,下载CIFAR-10 python version
解压到cs231n/datasets目录下,对每一个cell,shift+enter运行。
首先是加载数据:
由运行结果可以看出:
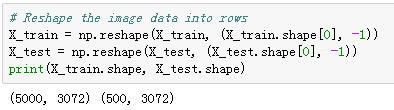
训练集50000张图片,每张图片是32*32*3的;测试集10000张图片,图片格式同上。
可视化数据集,每一个类随机选取7张图片:
numpy.flatnonzero(a):返回非0元素的索引,a可以是一个表达式
>>> x = np.arange(-2, 3)
>>> x
array([-2, -1, 0, 1, 2])
>>> np.flatnonzero(x)
array([0, 1, 3, 4])
可以使用它来提取非0元素:
>>> x.ravel()[np.flatnonzero(x)]
array([-2, -1, 1, 2])
numpy.random.choice(a, size=None, replace=True, p=None):对一维数组a产生一个随机采样。size指的是输出形状,replace表示放回还是不放回。
均匀分布:
>>> np.random.choice(5, 3)
array([0, 3, 4])
>>> #This is equivalent tonp.random.randint(0,5,3)
自定义取样概率:
>>> np.random.choice(5, 3, p=[0.1, 0, 0.3, 0.6, 0])
array([3, 3, 0])
>>> aa_milne_arr = ['pooh','rabbit', 'piglet', 'Christopher', 'dog', 'cat']
>>>np.random.choice(aa_milne_arr, 5, replace=False, p=[0.2, 0.1, 0.1, 0.3, 0.1,0.2])
array(['dog', 'piglet', 'pooh','cat', 'rabbit'], dtype='
为了后面减少计算量,随机采样数据集,训练集采样5000张,测试集采样500张:
将32*32*3的图片reshape成一行:
numpy.reshape(a, newshape, order='C')
np.reshape(a, (a.shape[1], a.shape[0])):转置等同于np.transpose(a)
当数据的形状不确定时,如果想转换为1行,列数不确定的话,newshape可以传入(1, -1);
如果想转换为1列,行数不确定的话,newshape可以传入(-1, 1);
同理如果是2列或者2行的话,就是(-1, 2)或者(2,-1)。 -1代表不确定
导入k近邻分类器模块:
利用两层循环计算L2距离:
-->
xrange() 函数用法与 range 完全相同,所不同的是生成的不是一个数组,而是一个生成器。Python3取消了xrange,只保留range。
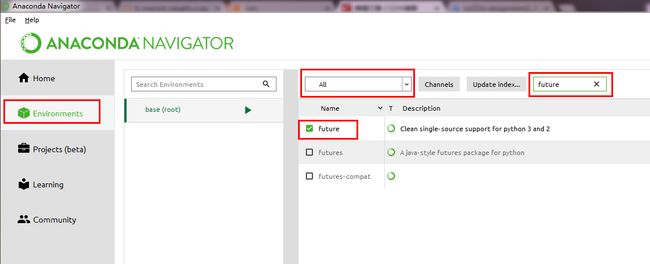
NoModuleError:No module named 'past',需要安装future包,在anaconda的environment里安装
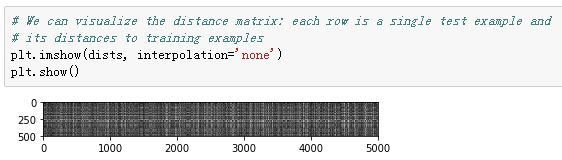
可视化距离矩阵:
knn不需要训练,直接进行预测,k=1:
-->
numpy.argsort(a, axis=-1, kind='quicksort', order=None)
排序,得到前k个近邻的标签,然后得到投票结果
numpy.bincount(x, weights=None, minlength=0)
对一维数组x统计各值出现的次数,x里必须是非负整数
numpy.argmax(a, axis=None, out=None)返回最大值
ValueError: object toodeep for desired array,关闭重启
再令k=5预测:
精度比k=1时稍高。
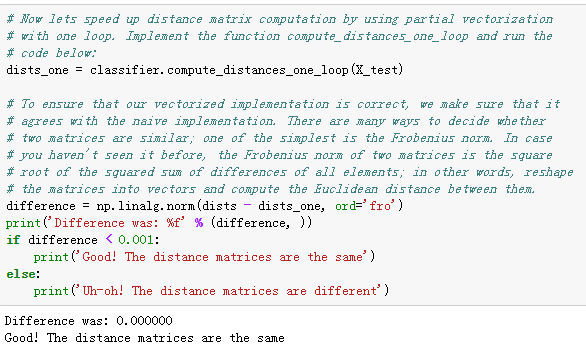
在一个loop中完成L2距离计算,并用F范数与两个loop时的结果比较验证正确性:
-->
利用numpy数组运算的特性(broadcast),自动进行维数扩展
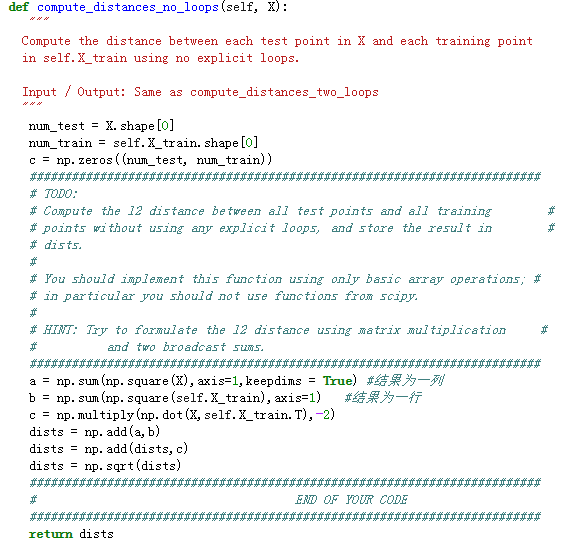
不使用loop计算L2距离:
-->
就是将距离函数拆开,完成各个单项后再合并
(x - y)^2 = x^2 - 2*x*y + y^2
a.dot(b) 与 np.dot(a,b)效果相同
numpy.sum():
keepdims :bool, optional
If this is set to True, the axes which are reduced are left in theresult as dimensions with size one. With this option, the result will broadcastcorrectly against the input array.
例如:
>>> b
array([[1, 2],
[3, 4],
[5, 6]])
>>> np.sum(b,axis=1,keepdims = True)
array([[ 3],
[ 7],
[11]])
>>> np.sum(b,axis=1)
array([ 3, 7, 11])
比较三种方法的优劣,高下立现:
交叉验证:
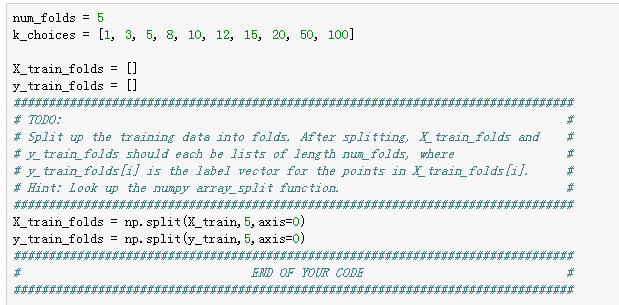
将训练集分成5等分,同时观察不同的k下的分类精度:
numpy.split(ary, indices_or_sections, axis=0)
Split an array into multiple sub-arrays.
>>> x = np.arange(9.0)
>>> np.split(x,3)
[array([ 0., 1., 2.]), array([ 3., 4., 5.]), array([ 6., 7., 8.])]
>>> x = np.arange(8.0)
>>> np.split(x,[3, 5, 6, 10])
[array([ 0., 1., 2.]),
array([ 3., 4.]),
array([ 5.]),
array([ 6., 7.]),
array([], dtype=float64)]
执行5次kNN算法,将其中一份数据作为验证集,其他作为测试集,取测试集的精度:
取平均精度,画出k-精度图:
可以看出,kNN的分类精度高也就30%,不实用。
最佳k咱们取10:
精度28.2%.