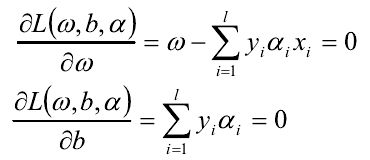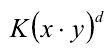svm支持向量机
支持向量机(support vector machine)是机器学习领域及其重要的一个算法,相比传统的神经网络,一方面,SVM的目标函数是一个凸函数,可以保证得到问题的全局最优解,避免了神经网络优化频繁陷入局部最优的困扰;另一方面,SVM的背后有一套结构化风险最小化的理论,给定了训练样本和训练参数,是可以从理论上计算出模型在真实数据上误差的bounds,有严密的数学理论作为支撑,而不像神经网络那样的黑箱模型。因此,在上个世纪末到这个世纪初,SVM横扫了各种分类的应用场景,成为了当时最炙手可热的机器学习算法。不过随着机器学习规模的爆炸式增长,svm不适合处理大数据的缺点凸显出来,随着深度学习的出现,曾经被svm踩在脚底下的神经网络又火了,火得一塌糊涂,人们蜂拥转向深度学习。但svm并不是没有用武之地了,在适合的场景,svm仍然是极好的分类问题解决方案。
虽然SVM已经有很多介绍的文章了,还是想自己写一个,加深下理解。
基本思想
支持向量机是从线性可分情况下的最优分类面发展而来的,其本质就是在于寻找一个把Rd空间的点分成两部分的规则。基本思想由下图中简单的线性可分的问题来说明,就是寻找一个最优分类超平面,使两类样本离超平面的距离最大化。图中,实心点和空心点代表两类样本,H 为最优分类超平面,1H 、2H 分别代表各类中离H 最近的样本且平行于H 的面,它们之间的距离称为分类间隔(Margin)。所谓最优化分类面或最大间隔超平面就是要求不但能将两类正确分开(训练错误率为0),而且使分类间隔最大。
线性可分情况
假定大小为L的训练样本集
(Xi,Yi ),Xi∈Rd, Yi∈{+1,-1 } ,i∈{ 1,2...,l}
由两个类别组成,如果Xi∈Rd属于第一类,则标记为正( Yi=1 ),否则,标记为负( Yi=-1 )。支持向量机的目的在于寻找分类超平面 H :
ωT+b=0T
使得样本集满足 :
Yi( ωT+b)-1>=0,i∈{ 1,2,...,l }
则此超平面可以将两类点分开。即使得两类中距离超平面最近点之间的距离最大。其中,ω是权重向量,b为偏置。两侧距离最优平面距离最短的向量称为支持向量。
点x到超平面H 的距离为:
根据最优分类超平面的定义,分类间隔可以表示为:
这里解释一下。想象一下要在线性可分的两堆数据(+,-)中间画一条线将它们分开,并使两类中距离分割线最近的点与分割线的距离最大,最终满足条件时肯定是两类中距离分割线最近的点与分割线的距离相等, 如果不是这样意味着一个近一个远,最大距离就是近的那个,而此时肯定还可以优化。
使间隔最大等价于使|| ω ||最小。则求最优分类超平面问题就转化为求在满足条件 且使 ||ω|| 最小的数学规划问题即:
s.t.表示subject to,约束条件。
约束条件的实际含义就是无论数据分为哪一类,该点距离分割线的距离都不小于1。
根据 Lagrange 定理求解上述问题的最优解:
其中:αi 为Lagrange乘子,对ω,b分别求偏导:
代入,(1)式的优化问题转化为其对偶问题
max:
s.t. ∑αi*yi=0,
αi>=0,
i=0,1,...,l
其中αi正是样本点xi的Lagrange乘子。
松弛变量
以上是基于数据完全线性可分的假设,所做的是硬间隔。但有时数据中含有噪点,为了得到最优的分割线,我们允许有个别点分类错误,为此引入了松弛变量C。
目标函数变为求下式的极小值:
s.t. yi(WTx+b)>=1-ξi,i=1,2,...,l。l为样本数量
ξi>=0
约束条件的意义是此时可以允许数据点距离分割线的距离小于1,可以有个别点错分,是软间隔。但此时要为代价函数添加一项C∑ξi,C代表惩罚系数,当C为无穷大时,也就是不允许有点被错分,就又变成了硬间隔。后面你会看到,分类正确的点对应的ξi=0,只有与分割线距离小于1的点对应的ξi>0。
此时我们的优化函数没有改变,约束条件有所改变
max:
s.t. ∑αi*yi=0,
0<=αi<=C,
i=0,1,...,l
仅当 αi=C 时出现非零松弛变量。
其中偏置b没有出现在对偶问题中,利用原始约束得:
最后得到的分类函数就为:
X为待测试样本,ai,yi,Xi和b*都是已知量,带入X的值后看整体计算后的正负,用sign取符号后输出+1或-1,即完成分类。
其中ω* 和b* 分别为最优超平面所对应的权重向量和偏置,最终通过求解α 而求得。
所以α的求取是SVM算法的关键。下面介绍一种求取α的算法——SMO算法。
SMO算法
SMO是序列最小优化(Sequential Minimal Optimization),是一种二次规划优化算法。
SMO算法把问题分解到可能达到的最小规模:每次优化只处理两个样本的优化问题,就是优化它们对应的Lagrange乘子,在其他参数固定的前提下,找到这两个参数的最优值,并更新相应的α向量。为什么要同时优化两个α呢?因为有约束条件:∑αi*yi=0, i=0,1,...,l。
当然,这样一次“最小优化”不可能保证其结果就是所优化的Lagrange乘子的最终结果,但会使目标函数向极值迈进一步。我们再对其它Lagrange乘子做最小优化,直到所有乘子都符合KKT条件时,目标函数达到最大,算法结束。
关于KKT条件,请看博客http://blog.csdn.net/xianlingmao/article/details/7919597。
***************************************************************************************************************************
*分割线之间的内容来自http://blog.csdn.net/techq/article/details/6171688
SVM是一个凸二次规划问题,凸二次规划问题有最优解,于是问题转换成下列形式(KKT条件):
![]() …………(1)
…………(1)
这里的ai是拉格朗日乘子(问题通过拉格朗日乘法数来求解)
对于(a)的情况,表明ai是正常分类,在边界内部(我们知道正确分类的点yi*f(xi)>=0)
对于(b)的情况,表明了ai是支持向量,在边界上
对于(c)的情况,表明了ai是在两条边界之间
而最优解需要满足KKT条件,即满足(a)(b)(c)条件都满足
以下几种情况出现将会出现不满足:
yiui<=1但是ai
yiui=1但是ai=0或者ai=C则表明不满足的,而原本应该是0
![]()
因此,我们通过另一个方法,即同时更新ai和aj,满足以下等式
![]()
就能保证和为0的约束。
利用yiai+yjaj=常数,消去ai,可得到一个关于单变量aj的一个凸二次规划问题,不考虑其约束0<=aj<=C,可以得其解为:
![]() ………………………………………(2)
………………………………………(2)
这里![]() ………………(3)
………………(3)
表示旧值,然后考虑约束0<=aj<=C可得到a的解析解为:
![]() …………(4)
…………(4)
![]()
对于![]()
那么如何求得ai和aj呢?
对于ai,即第一个乘子,可以通过刚刚说的那几种不满足KKT的条件来找,第二个乘子aj可以找满足条件
![]() …………………………………………………………………………(5)
…………………………………………………………………………(5)
b的更新:
![]()
在满足条件:
![]() 下更新b。……………(6)
下更新b。……………(6)
最后更新所有ai,y和b,这样模型就出来了,然后通过函数:
![]() ……………………………………………………(7)
……………………………………………………(7)
输入是x,是一个数组,组中每一个值表示一个特征。
输出是A类还是B类。(正类还是负类)
***************************************************************************************************************************
SMO函数粗略的伪码如下:
while(i
changed=false
选择第一个alpha的值,任何违反KKT条件的乘子(或样本)都是合法的第一个拉格朗日乘子
通过最大化步长方式得到第二个alpha
同时优化两个乘子
如果乘子与原来相比有变化,changed=true
直到找不到需要改变的乘子,跳出循环
对于大多数样本来讲,对应的αi=0,对应αi≠0的样本称为支持向量(Support Vector,SV)。
核函数
SVM 可以通过核函数 ( yxK ,)映射实现非线性数据分类,其基本原理如下图所示
核函数对输入空间进行非线性映射
通过核函数可以将输入空间中线性不可分的特征向量非线性映射为输出特征空间中,变得线性可分。通常使用的有以下3种核函数用于非线性变换:
a. 多项式核函数
参数 d 为多项式次数;
b. 高斯径向基函数
参数σ^2 为高斯函数的方差;
c. S 函数
tanh( α ( x⋅y ) + β )
参数α 为变换尺度, β 为偏置。
这样问题就可以表述为:输入向量X通过映射ψ:Rn一H影射到高维空问H中,核函数为K(Xi,Xj)=ψ(Xi)·ψ(Xj),这里是向量点乘,则优化问题转化为
用之前的方法,解出的最优化函数为:
所以不需要知道H和ψ,只需要选择合适的核函数K(·)和C就可以确定SVM。
svm如何判断线性可分
分割线之间的内容来自SVM:如何判断线性可分
/**************************************************************************/
支持向量机(SVM),介绍都说了假设数据要是线性可分。
如果数据不是线性可分的,我们就必须要采用一些特殊的方法,比如SVM的核技巧把数据转换到更高的维度上,在那个高维空间数据更可能是线性可分的(Cover定理)。
现在的问题是,如何判断数据是线性可分的?
最简单的情况是数据向量是一维二维或者三维的,我们可以把图像画出来,直观上就能看出来。
比如Håvard Geithus网友的图,非常简单就看出两个类的情形下X和O是不是线性可分。
但是数据向量维度一旦变得很高,我们怎么办?
答案是:检查凸包(convex hull)是否相交。
什么是凸包呢?
简单说凸包就是一个凸的闭合曲线(曲面),而且它刚好包住了所有的数据。
举个例子,下图的蓝色线就是一个恰好包住所有数据的闭合凸曲线。
知道了什么是凸包,我们就能检查我们的数据是不是线性可分了。
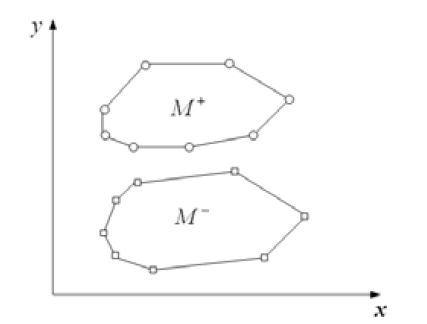
以二维的情况为例,如果我们的数据训练集有两类:M+和M-,
当我们画出两个类的凸包,如果两者不重叠,那么两者线性可分,反之则不是线性可分。
下图就是个线性可分的情况。
虽然现在我们比直接看数据判断是不是线性可分进了一步,但是好像还是靠画出图来人眼判断,这对高维度数据依然无效。
是这样么?当然不是。
因为判断两个凸包是不是有重叠可以通过判断凸包M+的边和凸包M-的边是否相交来实现,这就无需把凸包画出来了。
如何高效的找到一组数据的凸包?
如何高效的判断两个凸包是否重合?
网友Darren Engwirda 给出了很好的建议:
There are efficient algorithms that can be used both to find the convex hull (theqhull algorithm is based on anO(nlog(n)) quickhull approach I think), and to perform line-line intersection tests for a set of segments (sweepline atO(nlog(n))), so overall it seems that an efficient O(nlog(n)) algorithm should be possible.
This type of approach should also generalise to general k-way separation tests (where you havekgroups of objects) by forming the convex hull and performing the intersection tests for each group.
It should also work in higher dimensions, although the intersection tests would start to become more challenging...
简单说,他的建议就是用quickhull算法来找到数据的凸包,sweepline算法判断凸包边缘是否有相交,两个步骤的复杂度都是O(nlogn)。
其中quickhull已经在软件包qhull(http://www.qhull.org/)实现了。
--------------------- 本文来自 macb007 的CSDN 博客 ,全文地址请点击:https://blog.csdn.net/macb007/article/details/78887282?utm_source=copy
SVM处理多类问题
SVM最初是用来解决两类分类问题的,不能直接用于解决多分类问题。目前解决多类问题的途径主要有两个:一个就是 Weston等人提出多类算法为代表。这个算法在经典 SVM 理论的基础上,重新构造多值分类模型,通过SVM 方法对新模型的目标函数进行优化,实现多值分类,使支持向量机本身成为解决多类分类问题的多类分类器。
总结
SVM在解决小样本、非线性及高维模式识别问题中表现出许多特有的优势,并能够推广应用到函数拟合等其他机器学习问题中。
'''
Created on Nov 4, 2010
Chapter 5 source file for Machine Learing in Action
@author: Peter
'''
from numpy import *
from time import sleep
def loadDataSet(fileName):
dataMat = []; labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]), float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat,labelMat
def selectJrand(i,m):
j=i #we want to select any J not equal to i
while (j==i):
j = int(random.uniform(0,m))
return j
def clipAlpha(aj,H,L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
dataMatrix = mat(dataMatIn); labelMat = mat(classLabels).transpose()
b = 0; m,n = shape(dataMatrix)
alphas = mat(zeros((m,1)))
iter = 0
while (iter < maxIter):
alphaPairsChanged = 0
for i in range(m):
fXi = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
Ei = fXi - float(labelMat[i])#if checks if an example violates KKT conditions
if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
j = selectJrand(i,m)
fXj = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b
Ej = fXj - float(labelMat[j])
alphaIold = alphas[i].copy(); alphaJold = alphas[j].copy();
if (labelMat[i] != labelMat[j]):
L = max(0, alphas[j] - alphas[i])
H = min(C, C + alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C, alphas[j] + alphas[i])
if L==H: print "L==H"; continue
eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
if eta >= 0: print "eta>=0"; continue
alphas[j] -= labelMat[j]*(Ei - Ej)/eta
alphas[j] = clipAlpha(alphas[j],H,L)
if (abs(alphas[j] - alphaJold) < 0.00001): print "j not moving enough"; continue
alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])#update i by the same amount as j
#the update is in the oppostie direction
b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
if (0 < alphas[i]) and (C > alphas[i]): b = b1
elif (0 < alphas[j]) and (C > alphas[j]): b = b2
else: b = (b1 + b2)/2.0
alphaPairsChanged += 1
print "iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged)
if (alphaPairsChanged == 0): iter += 1
else: iter = 0
print "iteration number: %d" % iter
return b,alphas
def kernelTrans(X, A, kTup): #calc the kernel or transform data to a higher dimensional space
m,n = shape(X)
K = mat(zeros((m,1)))
if kTup[0]=='lin': K = X * A.T #linear kernel
elif kTup[0]=='rbf':
for j in range(m):
deltaRow = X[j,:] - A
K[j] = deltaRow*deltaRow.T
K = exp(K/(-1*kTup[1]**2)) #divide in NumPy is element-wise not matrix like Matlab
else: raise NameError('Houston We Have a Problem -- \
That Kernel is not recognized')
return K
class optStruct:
def __init__(self,dataMatIn, classLabels, C, toler, kTup): # Initialize the structure with the parameters
self.X = dataMatIn
self.labelMat = classLabels
self.C = C
self.tol = toler
self.m = shape(dataMatIn)[0]
self.alphas = mat(zeros((self.m,1)))
self.b = 0
self.eCache = mat(zeros((self.m,2))) #first column is valid flag
self.K = mat(zeros((self.m,self.m)))
for i in range(self.m):
self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)
def calcEk(oS, k):
fXk = float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b)
Ek = fXk - float(oS.labelMat[k])
return Ek
def selectJ(i, oS, Ei): #this is the second choice -heurstic, and calcs Ej
maxK = -1; maxDeltaE = 0; Ej = 0
oS.eCache[i] = [1,Ei] #set valid #choose the alpha that gives the maximum delta E
validEcacheList = nonzero(oS.eCache[:,0].A)[0]
if (len(validEcacheList)) > 1:
for k in validEcacheList: #loop through valid Ecache values and find the one that maximizes delta E
if k == i: continue #don't calc for i, waste of time
Ek = calcEk(oS, k)
deltaE = abs(Ei - Ek)
if (deltaE > maxDeltaE):
maxK = k; maxDeltaE = deltaE; Ej = Ek
return maxK, Ej
else: #in this case (first time around) we don't have any valid eCache values
j = selectJrand(i, oS.m)
Ej = calcEk(oS, j)
return j, Ej
def updateEk(oS, k):#after any alpha has changed update the new value in the cache
Ek = calcEk(oS, k)
oS.eCache[k] = [1,Ek]
def innerL(i, oS):
Ei = calcEk(oS, i)
if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
j,Ej = selectJ(i, oS, Ei) #this has been changed from selectJrand
alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();
if (oS.labelMat[i] != oS.labelMat[j]):
L = max(0, oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else:
L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
if L==H: print "L==H"; return 0
eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] #changed for kernel
if eta >= 0: print "eta>=0"; return 0
oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta
oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
updateEk(oS, j) #added this for the Ecache
if (abs(oS.alphas[j] - alphaJold) < 0.00001): print "j not moving enough"; return 0
oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as j
updateEk(oS, i) #added this for the Ecache #the update is in the oppostie direction
b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]
b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]
if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1
elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2
else: oS.b = (b1 + b2)/2.0
return 1
else: return 0
def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup=('lin', 0)): #full Platt SMO
oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler, kTup)
iter = 0
entireSet = True; alphaPairsChanged = 0
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
alphaPairsChanged = 0
if entireSet: #go over all
for i in range(oS.m):
alphaPairsChanged += innerL(i,oS)
print "fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged)
iter += 1
else:#go over non-bound (railed) alphas
nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
for i in nonBoundIs:
alphaPairsChanged += innerL(i,oS)
print "non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged)
iter += 1
if entireSet: entireSet = False #toggle entire set loop
elif (alphaPairsChanged == 0): entireSet = True
print "iteration number: %d" % iter
return oS.b,oS.alphas
def calcWs(alphas,dataArr,classLabels):
X = mat(dataArr); labelMat = mat(classLabels).transpose()
m,n = shape(X)
w = zeros((n,1))
for i in range(m):
w += multiply(alphas[i]*labelMat[i],X[i,:].T)
return w
def testRbf(k1=1.3):
dataArr,labelArr = loadDataSet('testSetRBF.txt')
b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', k1)) #C=200 important
datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
svInd=nonzero(alphas.A>0)[0]
sVs=datMat[svInd] #get matrix of only support vectors
labelSV = labelMat[svInd];
print "there are %d Support Vectors" % shape(sVs)[0]
m,n = shape(datMat)
errorCount = 0
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
if sign(predict)!=sign(labelArr[i]): errorCount += 1
print "the training error rate is: %f" % (float(errorCount)/m)
dataArr,labelArr = loadDataSet('testSetRBF2.txt')
errorCount = 0
datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
m,n = shape(datMat)
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
if sign(predict)!=sign(labelArr[i]): errorCount += 1
print "the test error rate is: %f" % (float(errorCount)/m)
def img2vector(filename):
returnVect = zeros((1,1024))
fr = open(filename)
for i in range(32):
lineStr = fr.readline()
for j in range(32):
returnVect[0,32*i+j] = int(lineStr[j])
return returnVect
def loadImages(dirName):
from os import listdir
hwLabels = []
trainingFileList = listdir(dirName) #load the training set
m = len(trainingFileList)
trainingMat = zeros((m,1024))
for i in range(m):
fileNameStr = trainingFileList[i]
fileStr = fileNameStr.split('.')[0] #take off .txt
classNumStr = int(fileStr.split('_')[0])
if classNumStr == 9: hwLabels.append(-1)
else: hwLabels.append(1)
trainingMat[i,:] = img2vector('%s/%s' % (dirName, fileNameStr))
return trainingMat, hwLabels
def testDigits(kTup=('rbf', 10)):
dataArr,labelArr = loadImages('trainingDigits')
b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, kTup)
datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
svInd=nonzero(alphas.A>0)[0]
sVs=datMat[svInd]
labelSV = labelMat[svInd];
print "there are %d Support Vectors" % shape(sVs)[0]
m,n = shape(datMat)
errorCount = 0
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],kTup)
predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
if sign(predict)!=sign(labelArr[i]): errorCount += 1
print "the training error rate is: %f" % (float(errorCount)/m)
dataArr,labelArr = loadImages('testDigits')
errorCount = 0
datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
m,n = shape(datMat)
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],kTup)
predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
if sign(predict)!=sign(labelArr[i]): errorCount += 1
print "the test error rate is: %f" % (float(errorCount)/m)
'''#######********************************
Non-Kernel VErsions below
'''#######********************************
class optStructK:
def __init__(self,dataMatIn, classLabels, C, toler): # Initialize the structure with the parameters
self.X = dataMatIn
self.labelMat = classLabels
self.C = C
self.tol = toler
self.m = shape(dataMatIn)[0]
self.alphas = mat(zeros((self.m,1)))
self.b = 0
self.eCache = mat(zeros((self.m,2))) #first column is valid flag
def calcEkK(oS, k):
fXk = float(multiply(oS.alphas,oS.labelMat).T*(oS.X*oS.X[k,:].T)) + oS.b
Ek = fXk - float(oS.labelMat[k])
return Ek
def selectJK(i, oS, Ei): #this is the second choice -heurstic, and calcs Ej
maxK = -1; maxDeltaE = 0; Ej = 0
oS.eCache[i] = [1,Ei] #set valid #choose the alpha that gives the maximum delta E
validEcacheList = nonzero(oS.eCache[:,0].A)[0]
if (len(validEcacheList)) > 1:
for k in validEcacheList: #loop through valid Ecache values and find the one that maximizes delta E
if k == i: continue #don't calc for i, waste of time
Ek = calcEk(oS, k)
deltaE = abs(Ei - Ek)
if (deltaE > maxDeltaE):
maxK = k; maxDeltaE = deltaE; Ej = Ek
return maxK, Ej
else: #in this case (first time around) we don't have any valid eCache values
j = selectJrand(i, oS.m)
Ej = calcEk(oS, j)
return j, Ej
def updateEkK(oS, k):#after any alpha has changed update the new value in the cache
Ek = calcEk(oS, k)
oS.eCache[k] = [1,Ek]
def innerLK(i, oS):
Ei = calcEk(oS, i)
if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
j,Ej = selectJ(i, oS, Ei) #this has been changed from selectJrand
alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();
if (oS.labelMat[i] != oS.labelMat[j]):
L = max(0, oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else:
L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
if L==H: print "L==H"; return 0
eta = 2.0 * oS.X[i,:]*oS.X[j,:].T - oS.X[i,:]*oS.X[i,:].T - oS.X[j,:]*oS.X[j,:].T
if eta >= 0: print "eta>=0"; return 0
oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta
oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
updateEk(oS, j) #added this for the Ecache
if (abs(oS.alphas[j] - alphaJold) < 0.00001): print "j not moving enough"; return 0
oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as j
updateEk(oS, i) #added this for the Ecache #the update is in the oppostie direction
b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[i,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[i,:]*oS.X[j,:].T
b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[j,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[j,:]*oS.X[j,:].T
if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1
elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2
else: oS.b = (b1 + b2)/2.0
return 1
else: return 0
def smoPK(dataMatIn, classLabels, C, toler, maxIter): #full Platt SMO
oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler)
iter = 0
entireSet = True; alphaPairsChanged = 0
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
alphaPairsChanged = 0
if entireSet: #go over all
for i in range(oS.m):
alphaPairsChanged += innerL(i,oS)
print "fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged)
iter += 1
else:#go over non-bound (railed) alphas
nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
for i in nonBoundIs:
alphaPairsChanged += innerL(i,oS)
print "non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged)
iter += 1
if entireSet: entireSet = False #toggle entire set loop
elif (alphaPairsChanged == 0): entireSet = True
print "iteration number: %d" % iter
return oS.b,oS.alphas
OpenCV中CvSVM部分函数解读
SVM:从理论到OpenCV实践
OpenCV解析SVM
SVM与C++源码实现
SVM学习总结
支持向量机(一)
支持向量机(二)
支持向量机(三)