后·冯诺依曼时代,一场计算机革命悄然来临
后·冯诺依曼时代,一场计算机革命悄然来临
号称能够满足区块链扩展性要求的Blockchain3.0们,没有一百也有八十。这其中除开大部分的空气项目,真正有创新有作为的候选者,在笔者看来屈指可数。它们大都通过sharding或者Layer 2的方案在传统的冯诺依曼体系架构下修修补补,不能说这样的选择有错。其实可扩展性难题来自于区块链之外,而在这些Blockchain3.0项目中,有一个却意义非凡–它尝试从最根本的层次上解决可扩展性难题。
可扩展性之痛
可扩展性(scalability)是系统总体容量(吞吐率)能够随节点数增加而线性增加的能力。
这个看似简单的要求却需要顽强的努力和精湛的技艺才能针对性地在某个特定领域内的实现。
- 从程序设计的角度来说,必须针对性地设计来协调多台服务器。设计能够无限扩展的程序和只需要运行在单节点的程序在难度上不可同日而语。
- 从运维的角度来说,支撑大规模分布式系统的稳定运行异常的艰辛和繁琐。为了实现N个9的SLA,从部署、磁盘存储到网络,都需要针对性地设计运维方案和灾备预案。
扩展性难题不仅仅是区块链需要解决的问题,同时也是传统软件工程中挥之不去的阴霾。
跛行千里
扩展性难题由来已久,业界一直都在不断尝试,寻求一种普适的方法来破解扩展性难题。
DevOps 从PaaS到docker,再到容器编排系统,业界发展了不可胜举的工具、流程。在一定程度上确实降低了解决扩展性难题的门槛。 比如:在Google Cloud Platform上使用Kubernete部署和运维。特别是通过Autoscaler自动地添加或者裁剪Pod集群,笔者切身地感受到了K8S带来的便利。但DevOps并没有解决扩展性难题 – 由于各类资源对于程序并不是透明的,因此程序在设计之初就需要考虑运行环境并针对性地设计和优化,特别是对于数据共享、分布式存储设计仍久有诸多挑战。
Serverless
近两年来兴起的Serverless框架,典型代表是亚马逊的AWS Lambda
和谷歌的Google Cloud Functions。它们都致力于提供一个开发框架,在此框架内编写的代码能够在它们的云平台上获得无限扩展的能力。Serverless并不是说没有服务器。它指的是代码的编写完全不需要考虑运行环境。而支撑Serverless程序运行的基础设施(服务器、存储、网络)的复杂操作都交给了云平台。当系统容量不够时,云平台自动地扩展基础设施,而所有这一切对于程序是透明的。这样一种解决方略卓有成效,使用这些巨无霸公司提供的产品固然可以解决问题,
它们将最复杂的分布式任务调度、编排、基础设施灾备这些都隐藏起来,但使用它们的产品同样也意味着“技术绑架”,限制扩展性的因素变成了信用卡上的剩余额度。
一路行来,业界取得的成就有目共睹。但似乎缺乏从根本上彻底解决可扩展性难题的勇气?
可扩展性难题的根源在哪?
尽管编程语言越来越多, 但它们都走进了同一个死胡同 – “λ演算” 。– 包括C++、C#、Java、Scala、Haskell、Python、Erlang、Golang等等,基本上只要你能叫出名字的编程语言,都源于“λ演算” 。
λ演算(Lambda-Calculus)是最基本的编程语言。它最早是由Alonzo Church(图灵的博导)在20世纪30年代引入,之后的Church–Turing thesis证明了λ演算与图灵机是等价的。随后的50年代,以随机存储器为特征、通过纸带输入的冯诺依曼计算机的面世,λ演算有了用武之地。在输入指令的时候,为了避免重复劳动复用某个功能,将这个功能的指令打包成一条纸带。每当需要用到这个功能时就输入这条纸带,这条纸带就可以视为λ演算中的函数(function),它将一组指令打包后允许重复地调用。即使发展到今天,虽没有了纸带,但本质上并没有任何改变 – 基于“λ演算”的语言的特征就是对函数调用的聚集。
λ演算和冯诺依曼计算机相辅相成,奠定了当今信息时代的辉煌成就。但是单一计算节点总是存在容量瓶颈,为了提高系统的整体容量,必须让多台计算机组成一个整体协同工作。
而可扩展性难题的根源就在于目前主流的冯诺依曼体系架构,因为它是不可组合的; 计算机与计算机之间的边界对于λ演算并不是透明的。即,两台冯诺依曼计算机加在一起还是两台独立的计算机。这种隔阂对于程序来说是不可忽视的,也就导致了前文中提到的难题。
破解之道
既然根源在于缺乏可组合性(Compositionality),那么根本性的解决之道呼之欲出。
λ演算从上世纪创立后并没有停止发展,在它的基础上逐渐发展出了以Rho演算(Rho-Calculus)和ϕ演算(Phi-Calculus)为代表的高阶演算(Higher Order Calculus)。其中Rho演算最为接近实用,它已经被成功地应用到了微软BizTalk服务中。从Rho演算衍生出的Rholang编程语言以及RhoVM虚拟机已经发布了0.6版本。
RhoVM虚拟出基于Rho演算的计算机–RhoMachine,而Rholang就运行在RhoMachine中。RhoVM虽然运行于冯诺依曼计算机之上,却和冯诺依曼计算机有本质的区别–它虚拟出的RhoMachine是可组合的!
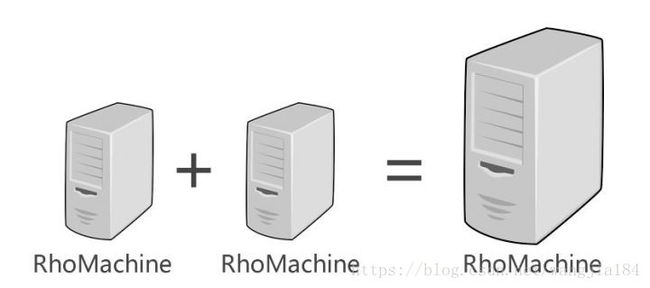
多台RhoMachine可以组成一台RhoMachine,这对于Rholang程序来说是完全透明的。从程序的视角来看,只有一台RhoMachine,这台RhoMachine可能由多台RhoMachine组成,但是程序并不关心,这样RhoMachine的总体容量不再受限于单个物理节点,同时程序在设计和运维上也不需要为特定场景针对性地制定方案。
想知道Rho演算为什么具有可组合性?最直观的方式是从Rholang切入理解它的工作方式。《初始Rholang》和《元组空间》这两篇文章从原理上解释了可组合性的缘由。
Rholang设计为一种通用的编程语言,而RChain区块链项目只是它实践的第一个项目–搭建一台可以无限扩展的超级计算机。因此可以说Rho演算的征途是星辰大海,它的愿景是一劳永逸地从根本上解决冯诺依曼体系带来的弊端。
后·冯诺依曼
后·冯诺依曼时代已经悄悄来临,这是一片荒芜之地,也是一片可以大展拳脚的“蓝海”。可扩展性难题只是冯诺依曼计算机被诟病的众多缺点之一。Rho演算带来的不仅仅是可组合性一个特性,它还有其它许多方面的优势,比如程序可以随时中断随后恢复、数据优先、代码与数据一体 等。
Rho演算做为后·冯诺依曼时代的基础理论,必将在这场革命中发挥重要作用!