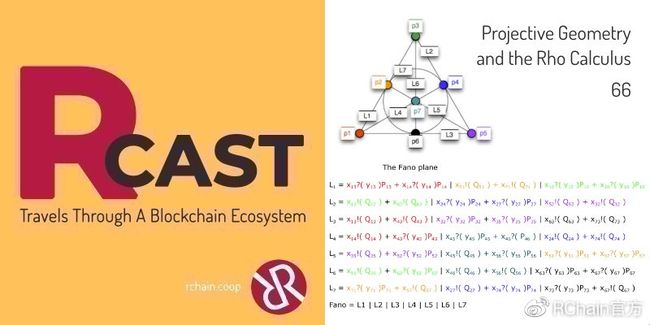
Greg Meredith与Isaac DeFrain和Christian Williams一起讨论了射影几何及其在Rho演算中的作用。
https://blog.rchain.coop/blog/2020/01/11/rcast-66-projective-geometr
讨论
指导原则之一:线是相互作用的点。形式上,这意味着线可以被解释为一系列过程,而点则是(一组)redex。所有可能的redex都已进行了颜色编码,以与图中各点的颜色匹配。例如,标记为p1的点以红色显示在L1,L3和L4上。因此,我们预计L1可能会随着L3的减少而减少,并且在各平行组成部分的两个红色部分中也会减少。同样,L1与L4会与红色并行和交互,L3和L4同样如此。
要从此骨架进行到仅在(一定数量)交互(从而能够提供稳定的几何形状)之后重现Fano平面的过程,要解决只有Pij和Qij。以下是一个简单的练习,但是你可能会发现这个小技巧会有所帮助。
x?(y)( *y | x!(y) ) | x!( x?(y)( *y | x!(y) ) | P ) ->* P | P | P | ….
构造Pij和Qij的解决方案更加有趣,因为随着线的相互作用,整个空间会演化为新的几何形状。
观察
转向构图几何
这种方法有关键特性——几何形状是可以被合成的。在最简单的情况下,仅通过并行组合就可以将几种几何形状合并为更大的几何形状。我们可以将它与……cobordisms的机制进行比较。
几何与逻辑的关系
实际上,框架比过程更接近于空间行为类型,这表明了一种与Curry-Howard的隐式对齐。
通过图形编码分解编码
作为最终观察,这种特定的编码方法并不限定于Fano平面,而是直接从与几何图形关联的图形中得出。问题在于,对图形的不同π-演算编码如何与在表示几何形状和几何形状演化方面进行比较。例如,Gardner等人在模型XML文档的上下文中探索了基于π演算的图形编码。他们对图形进行编码的策略提供了关于几何演化的不同见解。
整理稿
Greg: 我想回顾一下大约一周前在Casper分享系列中所提到的一些工作。我认为对于RCast而言是个很好的话题。这是技术性的,但却是有趣的技术性内容。让我们快速过一下幻灯片。促使我谈论这个话题的原因,是因为去年秋天, Nima Arkani-Hamed在哈佛物理学上所开设的一门课程。该讲座系列名为“时空和量子力学,总正性和动力”。在发出虚拟粒子的情况下,他采用的是计算粒子相互作用的散射幅度的方法;一切都是on shell的。他证明了正Grassmannian是直接与放大面体相连的,并为这些散射幅度提供了非常好的、清晰的计算。这是一个非常有趣的观点。
他得到了一种用于计算的图形重写形式,这与我考虑计算模型、尤其是Rho演算之类的想法非常相似。我意识到自己在大约十年前做过这项工作,我会向大家展示,你可以将更直接的几何编码输入到过程代数设置中。
我们曾经谈到过“结作为流程(Knots as Processes)”这个话题。这种拓扑信息实际上与几何信息不同。几何信息更加详细。类型学不能保留距离之类的东西。我不会去对类似欧几里得的几何图形进行编码,但是我要做的是射影几何图形。
特别是,我会将讨论范围限定在对有限的投影几何体(例如Fano平面)进行编码,这是最简单的示例。此处重点是,虽然LADL(逻辑作为分配法则)作为一种算法可以为各种各样的代数和演算生成类型系统,因此可以应用于像Clifford代数这样对几何信息进行编码的地方,但这是不同的。是否可以将几何信息直接编码到过程代数设置中?我在这里停一下,我说的大家都听得懂吗?
Isaac: 能听懂。这使人联想到Erlangen程序。对于诸如连接、相似点、不同点……之类的,你有什么想说的吗?
Greg: 我们来让听众们回忆一下Erlangen程序是什么吧。
Christian: 我对Erlangen程序的印象是从群论和射影几何学角度对几何学进行某种代数分类。
Greg: 对。很高兴你这么说了,因为它会再回到 LADL(逻辑作为分配法则)的话题。如果我可以针对各种几何或几何空间提出一个不错的过程代数编码,那么我就可以为正在使用的特定过程代数框架采用类型系统。这就成为了一种分类机制。它完全符合Erlangen程序的意图。
Christian: 所以,这就像是几何的类型分类吗?
Greg: 没错。
Christian: 合并几何的动机是什么?
Greg: 我可以告诉你当时我最直接的动机是什么。在考虑这一点期间,我一直与许多生物学家保持交流。我很清楚,Shapiro,Habib和Cardeli所做的工作对于在这些细胞信号网络和其他生物成员中捕获动态信息的某些动态方面很重要。归根结底,很多信息确实需要依赖几何信息,因为这些网络中的许多动态都依赖于几何信息——蛋白质折叠就是最好的例子。我并不是真的想要解决蛋白质折叠问题或其他真正的几何问题。我只是想亲自看看,我是否可以在这种情况下以合理的方式对几何信息进行编码?答案是肯定的。
这段对话还有另一方面。Bob Coecke在谈论他为量子力学开发的图形语言时提出了一个观点。他指出,使用量子力学的标准表示法,人们花费了60年的时间才发现了量子的隐形传态。然而,当你使用他和Aleks Kissinger所开发的图形表示时,你立即就能发现量子隐形传态。
不同的演示方法确实会让你大吃一惊。不是说他们脱离了你的想象范围,而是他们提出了各种问题。同样的,爱因斯坦和希尔伯特在考虑广义相对论时,他们所考虑的并不是组成性;他们并没有考虑对动力系统进行双仿真——即探讨在什么情况下,不同的演示可能会产生相同的动力系统;他们考虑的不是基于类型的分类。
但是事实证明,所有这些事情都是当场呈现的。对于爱因斯坦来说,希尔伯特的真正绊脚石不是静态几何,而是动态几何。爱因斯坦花了很长时间才获得了应力-能量张量和度量张量之间的递归关系,应力-能量张量分配的是物质和能量,而度量张量则会告诉你空间是如何翘曲的。
Isaac: 就是你所说的动态几何的意思吗,应力-能量张量和度量张量之间的相互作用?
Greg: 这种说法很物理。我的意思是,几何会随着时间而发展。欧几里得没有讨论欧几里得几何的演变,例如,演变为双曲线几何。Remonde没有讨论双曲几何向射影几何的演变。但是,一旦完成演示,我们就能直观地看到几何形状是如何不断进行演变的。它马上就会呈现出来。这就是为什么它很有趣的原因所在——演示使不同的问题立即变得显而易见起来。
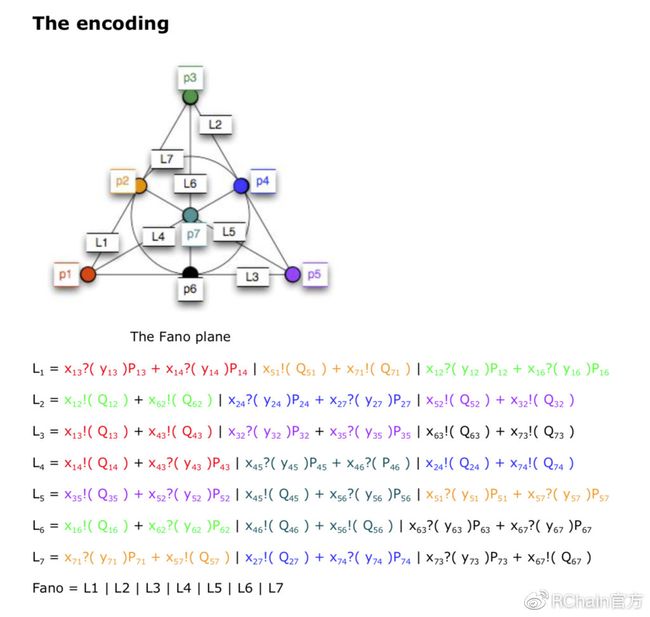
Fano平面是由一些点和线所定义的。七行中有七个点,每个点在三行中,每行包含三个点。如果尝试在欧几里得几何图形中绘制该图形,你必将失败,因为必须中断平行线才能执行此操作。特别是,如果在图中查看L7,它看起来与我们所认为的欧几里得线都是不一样的。我的想法与我一直在思考的“结作为流程”方面有很多直接关系,我认为线条将成为流程。Fano平面将会成为线的平行组合,但是这些点将会成为一组redex。它们将成为线之间相互作用的方式。
请查看此图,我已对其进行了颜色编码。如果你查看该图,就会看到L1,L3和L4应该能够在0.1处相互作用。我们看到的就是如此。这些行中的括号代表潜在的交互作用。遵循编码很简单。但是对于编码,我所做的是在交互继续时使其抽象化。L1有一个paren,它在X13上交互,在X3上等待,调用从Y13得到的东西,然后变成P13。总体来说,这是对X14上所发生情况的一个总结。
有趣的一点是,如果让RN返回自身,则此编码将保持稳定。
Christian: 让什么返回自身?
Greg: 如果使P13基本为该总和。做一个递归。到处都有续行,必须递归。输出也是一样操作。为了保持稳定,必须将它们撞开。
Christian: 你说稳定,这是什么意思?
Greg: 否则它就会演化成非Fano平面的东西。
Christian: 哦,对。
Isaac: 你的意思是说,如果要进行减容或其他操作,则只有在进行这些继续操作后,才能返回至Fano平面。在你特别提到过的表达式中,P13和P14都必须是那个选择表达式吗?
Greg: 它们都必须是那个选择表达式。
Isaac: 这就说得通了。
Greg: 这立刻会引发一种可能性,就是它们会无法返回。它们会变成其他东西。然后,这就会引出所有这些奇妙的区别。可以想象一下,无论进化如何,总会获得一种连续性的概念,即总会得到一种几何形状的东西。你必须得说出什么是几何。例如,这是一组具有点和线的重合关系的点和线。你所得到的总是几何图形。现在,我们很容易能想象出它演变成非几何形状的东西,例如非重合关系。
Christian: 你说的是,是否可以将任意并行进程编码为其中之一……
Greg: 几何。
Christian: 你说在什么情况下这是有可能的?
Greg: 就像它们在这里所做的一样,只要你有一组看起来像线条的paren和一组与这些点匹配并符合重合关系的redex,就有可能。
Christian: 如果它们不互动,就没有互动的潜力。就像平行线一样。
Greg: 没错。隔离就类似于在欧几里德空间中的平行。
Christian: 输入与输出是由什么所决定的呢。仅仅是为了使交互潜力匹配吗?
Greg: 许多不同的编码都遵循相同的重合关系。事实上,我想指出一个有趣的地方:我使用了混合求和。实际上,我们可以查看不同种类的线。在某些行中,你需要进行统一的汇总。可以将仅输入或仅输出的行与混合后的行(例如L7)区分开。
我记不清了,但是我可以肯定地说,你可以证明如果不用混合求和,你是无法对Fano平面进行编码的。我认为这是一个相当简单的证明过程。我记不清为了得到这个结论所要采取的步骤,但我可以肯定地说,我得出的结论是必须使用混合求和。
这说起来很有趣,因为该定理的意思是你无法将混合求和的par保留编码保留为同步,也不能保留为仅受输入保护或未混合的保留。要对Fano平面进行编码就必须要有一个表现力跳跃。这很有趣。
你可以使用编码进行观察,再加上Christian你所观察到的,也就是在并行性与交互或隔离之间存在着某种相似之处。你可以根据它们所支持的交互类型来对这些行进行分类。你会看到,不同的几何会要求演算中具有某些特定类型的表达特性。这当中有很多探索机会,而你现在可以使用双仿真——这是一种非常强大的证明技术——对几何进行推理。
Christian: 我试图描述此处的交互作用是如何导致图形演变的。例如,如果L1与红色L3进行通信,那么图形将会如何变化呢?
Greg: 假设你选择了X13 Q13输出,那么也就是选择了X13 Y13 P13输入。如果P13不退还你所得到的,那么你也将不再拥有L1或L3。
Christian: 但你仍然拥有一部分……
Greg: 你有其中的一部分,但你没有线。
Christian: 这样一来三角形的整个部分就都消失了。
Greg: 没错。我们已经谈论过稳定性了——稳定性就是你会在演化时回到Fano平面。然后我们又讨论了连续性:你会在演化时回到几何图形。然后就有了另一个概念。人们在考虑弦理论时实际上已经想到了这一点。你可以进行一些演化,它会将你从几何事物中带走,然后最终又回归到几何事物中。这简直是奇迹。你会经历一个水变酒的时期,然后再回到正常世界。这对我来说也很有趣。在弦理论中,他们考虑了时空撕裂的可能性。
Isaac: 这听起来像是奇点。
Greg: 正是如此。你可以考虑这些几何形状——用“支持”来形容可能不错——但你可能可以从中推出奇点的概念。这是此演示的另一个有趣之处。从我的角度来看,这表明了我们对如何使用此类型计算技术几乎完全没有了解,这些过程计算的力量还有待探索。我们还没有真正考虑过如何使用这些小工具。
它们非常强大,但我们对它们知之甚少。我们可以通过这种方式进行编码。特别是,重要的是(我后面会继续讨论)在计算上它是完整的。它具有一定的最低表达水平。这是组成性的。这真的很重要,因为它意味着你可以进行块状推理,而不必一次性考虑整个系统,这是物理学和许多经典数学所面临的最大挑战之一。这不是组成性的,所以你必须拥有全局观或上帝之眼,这就使得问题解决变得异常困难,并且使物理理论难以检验。
Christian: 关于这种编码的一般形式,你有什么著作吗?
Greg: 我在许多不同的论文中都提到了这一点,但还从未写过一篇专门针对编码和图形的论文。这主要是因为我开发了专用于图形的TOGL理论。例如,我们可以证明每个TOGL表达式在Rho演算中都有一个编码。这就是这些图形编码技术的一种体现方式。
我们也可以这么思考一下:在无限几何的情况下,它会如何变化? Fano平面的有限性有助于使它更容易处理,七个点和七个线。写起来很容易,但一旦获得这些无限结构,过程演算的表达能力又会怎样变化呢?
Isaac: 我第一次在Casper分享系列看到这些东西时并没有注意到这一点。凭直觉,第1、2和3行在某种程度上确实很相似。它们都位于三角形的外侧。它们的编码都非常相似——无混合求和。所有在该中点相交的线(线4、5和6)也都具有非常相似的编码,并具有一个混合求和。然后,在第7行,连接所有这些中点的圆也具有不同的编码,它们都是混合求和。我觉得很有趣,你发现了这些行本身的属性,以及它们与编码中的其他行相似的事实。
Greg: 当我构建编码时我就想到了——我试图确保编码的形状遵守几何中似乎正在发生的情况。我承认,我没有探索多种替代编码来确认这种区别是否总是出现,因为很明显,编码应该遵循这种区别。我选择了一种使其尽可能明显的编码。
我认为类型系统从这里开始变得真正有趣起来了,我们可以在类型级别上挑选出这类现象。然后,我们将会得到一个透镜。也许还会有外部三角形,但是内部的东西开始变得更有趣或更复杂起来了。你可以得到一些能够描述边界的类型,但对中间发生了什么则较少区分。然后,你将得到许多几何形状。或者你也可以反过来:丢弃内部的类型,而不是边界。
对我来说,这很棒很酷,它表明了我们对过程代数所能体现的东西知之甚少。当然,我们也可以探讨一下协议,拓扑,或者几何。我们能从中得到多少?我真的很希望能激发下一代的人们去研究这些问题。艺术无涯,而生有涯。
Christian: 这和你之前谈到的图语言理论之间存在联系吗?
Greg: 这就是我所说的TOGL:图形理论。
Christian: 哦,对。
Greg: 我可以使用一个TOGL表达式,它会提供一个图形,并使用此技术对其进行编码。由于这确实是一种理论,所以你可以说它们是该理论的模型。实际上,你可以通过这种方式开发出一整个有趣的理论模型结构。实际上,对它使用LADL(逻辑作为分配法则)可能会很有趣。可以将LADL应用于理论,也可以将LADL应用于模型。然后,你必须对从理论获得的类型到模型获得的类型进行态射。同样,这也是一件很有趣的事情。
Christian: 绝对是。
Greg: 你上次报告的工作进展如何,Christian?
Christian: 一切顺利,就剩下写论文了;这可能会是一系列论文。最有趣的问题在于,我们通过此方法可以表达出多少内容?我已经弄清楚如何在此设置中进行递归。基本上可以采用Rho演算理论。大体上来说,你要将每个基本类型排序发送到子功能单元格(如果可以表示的话)。因此,对于理论中的每种类型,你都会得到一个隐藏代数,而你要找出隐藏代数类别中的原始理论。尤其是类别。它们是笛卡尔封闭的球型,还有一些其他不错的东西。尤其是,你所获得的结果将不仅仅是原始理论,还伴随着某些操作。
具体来说,你可以考虑隐藏代数上的自函子。例如,如果有一个带有自由排序进程变量的进程,那么这就是一个仿函子,从进程格回到其自身(因为它接受一个进程并将其插入到该自由变量中),对于任何自函子而言,你始终可以采用该自函子的初始代数。对于任何带有自由变量的过程,当你想说mu ex进行递归时,你就是在形成该自函子的初始代数。
Greg: 我明白。通常来说,你不仅要对流程进行递归,还要对公式进行递归。你想描述的是递归公式。
Christian: 这正是我想说的意思。您可以通过自由变量得到任何谓词——自由变量也是类型进程谓词,而不仅仅是一个过程。
Greg: 明白了。
Christian: 我们可以从名称空间逻辑中获取所有信息,甚至看来可能还能得到更多,问题是到底是多少。用这种方法可以表达什么,不能表达什么,这可能是尚待确定的主要问题。
Greg: 这真的很棒。你有告诉John Baez有关这项工作的事吗?
Christian: 是的。他很喜欢这个点子。他要强调的重点是,这将成为某种中间逻辑;我们还不清楚它到底能表达多少。他告诉我,我需要确认这一点。
Greg: 哦,好的。非常好。
Christian: 我很高兴能够与你见面并讨论如何实施这些内容。
Greg: 是的,我也是。我越来越感觉到Agda缺少一些关键要素。如果要使用类型系统进行与术语形状相关的某些属性的验证的话,就必须进行反射。你需要在“我有一个作为数据结构的术语”和“我有一个作为可以检查其结构的编译器的术语”之间来回进行。看起来Scala比Agda更好。我会继续思考,但这就是我目前对于实施的想法。
Greg: 使用那些语言来写演算理论是一件简单的事情吗?
Greg: 我用Scala做出了多个基本实施,我所做的是用这个类型系统来验证理论是否正确,因为编译器说:“是的,这是一个类型,并且该术语符合该类型。”至少我们知道这并非无关紧要。类型是内置的。我已经提供了许多实施方案,并且已经对那些尝试提出各种实施方案的人员进行了培训。实际上,那是RChain生态系统中的一部分,但它可能会给人们造成一些困惑。
RChain微博:RChain官方
RChain官网:https://rchain.coop/
RChain代码库:https://github.com/rchain
Rholang编程语言学习:
https://github.com/JoshOrndorff/LearnRholangByExample/blob/master/README_CN.md
Rholang交流QQ群:788367740