这篇介绍如何求约束问题的解。涉及到很多高等数学和线性代数的知识。
建议先读:支持向量机 数学推导Part1
最优分离超平面的优化问题
上一篇文章的最后我们发现要求最优分离超平面等价于求W最小的模。求这个模需要解决一个优化问题:
最小化在(w,b)(w,b)中的∥w∥‖w‖, 服从 yi(w⋅xi+b)≥1yi(w⋅xi+b)≥1 , i=1,…,ni=1,…,n。
这个优化问题有n个约束。在解决难题之前,先介绍如何解决无约束条件最小化问题。
无约束条件最小化问题
极值定理:
函数在定义域内有连续的二阶导数,当一阶导数为0,二阶导数大于零时,在该点取得极小值。
深入定理
ff 在x∗x∗处梯度为零, 可以表示为 ∇f(x∗)=0∇f(x∗)=0,
函数 ff 在x∗x∗处的二阶导数大于零,可以用矩阵的形式可以表示为 z⊺((∇2f(x∗))z>0,∀z∈Rnz⊺((∇2f(x∗))z>0,∀z∈Rn,其中二阶偏导数为
维基百科-海森矩阵
海森矩阵(Hessian matrix 或 Hessian)是一个多变量实值函数的二阶偏导数组成的方块矩阵,所以上面的二阶偏导数也就是海森矩阵。
二维情况下
给定二阶导数连续的映射f:R2→Rf:R2→R,海森矩阵的行列式,可用于分辨ff的临界点是属于鞍点还是极值点。
- H > 0:若∂2f∂x2>0∂2f∂x2>0,则(x0,y0)(x0,y0) 是局部极小点;若 ∂2f∂x2<0∂2f∂x2<0,则 (x0,y0)(x0,y0)是局部极大点。
- H < 0: (x0,y0)(x0,y0) 是鞍点。
- H = 0:二阶导数无法判断该临界点的性质,得从更高阶的导数以泰勒公式考虑.
高维情况下
当函数f:Rn→Rf:Rn→R二阶连续可导时,Hessian矩阵H在临界点x0x0上是一个n×nn×n阶的对称矩阵。这也是一个定理,下面会用到。
- 当H是正定矩阵时,临界点x0x0是一个局部的极小值。
- 当H是负定矩阵时,临界点 x0x0是一个局部的极大值。
- H=0,需要更高阶的导数来帮助判断。
- 在其余情况下,临界点 x0x0不是局部极值。
正定矩阵
我们想要寻找函数在某点处的值是不是极小值,在高维情况下,只要海森矩阵是正定矩阵,那么就能够得到在这个点处取得极小值。
正定矩阵定义: 如果一个x⊺Ax>0x⊺Ax>0,那么对称矩阵A是正定矩阵。
正定有两个条件:1)矩阵A是对称矩阵 2)存在一个可逆变换xx使得x⊺Ax>0x⊺Ax>0。
上面说到,具有连续二阶偏导数的函数,其海森矩阵是对称矩阵。定义中的x⊺Ax>0x⊺Ax>0换成我们的表达式就是 z⊺((∇2f(x∗))z>0,∀z∈Rnz⊺((∇2f(x∗))z>0,∀z∈Rn中,如何确定zz呢?这个通常是很困难的。我们通常用以下定理来证明一个对称矩阵是正定矩阵。
- 所有特征值大于0
- 所有余子式大于0
- 存在非奇异方阵B,使得A=B⊺BA=B⊺B
例子
寻找 Rosenbrock’s banana function: f(x,y)=(2−x)2+100(y−x2)2f(x,y)=(2−x)2+100(y−x2)2的最小值。
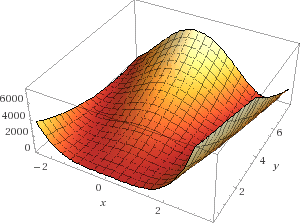
1)求一阶偏导数
2) 求海森矩阵(所有二阶偏导数和二阶导数)
代入 (x,y)=(2,4)(x,y)=(2,4)计算得
3)判断其是否为正定矩阵。
首先,这个海森矩阵是对称矩阵,接着就要看他满不满足上面说的三个定理中的任意一个。阶数低的情况下比较好求,这里通过余子式就能看出来。
如何求最小值
上面求了半天只求了局部极小值。
局部极小值并不一定是最小值,极大值也不一定大于极小值,可以通过求出所有的极值,选择其中最小的就是最小值。
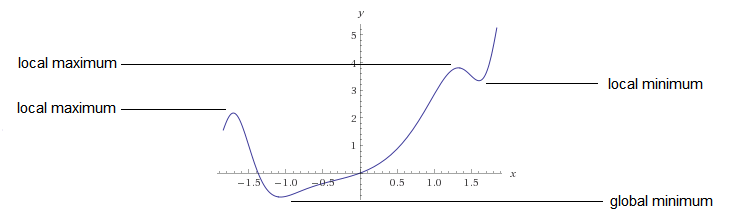
这是支持向量机数学推导的部分,下面讲的是凸函数。
先回顾一下问题,如何求全局的最小值?
前面的讨论我们说可以把每一个极值点求出来再一个个对比,取最小的那个就是最小值。
另外的一个方法就是学习我们想要最小化的函数是怎样的函数。如果一个函数是凸函数,那么我们就能确定局部最小值就是全局的最小值。
凸函数(Convex functions)
如果能够在函数中找到两点画一条直线,这条直线不与函数的第三个点相交,那么这个函数就是一个凸函数。
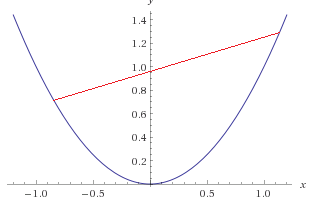
凸函数
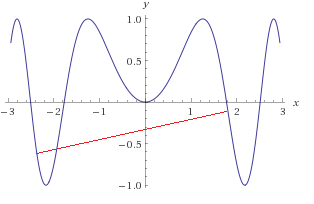
非凸函数
但是从上面的非凸函数中,我们也能找到在区间[-1,1]内,函数是凸函数。
凸函数函数的另外一种形式,凹函数(concave function)
数学中的定义:
A function is convex if its epigraph (the set of points on or above the graph of the function) is a convex set.
什么是凸集(convex set)?
维基百科:
在点集拓扑学与欧几里得空间中,凸集(convex set)是一个点集合,其中每两点之间的直线点都落在该点集合中。
几个例子

我们看到星型两个点之间的连线有一部分没有落在它的集合中,所以不是凸集,而圆和三角形则是凸集。
怎么求一个函数是凸函数?
对于二维的函数用图示的方法很好理解,但是对于多个变量的高维函数,要将它的图形画出来可没有那么容易。所以先学习函数,看看函数有什么特点。
凸函数的性质:多元二次可微的连续函数在凸集上是凸的,当且仅当它的海森矩阵在凸集的内部是半正定的。
因此,想要证明我们的函数是凸函数,只需要证明海森矩阵是半正定的就可以, 可以通过以下定理证明.
对称矩阵A是半正定矩阵等价于:
- 矩阵A的全部特征值非负;
- 矩阵A的所有主子式(principal minors)非负;
- 存在BB使得A=BTBA=BTB.
与证明海森矩阵是正定矩阵唯一的不同就是,这里证明所有主子式非负。
例子: 香蕉函数是凸函数吗?
香蕉函数的海森矩阵:
主子式 M11M11为 200200, M22M22为 1200x2−400y+21200x2−400y+2
如果这个函数是一个凸集,那么我们需要证明从任何点得到的所有主子式都是非负的。
M22M22不满足,当取点(1,4),M22=−399M22=−399.
所以香蕉函数不是凸函数。
很多方法可以求一个函数是否为凸函数。这里不多介绍了。
为什么凸函数这么酷?
首先,局部最小值就是全局最小值;其次,凸函数优化问题容易解决。为什么呢?
为了更好理解,我们先看一些图:
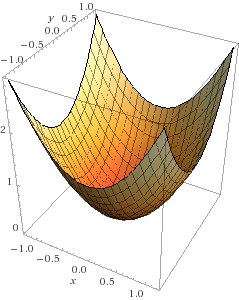
优化问题可以理解为扔一粒石子到一个平面。对于凸平面,像上面一幅图,无论你在哪里扔下石子,它会直接落到底部,也就是函数的最小值处。
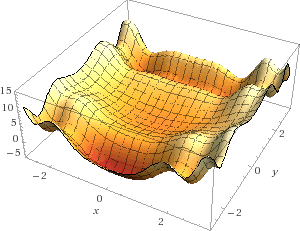
对于非凸平面,当我们随便扔下石子时,它更有可能落到局部最小值处而不是全局最小处。要使石子落到最小值处就变得十分复杂。
梯度下降优化算法就像是让石子找到最小值的过程,另外牛顿方法也是著名的优化问题解决方法。
总结
这篇文章介绍了什么是凸集以及怎么证明一个函数是凸集。
在解决优化问题时,凸面是一个需要理解带的重要的概念。另外一个重要的方面是二元性。
才疏学浅,还未能创造知识,先做知识的搬运工!
原文地址:https://www.svm-tutorial.com/2016/09/convex-functions/