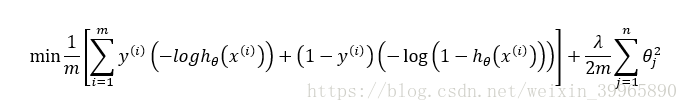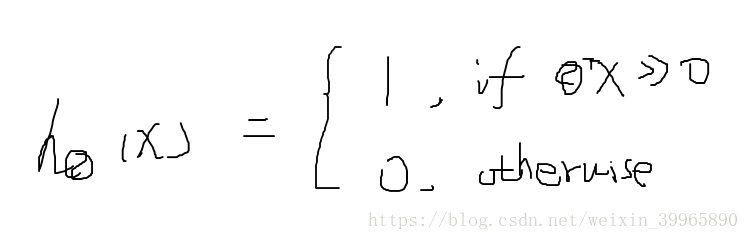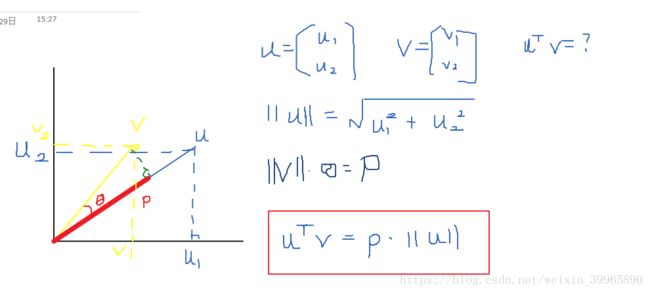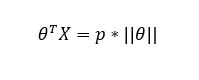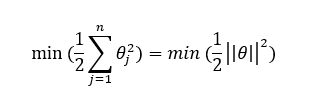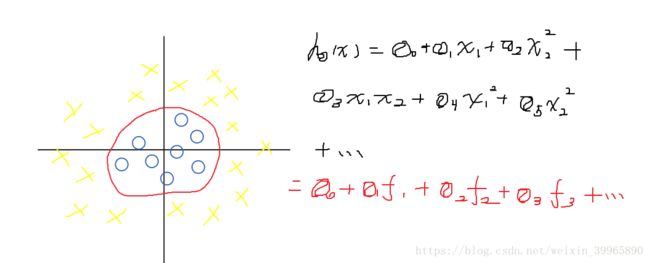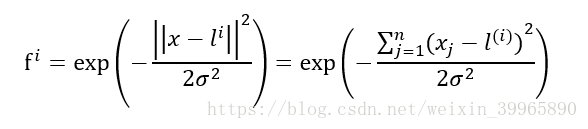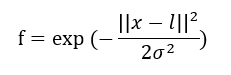支持向量机【Coursera 斯坦福 机器学习】
本文基于coursera 斯坦福 吴恩达机器学习课程
谢绝任何不标注出处的转载以及百度百家号抄袭
如有问题请联系作者
很多监督学习的效果都非常相似。支持向量机(Support Vector Machines, SVM)就是其中一种很强大的监督学习。
1. SVM V.S. Logistic Regression
SVM的定义可以和逻辑回归类比着看。
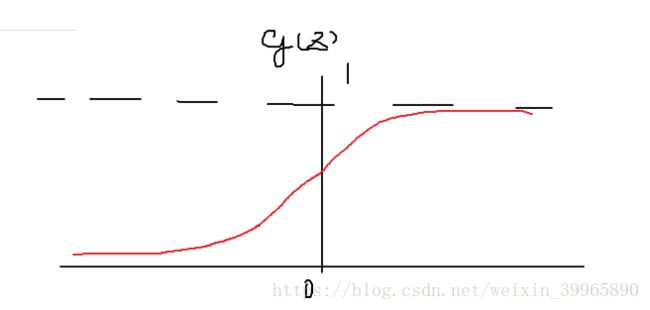
首先复习一下逻辑回归。逻辑回归和线性回归假设对比如下所示,逻辑回归常用函数为sigmoid。
下图为sigmoid函数。
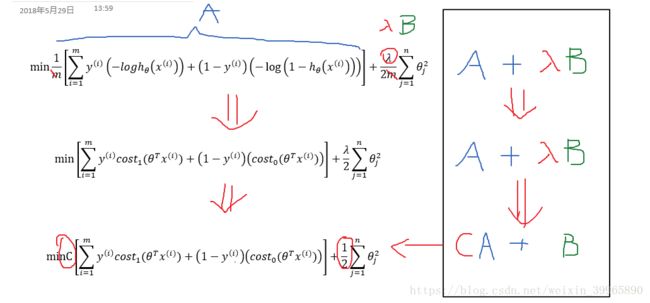
对于逻辑回归,我们有cost function:
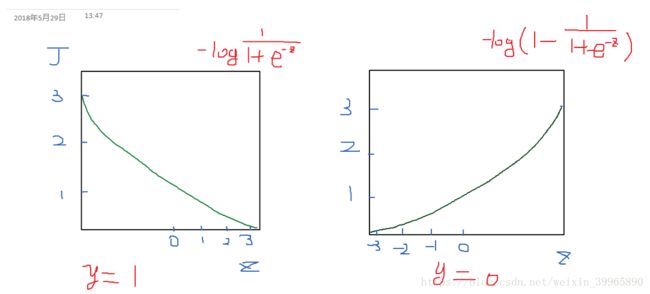
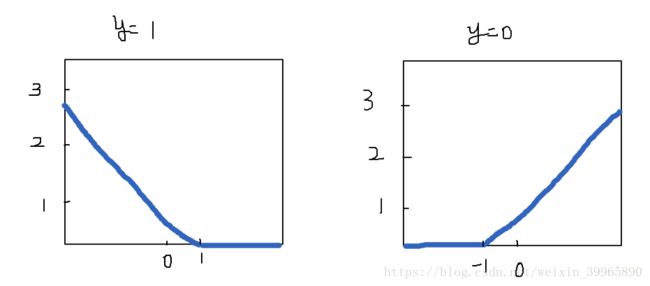
其中,当y分别为1和0时,cost function(无正则化)函数图像为(h为sigmoid):
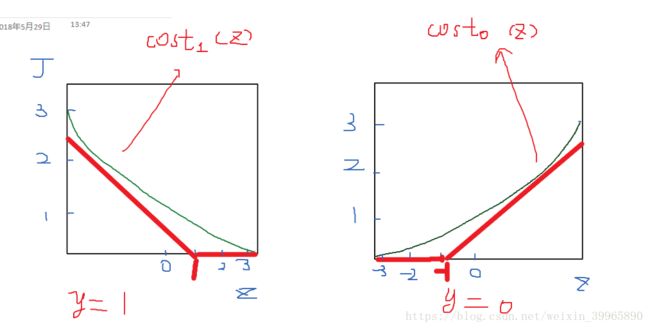
对于SVM,我们将此cost function图像改变为下图红色粗线所示。分别给两个函数命名为cost0(z)和cost1(z),角标即为y值。
那么我们有新的cost function。首先,我们去掉m得到第二行的公式。然后需要一个思想的转换:逻辑回归中,我们用正则化系数λ控制惩罚度,SVM我们使用一个C来控制基础的cost function, 以此达到类似正则化的效果。最终带正则化的cost function为第三行公式。当C=1/λ时,两个cost function结果相同;此时,如果C很大(即λ很小),我们会面临low bias, high variance问题;反之,是high bias, low variance。
综上,我们得到SVM的假设:
2. Large Margin & Linear Descision Boundaries
2.1 向量内积
我们有向量u和v, 那么可以得到v在u上的映射为p, 则有: u^T*v = p * ||u||,其中,||u||为向量u的长度。
推导过程如下:
如此一来,θ^T*X就可以被写为如下公式,p为向量X投影到θ上的内积(标量,有正负值)。
2.2 SVM margin
对于SVM的cost function,我们有():
如下图所示,当y=1时,我们希望θ^T*x可以大于1(使得cost1为0);当y=0时,我们希望θ^T*x可以小于-1. 如此一来,A项为0,我们只需要最小化B即可。
根据2.1向量内积的知识,θ^T*X = p * ||θ||,且可以把B写作:
当y=1, 我们希望p * ||θ|| > 1;当y=0, 我们希望p * ||θ|| < -1.
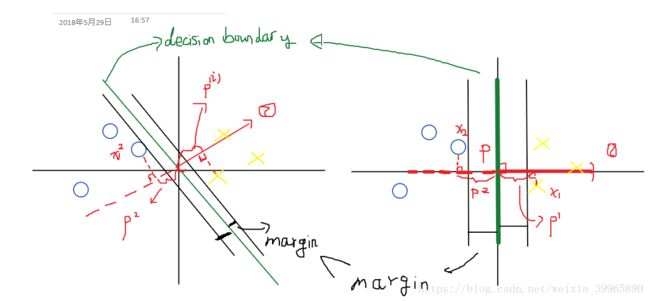
现在举一个例子来说明这两个不等式和B项的关系。首先方便起见,我们假设θ0 = 0。如下图所示,两个类别中的数据离SVM descision boundary最近的距离被称为margin。左图的margin明显小于右图。通常,SVM会倾向于选择margin大的decision boundary。
原理如下:θ向量是decision boundary的转置,所以θ和decision boundary是垂直关系,作图可以得知:左图的p(由数据点x到θ向量的投影)会小于右图的p。当y=1时,为了确保θ^T*X = p * ||θ||>1,p越小,||θ||需要越大;当y = 0时,p为负值,为了确保θ^T*X = p * ||θ||<-1,p越小,||θ||需要越大。而我们cost function的初衷就是最小化θ,所以我们需要大的p值。这也是为什么SVM会选择margin大的decision boundary.
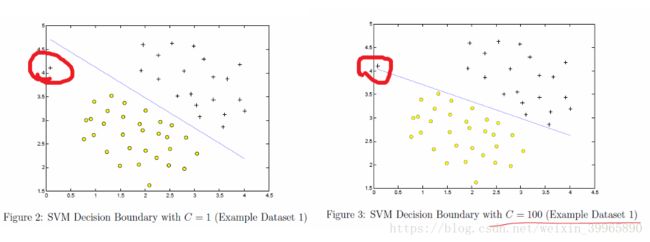
以上例子是建立在θ0=0的特例上的,对于普通情况依然适用。这里需要注意一个小问题,当C十分大时,decision boundary很容易受到outlier的影响;反之,decision boundary对outlier不敏感。如下图所示。
此外,其实在编程中B项的θ^2是被写作θ^T*M*θ的,M是一个矩阵,这里没有太明白。
3. Kernels & Non-linear Decision Boundaries
这里依然用例子说明。如下图所示,我们有如下decision boundary和hypothesis。可以看到,我们的hypothesis是由x1和x2组成的函数,那么就可以改写成红色的函数。其中f1, f2, ...是由x1和x2构成的函数。我们期望所有的蓝圈都能被x1和x2表示为一类,所有的黄叉被表示为另一类,所以我们要在f上做文章。
对于每个f,我们有:
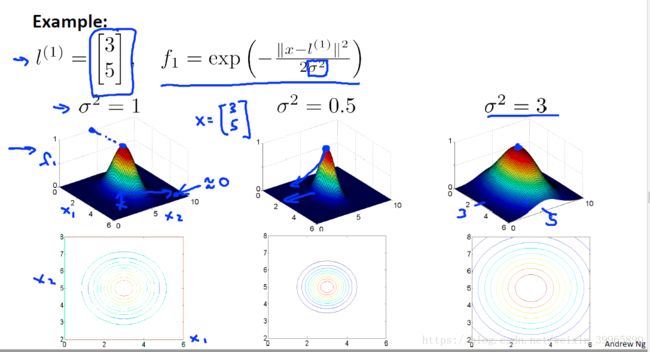
其中,i为第i个函数; exp为similarity(即kernel)的一种,被称作Gussian Kernels; j为第j个数据点;σ为参数,用来决定"how fast the similarity metric decreases (to 0)"。当σ很大时,f会比较smooth,拥有high bias, low variance; 当σ小时,f会比较sharp,low bias, high variance。l为由x1和x2组成的坐标轴上的点(landmarks)。
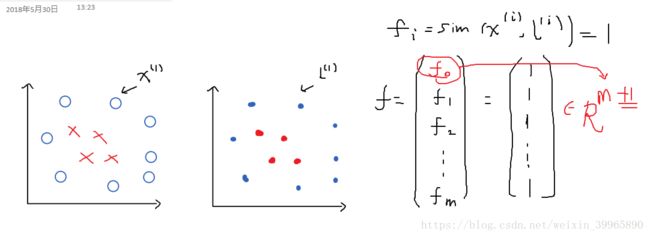
那么如何选择landmark呢?我们会将每一个数据点的位置赋值一个landmark, 如下图所示。从上图公式中可知,若x与l(i)很相似,fi接近于exp(0)=1. 若x与l(i)差值越大,fi越接近于0。因为x和l一模一样,所以每个f的值都为1, 为了补位,我们加上了f0(恒为1),所有小f构成了一个m+1长度的f向量,用于θ^T*f的计算。
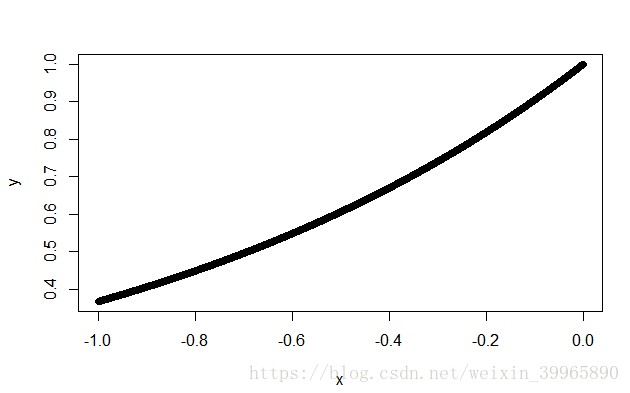
下图是一个用来看exp()函数的plot。
下图为课程中给出的不同σ的例子:
由f的公式可知,每一个f都对应着一个l,当h用f表示时,其实也是h被l以某种形式呈现出来。那么对于x1,x2构成的关于l的图像,我们就有:
这里是有点绕的。我们用每一个x与某一个landmark的“相似度”(similarity)的平方和来衡量f应该为0还是1;然后再通过每一个f得到的值放入h中,得到估计值为1的landmarks的分布。
4. 使用SVM与kernel的选择
现在SVM有很多包,主要需要我们选择的就是C和kernel (similarity function)。很多SVM包已经能直接操作multi-classification 问题了。除此之外,可以使用one-vs-all mehtod。
对于kernel的选择,有如下方案:
(1)no kernel (linear kernel):当θ^T*xi≥0时,估计值为1。如果feature的数量n很大,训练集数据量m很小,那么我们可以选择这种方法。此时,也可以直接使用逻辑回归。如果n十分小,m非常大(例如n与m相差50倍等),也可以用无kernel的SVM或逻辑回归。这也说明,没有kernel的SVM和逻辑回归十分相似。
这里我们需要选择σ。如果n小m一般大,可以用这种方法。在使用Gaussian kernel之前一定要做feature scaling.
(3)other kernels: 这里需要注意的是,并不是所有的similarity functions都能产生有效的kernel(需要满足一个叫“Mercer's Theorem”的东西)。可用的kernel有:
a. polynomial kernel: k(x, l) = (x^T*l)^2, (x^T*l)^3, (x^T*l +1)^3, ...多项式kernel的主要参数为加在x^T*l后的常数和其degree(有一点像GAM里面的polynomial splines啊)。polynomial kernel不是很常用。
b. String kernel
c. chi-square kernel
d. histogram intersection kernel, ...
这些都是极少用到的。
在选择参数和kernel时,我们只选择在CV 数据集中表现最好的那个。
对于(1)和(2)提到的m和n的不同情况,神经网络都能兼容并且做的不错,就是建模可能会慢一些。
最后复习一点,逻辑回归的cost function是convex凸面的,所以梯度下降只会返回global optimal。