SVM机器学习实战2(包含训练数据)
上一篇简单的用sklearn里面的SVM训练数据,本次按照机器学习实战里面的简易版的SMO来训练数据。
详细代码如下:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.utils import check_random_state
from sklearn import datasets
#load data
def loadData():
iris = datasets.load_iris()
rng = check_random_state(42)
perm = rng.permutation(iris.target.size)
iris_data = iris.data[perm]
data = []
for i in iris_data:
data.append(i[:2])#选择前两个特征作为本次训练的基本特征
iris_target = iris.target[perm]
#将label分为+1('Iris-setosa') 和 -1('Iris-versicolor'和'Iris-virginica')
iris_target = np.where((iris_target == 1) |(iris_target == 2), -1, 1)
return data, iris_target
#随机选择一个alpha
def selectJrand(i, m):
j = i
while j == i:
j = int(np.random.uniform(0, m))
return j
#调整大于H或小于L的alpha 值
def clipAlpha(aj, H, L):
if aj > H:
aj = H
if aj < L:
aj = L
return aj
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
dataMatrix = np.mat(dataMatIn)
labelMat = np.mat(classLabels).transpose()
b = 0
m, n = dataMatrix.shape
alphas = np.mat(np.zeros((m, 1)))
Iter = 0
while Iter < maxIter:
alphaPairsChanged = 0
for i in range(m):
# y = wx + b, w = αyx 具体的推导过程见周志华的西瓜书
fXi = float(np.multiply(alphas, labelMat).T * dataMatrix * dataMatrix[i, :].T) + b
Ei = fXi - float(labelMat[i])
# 判断α是否满足KTT条件
if ((labelMat[i] * Ei < -toler) and (alphas[i] < C)) or ((labelMat[i] * Ei > toler) and (alphas[i] > 0)):
j = selectJrand(i, m) #随机选择另外一个数据向量
fXj = float(np.multiply(alphas, labelMat).T * dataMatrix * dataMatrix[j, :].T) + b
Ej = fXj - float(labelMat[j])
alphaIold = alphas[i].copy()
alphaJold = alphas[j].copy()
if labelMat[i] != labelMat[j]:
L = max(0, alphas[j] - alphas[i])
H = min(C, C + alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C, alphas[j] + alphas[i])
if L == H:
print ("L == H")
continue
#保证alpha在0与C之间, eta是alpha[j]的最优修改量
eta = 2.0 * dataMatrix[i, :] * dataMatrix[j, :].T \
- dataMatrix[i, :] * dataMatrix[i, :].T \
- dataMatrix[j, :] * dataMatrix[j, :].T
if eta >= 0:
print ("eta >= 0")
continue
###对i进行修改,修改量与j相同,但是方向相反
alphas[j] -= labelMat[j] * (Ei - Ej) / eta
alphas[j] = clipAlpha(alphas[j], H, L)
if abs(alphas[j] - alphaJold) < 0.00001:
print ("j not moving enough")
continue
alphas[i] += labelMat[j] * labelMat[i] * (alphaJold - alphas[j])
b1 = b - Ei \
- labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[i, :].T \
- labelMat[j] * (alphas[j] - alphaJold) * dataMatrix[j, :] * dataMatrix[i, :].T
b2 = b - Ej \
- labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[j, :].T \
- labelMat[j] * (alphas[j] - alphaJold) * dataMatrix[j, :] * dataMatrix[j, :].T
if 0 < alphas[i] < C:
b = b1
elif 0 < alphas[j] < C:
b = b2
else:
b = (b1 + b2) / 2.0
alphaPairsChanged += 1
print ("iter: %d i:%d, pairs changed %d" % (Iter, i, alphaPairsChanged))
if alphaPairsChanged == 0:
Iter += 1
else:
Iter = 0
print ("iteration number: %d" % Iter)
return b, alphas
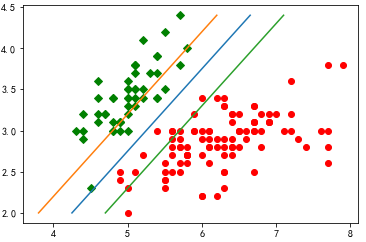
#画图
def show(dataArr, labelArr, alphas, b):
for i in range(len(labelArr)):
if labelArr[i] == -1:
plt.plot(dataArr[i][0], dataArr[i][1], 'or')
elif labelArr[i] == 1:
plt.plot(dataArr[i][0], dataArr[i][1], 'Dg')
c = np.sum(np.multiply(np.multiply(alphas.T, np.mat(labelArr)), np.mat(dataArr).T), axis=1)
minY = min(m[1] for m in dataArr)
maxY = max(m[1] for m in dataArr)
print (minY, maxY)
#支持向量
plt.plot([np.sum((- b - c[1] * minY) / c[0]), np.sum((- b - c[1] * maxY) / c[0])], [minY, maxY])
plt.plot([np.sum((- b + 1 - c[1] * minY) / c[0]), np.sum((- b + 1 - c[1] * maxY) / c[0])], [minY, maxY])
plt.plot([np.sum((- b - 1 - c[1] * minY) / c[0]), np.sum((- b - 1 - c[1] * maxY) / c[0])], [minY, maxY])
plt.show()
# 测试
data , label = loadData()
b, alpha = smoSimple(data, label, 0.6, 0.001, 40)
alpha[alpha>0]
show(data, label, alpha, b)