数学--数论--整除分块（巨TM详细，学不会，你来打我）

1.概念
从一道例题说起
$在介绍整除分块之前，我们先来看一道算数题：已知正整数n，求\sum i=1n\lfloor ni\rfloor \begin{array}{r}已知正整数n，求\sum _{i=1}^n\lfloor \frac{n}{i}\rfloor \end{array}$

我们写一个表格看一看1-20的整除是什么样子的

i	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
$\lfloor \frac{20}{i}\rfloor$	20	10	6	5	4	3	2	2	2	2	1	1	1	1	1	1	1	1	1	1

表中同样的值会连续出现，而相同的值所划分的区间积是整出分块。整除的性质使得从1到n的数组表可根据数值划分为不同的分块，且分块数远远小于n。利用这种性质，我们如果能推导出每个分块具体的左右端点位置在哪，这个问题就可以快速求解出来了。

2.整除分块公式推导

向下取整的情形
还是说我们的例题
$已知正整数n，求{\sum }_{i=1}^n\lfloor \frac{n}{i}\rfloor$
 假设我们已知某一个分块的左端点lll，要求解出该分块的右端点rrr。设该分块的数值为kkk，对于该分块中的每个数iii，有$k=\lfloor \frac{n}{i}\rfloor =\lfloor \frac{n}{l}\rfloor$，即$ik\le n$，也就是说我们找到可得使$ik\le n$成立的最大的i的值即是我们所求的右端点r，因此我们可以得到下列式子:

$\{\begin{array}{l}k=\lfloor \frac{n}{l}\rfloor \\ \\ r=\max (i),ik\le n\end{array}$

推导可得：

$r=\lfloor \frac{n}{k}\rfloor =\lfloor \frac{n}{\lfloor \frac{n}{l}\rfloor }\rfloor$

容易得到代码：

ans = 0;
for(int l = 1, r; l <= n; l = r + 1)
{
    r = n / (n / l);
    ans += n / l * (r - l + 1);
}

But 还没有结束

我们再看这一道题：

$\begin{array}{r}已知正整数n,a,b,求\sum _{i=1}^n\lfloor \frac{n}{ai+b}\rfloor \end{array}$

抓瞎了，但是变变形应该可以做。

我们记得

$\{\begin{array}{l}k=\lfloor \frac{n}{l}\rfloor \\ \\ r=\max (i),ik\le n\end{array}$
$r=\lfloor \frac{n}{k}\rfloor =\lfloor \frac{n}{\lfloor \frac{n}{l}\rfloor }\rfloor$
以上两个公式，我们有如下
$\{\begin{array}{l}k=\lfloor \frac{n}{al+b}\rfloor \\ \\ r=\max (i),(ai+b)k\le n\end{array}$

上式子可推导为

但是对于这个题目，我们给出第二种推导方式，使得一种推导方式解决多种题目。

这我们再做
$\begin{array}{r}已知正整数n,求\sum _{i=1}^n\lfloor \frac{n}{i^2}\rfloor \end{array}$
我们按照上面的方式推导

不知道这时候有多少人偷笑，说自己把整除分块学会了，曾经以为自己是个王者，结果他爸来。

这个题你懵了吗，对于一对 L和R，中间的值是等差数列，相差1，归根结底还是整除分块，还是找到l和r，通过等差数列计算即可。
代码如下：

#include
using namespace std;
int main()
{
    long long n, k, ans = 0;
    long long left = 1, right, rest;
    scanf("%lld%lld", &n, &k);
    while (left <= n && left <= k) //求从1到min(n, k)内的总和
    {
        right = min(k / (k / left), n);	
        rest = k % left;
        ans += (rest + rest - (right - left) * (k / left)) * (right - left + 1) / 2;
        left = right + 1;
    }
    if (n > k)
    {
        ans += k * (n - k);
    }
    cout << ans;
}

王者你会了吗？
王者自信满满的说自己会了！

王者再看看这个题

$已知正整数n，求{\sum }_{i=1}^n\lceil \frac{n}{i}\rceil$

没4没4，我们就不推导向上取整了，这里只需要一个小转化，将向上取整转化为向下取整。
我们考虑没有整除的时候是不是就有
$\lceil \frac{n}{i}\rceil =\lfloor \frac{n}{i}\rfloor +1$ 如果整除的时候就相等了，那么我们只要不加1，我们加上$\frac{i-1}{i}$就可以避免这种情况，那么就可以转化为

通过上面向下取整的推到即可得到

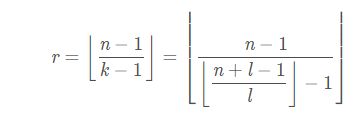
到这里王者就可以独当一面了。