图的最小生成树总结-java版

目录

最小生成树简介

最小生成树算法

Prim算法

Prim基本思想

Prim例子

Kruskal算法

Kruskal基本思想

Kruskal例子

java实现

基础代码

Prim算法

Kruskal算法

---

最小生成树简介

在一个任意连通图G中，如果取它的全部顶点和一部分边构成一个子图G'，即：V（G'）=V（G）和E（G'）⊆E（G）

若同时满足边集E（G'）中的所有边既能够使全部顶点连通而又不形成任何回路，则称子图G'是原图G的一棵生成树。

在一个连通图G=(V, E)中，对于其中的每条边(u,v)∈E，赋予其权重w(u, v)，则最小生成树问题就是要在G中找到一个连通图G中所有顶点的无环子集T⊆E，使得这个子集中所有边的权重之和w(T)最小。显然，T必然是一棵树，这样的树通常称为图G的生成树。
 

最小生成树算法

通常来说，要解决最小生成树问题，通常采用两种算法：Prim算法和Kruskal算法。先假设要求一个连通无向图G=(V, E)的最小生成树T，且以其中的一个顶点V1为T的根结点。下面就分别对这两种算法进行介绍。

Prim算法

Prim基本思想

Prim算法构建最小生成树的过程是：先构建一棵只包含根结点V1的树A，然后每次在连接树A结点和图G中树A以外的结点的所有边中，选取一条权重最小的边加入树A，直至树A覆盖图G中的所有结点。

计算最小生成树采用prim算法。在每一步，将节点当做根并往上加边，将相关顶点增加到增长的树上。在算法的每一个阶段都可以通过选择边（u,v）,使得（u,v）的值是所有u在树上但v不在树上的边的值的最小者，从而找到一个新的顶点并将它添加到这棵树中。

注意：在这个算法中，关键点在于在连接树A结点和图G中树A以外的结点的所有边中选取权重最小的边。

在算法实现过程中，要记录G中每个结点i到树A中结点的最小距离minidistance[i]（每个不再树A中的节点都有一个），以及与之相连的树A中的那个结点miniadj[i]（每个节点都保留两个值，到A中节点的min的边以及这条边的另一个顶点）。

minidistance[i]开始都初始化为无穷大，miniadj[i]都初始化为该顶点自己

每将一个结点j加入了树A，首先令minidistance[j]=0，

然后遍历图G中所有不在树A中的结点，看看往树A中加入了结点j后，这些结点到树A中结点的最小距离会不会变小，如果变小则进行调整。（其实就是看这些节点到j的距离，是否小于之前的距离，如果是，就换成到j的距离）

例如，对于结点k，它在图G中，但不在树A中，且结点k与结点j相连，该边的权重为w(k, j)。

在未将结点j加入树A前，结点k到树A中结点的最小距离为minidistance[k]；

将结点j加入树A后，如果minidistance[k] > w(k, j)，那么结点k到树A中结点的最小距离就是结点k到结点j的最小距离，所以要将minidistance[k]调整为w(k, j)，且miniadj[k]为j。

Prim例子

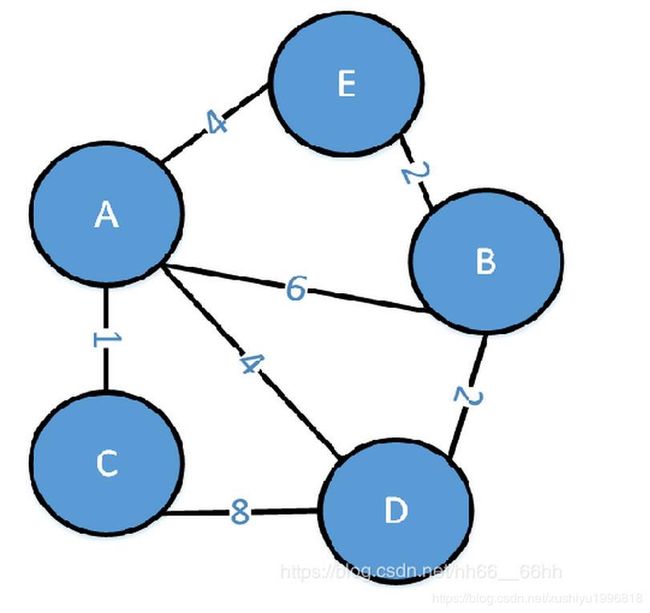
有一个无向连通图G，它有5个顶点，7条边，如下图所示。

以结点A最为根结点，利用Prim算法来生成该图的最小生成树T的过程如下：
（1）开始T为空，初始化minidistance[A] = minidistance[B] = minidistance[C] = minidistance[D] = minidistance[E] = ∞ {\infty}∞，miniadj[A] = A，miniadj[B] = B, miniadj[C] = C，miniadj[D] = D，miniadj[E] = E；

（2）将结点A加入T，这时minidistance[A] = 0，miniadj[A] = A， minidistance[B] = 6，miniadj[B] = A ，minidistance[C] = 1，miniadj[C] = A , minidistance[D] = 4，miniadj[D] = A , minidistance[E] = 4,miniadj[E] = A 。

（3）此时结点B,C,D,E都不在树T中，在连接树T结点和图G中树A以外的结点的所有边中，权重最小的边是minidistance[C]，且miniadj[C]=A，所以将结点C和结点C与结点A连成的边加入树T。此时，minidistance[A] = 0，miniadj[A] = A， minidistance[B] = 6，miniadj[B] = A ，minidistance[C] = 0，miniadj[C] = A , minidistance[D] = 4，miniadj[D] = A , minidistance[E] = 4,miniadj[E] = A 。

（4）此时结点B,D,E都不在树T中，在连接树T结点和图G中树A以外的结点的所有边中，权重最小的边是minidistance[D]和minidistance[E]，从中随便选一个，此处选结点D，且miniadj[D]=A，所以将结点D和结点D与结点A连成的边加入树T。此时，minidistance[A] = 0，miniadj[A] = A， minidistance[B] = 2，miniadj[B] = D ，minidistance[C] = 0，miniadj[C] = A , minidistance[D] = 0，miniadj[D] = A , minidistance[E] = 4,miniadj[E] = A 。

（5）此时结点B,E都不在树T中，在连接树T结点和图G中树A以外的结点的所有边中，权重最小的边是minidistance[B]，且miniadj[B]=D，所以将结点B和结点B与结点D连成的边加入树T。此时，minidistance[A] = 0，miniadj[A] = A， minidistance[B] = 0，miniadj[B] = D ，minidistance[C] = 0，miniadj[C] = A , minidistance[D] = 0，miniadj[D] = A , minidistance[E] = 2,miniadj[E] = B。

（6）此时只有结点E都不在树T中，因此在连接树T结点和图G中树A以外的结点的所有边中，权重最小的边是minidistance[E]，且miniadj[E]=B，所以将结点E和结点E与结点B连成的边加入树T，此时最小生成树构成，如下图所示：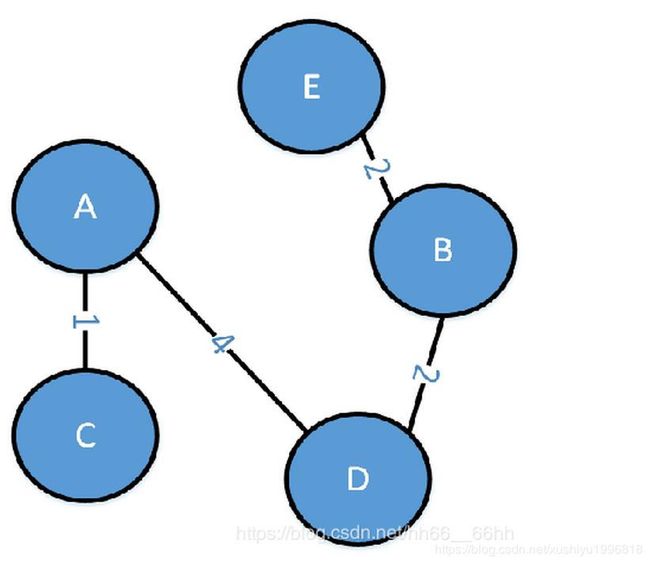

Kruskal算法

Kruskal基本思想

假设现在要求无向连通图G=(V, E)的最小生成树T，Kruskal算法的思想是

令T的初始状态为|V|个结点而无边的非连通图，T中的每个顶点自成一个连通分量（相当于本来有n个只有一个节点的树）。接着，每次从图G中所有两个端点落在不同连通分量的边中，选取权重最小的那条，（在不同的树间，选择一条联通两个树的权值最小的边，树的个数-1）将该边加入T中，如此往复，直至T中所有顶点都在同一个连通分量上。

和prim算法类似，每次都是寻找权值最短的一条边。可以这样看：开始存在n颗单节点树，每次找到权值最短的一棵树将其合并起来，但是注意不要形成环。最后只剩下一棵树的时候，代表合并完成。

注意
此处的关键点有两个：
（1）在生成最小生成树前，要对图中的所有边进行排序；
（2）如何判断一条边的两个端点是否落在不同的连通分量上：

这里可以用一个数组parent来记录每个端点在其所在连通图中的父端点（例如parent[i]表示端点i的父端点），在一个连通分量中，总有一个端点的父端点是它自己（把它看成是一棵树的根节点）。
1）开始的时候初始化该数组为parent[i]=i（因为每个端点所在的连通图只有自己）；
2）每次要判断一条边(u, v)的两个端点是否在在不同的连通分量上，就找端点u和端点v在它们所在的连通图中的最底层的父端点，具体的方法是递归地找端点k的父端点，直至某个端点的父端点等于它自己：
3）假设n=find_parent(u, parent)，m=find_parent(v, parent)，那么就要对它们进行判断：
如果n==m，说明结点u和结点v在一个连通分量上，因此不能将其加入T；
如果n!=m，说明结点u和结点v不在一个连通分量上，这时可以将(u,v)加入T，且令parent[n]=m（或parent[m]=n）。
（注意：这里的n和m是u和v的根节点，最后是为根节点设置父节点，而不是为边的两端设置父节点）

Kruskal例子

利用Prim算法来生成该图的最小生成树T的过程如下：
（1）先对图中的所有边按照权重递增的顺序排序：
(A, C, 1) , (B, D, 2) , (B, E, 2) , (A, D , 4) , (A, E , 4) , (A, B, 6) , (C, D, 8).
对每个端点的parent进行初始化：
parent[A] = A, parent[B] = B, parent[C] = C, parent[D] = D, parent[E] = E.

（2）从权重最短的边开始遍历：
1）(A, C, 1)，因为parent[A] != parent[C]，所以将边(A, C)加入树T，且令parent[parent[C]]=parent[A]=A.此时，parent[A] = A, parent[B] = B, parent[C] = A, parent[D] = D, parent[E] = E，此时T中有1条边。

2）(B, D, 2)，因为parent[B] != parent[D]，将边(B, D)加入树T，且令parent[parent[D]]=parent[B]=B.此时，parent[A] = A, parent[B] = B, parent[C] = A, parent[D] = B, parent[E] = E，此时T中有2条边.

3）(B, E, 2)，因为parent[B] != parent[E]，将边(B, E)加入树T，且令parent[parent[E]]=parent[B]=B.此时，parent[A] = A, parent[B] = B, parent[C] = A, parent[D] = B, parent[E] = B，此时T中有3条边

4）(A, D, 2)，因为parent[A] != parent[D]，将边(A, D)加入树T，且令parent[parent[D]]=parent[A]=A.此时，parent[A] = A, parent[B] = A, parent[C] = A, parent[D] = B, parent[E] = E，此时T中有4条边，正好等于端点数减一，因此树T生成。
 

java实现

基础代码

图的基础代码可以参考https://blog.csdn.net/xushiyu1996818/article/details/90373591

Prim算法

	/** 通过prim算法，生成最小生成树

	 * 在算法的每一个阶段都可以通过选择边（u,v）,使得（u,v）的值是所有u在树上但v不在树上的边的值的最小者

	 * (这里设定边的方向是不在树上的v（为起始点）到树上的u，从而找到一个新的顶点并将它添加到这棵树中。

	 * 

	 * 如何计算连接树A结点和图G中树A以外的结点的所有边中选取权重最小的边

	 * 首先建立map，key为vertex，value为edge，

	 * 所有不在生成树中的节点，都是map的key，对应的value代表这个不在生成树的节点，到生成树中节点的最小的边。

	 * 一开始，value为edge的两端的都为自己，weight=maxDouble

	 * 每将一个结点j加入了树A，首先从map中去除这个节点

	 * 然后看map中剩余的节点到节点j的距离，如果这个边的距离小于之前边的距离，就将边替换成这个到节点j的边

	 * 最后下一个加入生成树的节点和边，就是map中value里的weight最小的边和对应的节点

	 * @param first  构成最小生成树的起点的标识
	 * @return  返回最小生成树构成的边
	 */
	public List generateMinTreePrim(T first){
		//存储最小生成树构成的边
		List result=new LinkedList<>();
		//首先建立map，key为vertex，value为edge
		HashMap, Edge> map=new HashMap<>();
		Iterator> vertexIterator=getVertexIterator();
		Vertex vertex;
		Edge edge;
		while(vertexIterator.hasNext()){
			//一开始，value为edge的两端的都为自己，weight=maxDouble
			vertex=vertexIterator.next();
			edge=new Edge(vertex, vertex, Double.MAX_VALUE);
			map.put(vertex, edge);
		}
		//first是构成最小生成树的起点的标识
		vertex=vertexMap.get(first);
		if(vertex==null){
			System.out.println("没有节点："+first);
			return result;
		}
		//所有不在生成树中的节点，都是map的key,如果map为空，代表所有节点都在树中
		while(!map.isEmpty()){
			//这次循环要加入生成树的节点为vertex，边为vertex对应的edge（也就是最小的边）
			edge=map.get(vertex);
			//每将一个结点j加入了树A，首先从map中去除这个节点
			map.remove(vertex);
			result.add(edge);
			System.out.println("生成树加入边，顶点："+vertex.getLabel()+
					" ，边的终点是："+edge.getEndVertex().getLabel()+" ，边的权值为： "+edge.getWeight());;
			//如果是第一个节点，对应的边是到自己的，删除
			if(vertex.getLabel().equals(first)){
				result.remove(edge);
			}
			//然后看map中剩余的节点到节点j的距离，如果这个边的距离小于之前边的距离，就将边替换成这个到节点j的边
			//在遍历替换中，同时发现距离最短的边minEdge
			Edge minEdge=new Edge(vertex, vertex, Double.MAX_VALUE);
			for(Vertex now:map.keySet()){
				edge=map.get(now);
				//newEdge为now到节点j的边
				Edge newEdge=now.hasNeighbourVertex(vertex);
				if(newEdge!=null&&newEdge.getWeight()

Kruskal算法

	/**通过kruskal算法，生成最小生成树

	 * 开始存在n颗单节点树，每次找到权值最短的一棵树将其合并起来

	 * 但是注意不要形成环。最后只剩下一棵树的时候，代表合并完成。
	 * 这里可以用map来记录每个端点在其所在连通图中的父端点

	 * map的key为每个顶点，value为每个顶点的父顶点，在一个连通分量中，总有一个端点的父端点是它自己（把它看成是一棵树的根节点）。

	 * 开始的时候初始化map为key和value都是vertex（因为每个端点所在的连通图只有自己）

	 * 每次要判断一条边(u, v)的两个端点是否在在不同的连通分量上，就找端点u和端点v在它们所在的连通图中的最底层的父端点

	 * 具体的方法是递归地找端点k的父端点，直至某个端点的父端点等于它自己

	 * 假设beginRoot=edge的beginVertex的根节点，endRoot=edge的endVertex的根节点，那么就要对它们进行判断

	 * 如果beginRoot==endRoot，说明结点beginVertex和结点endVertex在一个连通分量上，因此不能将其加入T

	 * 如果beginRoot!=endRoot，说明结点beginVertex和结点endVertex不在一个连通分量上，
	 * 这时可以将(beginVertex,endVertex)加入T，且令endRoot的父节点为beginRoot（beginRoot为两个子树的root）

	 *（注意：这里的beginRoot和endRoot是beginVertex和endVertex的根节点，最后是为根节点设置父节点，而不是为边的两端设置父节点）

	 * 
	 * @return
	 */
	public List generateMinTreeKruskal(){
		//存储最小生成树构成的边
		List result=new LinkedList<>();
		HashMap, Vertex> map=new HashMap<>();
		Iterator> vertexIterator=getVertexIterator();
		//用来存储所有的边的list
		ArrayList list=new ArrayList<>();
		Vertex vertex;
		Edge edge;
		while(vertexIterator.hasNext()){
			//一开始，父节点都是vertex自己，因为每个端点所在的连通图只有自己
			vertex=vertexIterator.next();
			map.put(vertex, vertex);
			//将这条顶点所有的边都加入list
			Iterator edgeIterator=vertex.getEdgeIterator();
			while(edgeIterator.hasNext()){
				edge=edgeIterator.next();
				list.add(edge);
			}
		}
		//对所有的边排序,从小到大
		Collections.sort(list, new Comparator() {
			@Override
			public int compare(Edge edge1,Edge edge2){
				return (int)(edge1.getWeight()-edge2.getWeight());
			}
			
		});
		for(Edge now:list){
			Vertex begin=now.getBeginVertex();
			Vertex end=now.getEndVertex();
			Vertex beginRoot=getRootVertex(map, begin);
			Vertex endRoot=getRootVertex(map, end);
			if(beginRoot.equals(endRoot)){
				//如果beginRoot==endRoot，说明结点beginVertex和结点endVertex在一个连通分量上，因此不能将其加入T
				continue;
			}
			else{
				//如果beginRoot!=endRoot，说明结点beginVertex和结点endVertex不在一个连通分量上，
				//这时可以将(beginVertex,endVertex)加入T，且令endRoot的父节点为beginRoot（beginRoot为两个子树的root）

				 result.add(now);
				 System.out.println("生成树加入边，顶点："+begin.getLabel()+
							" ，边的终点是："+end.getLabel()+" ，边的权值为： "+now.getWeight());;
				 map.put(endRoot, beginRoot);
			}			
		}				
		return result;		
	}
	
	/** 得到vertex的根节点
	 * @param map map的key为每个顶点，value为每个顶点的父顶点
	 * @param vertex 要查找的顶点
	 * @return
	 */
	public Vertex getRootVertex(HashMap, Vertex> map,Vertex vertex){
		while(true){
			Vertex parent=map.get(vertex);
			if(parent.equals(vertex)){
				//在一个连通分量中，总有一个端点的父端点是它自己（把它看成是一棵树的根节点）
				return vertex;
			}
			else{
				vertex=parent;
			}
		}
	}