xDeepFM论文解读(KDD2018)

xDeepFM: Combining Explicit and Implicit Feature Interactions for Recommender Systems

引言(ABSTRACT)
组合特征对与许多商业模型的成功都至关重要。受网络获取的原始数据的种类、容量和提取速度等限制，手工提取特征往往花费较大的代价。随着深度学习的兴起，最近研究者们提出了许多基于DNN的因子分解模型来学习高阶和低阶的交互特征。现在诸如DeepFM和Deep&Wide等模型都可以自动学习隐式的高维交互特征，并结合了低维特征，但是有一个缺点就是它们的高维特征都是在bite-wise的层面上进行交互的。本文提出了一种全新的压缩交互网络(Compressed Interaction Network(CIN))，能够在vector-wise级别学习显式的交互特征，CIN带有一些CNN和RNN的特点，作者进一步将CIN与经典的DNN融合成一个统一模型，命名为"eXtreme Deep Factorization Machine(xDeepFM)"。一方面，xDeepFM能够显式地学习一定的有界度特征交互;另一方面，它可以隐式地学习任意的低阶和高阶交互特性。

什么是bit-wise与vector-wise？
假设隐向量的维度为3维，如果两个特征(对应的向量分别为(a1,b1,c1) (a1,b1,c1)(a1,b1,c1)和(a2,b2,c2) (a2,b2,c2)(a2,b2,c2)）在进行交互时，交互的形式类似于f(w1∗a1∗a2,w2∗b1∗b2,w3∗c1∗c2) 的话，此时我们认为特征交互是发生在元素级（bit-wise）上。如果特征交互形式类似于f(w∗(a1∗a2,b1∗b2,c1∗c2))的话，那么我们认为特征交互是发生在特征向量级（vector-wise)。

1简介(INTRODUCTION)
1.1手动提取交互特征的缺点：

• 挖掘出高质量的交互特征需要非常专业的领域知识并且需要做大量的尝试，很耗时间；
• 在大型的推荐系统中，原生特征是海量的，手动挖掘交叉特征几乎不可能；
• 挖掘不出肉眼不可见的交叉特征。

1.2几种经典的特征提取模型：

• FM模型，用提取隐向量然后做内积的形式来提取交叉特征，扩展的FM模型可以提取随机的高维特征，但是主要的缺陷是：会学习所有的交叉特征，其中肯定会包含无用的交叉组合，另外一篇论文指出引入无用的交叉特征会引入噪音并降低模型的表现。
• DNN模型
  • FNN:“Factorisation-machine supported Neural Network (FNN)”，它在DNN之前使用了预训练的field embedding。
  • PNN:Product-based Neural Network (PNN),在embedding layer和DNN Input之间插入了一层product layer,不依赖于pre-trained FM。

1.3FNN和PNN的缺点都是忽略了低维交互特征，Wide&Deep和DeepFM模型通过混合架构解决了这种问题，但是它们同样存在缺点：a)它们学习到的高维特征是一种implicit fasion,没有一种公式可以明确推论出最终学习出来的交叉特征到底是多少维的;b)另一方面，其DNN部分是在bit-wise的层面下进行学习的，而经典的FM架构是在vetor-wise层面学习的。

2.PRELIMINARIES
2.1 Embedding Layer
在计算机视觉或者自然语言处理领域，输入往往是图片或者文字文本，这些都是空间或者时间上相关的，因此可以用DNN直接作用于结构紧制的原始特征上。但是在推荐系统中，输入的原始特征稀疏，维数大，没有明显的时空相关性。在原始特征输入上应用嵌入层，将其压缩为低维、密集的实值向量。


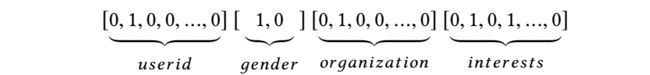
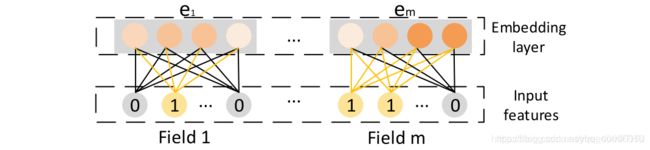
虽然输入的每个feature的长度可能不同，但是经过embedding layer后，长度均为D,保持一致。

2.2隐式的高阶交互
FNN，Deep Crossing以及Wide＆Deep的深层部分利用 field embedding $e$上的前馈神经网络来学习高阶特征交互，具体的前向传播过程如下：

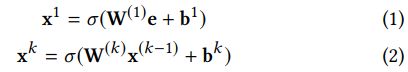
PNN和DeepFM除了在嵌入向量e上应用DNN之外，还在架构中引入了双向交互层。 因此，bit-wise和vector-wise相互作用都包含在他们的模型中。 PNN和DeepFM之间的主要区别在于：PNN将product layer的输出连接到DNN，而DeepFM将FM层直接连接到输出单元。PNN 与 DeepFM 结构如下图所示，属于元素级（bit-wise）的特征交互，也可以理解为相同 field 中的 embedding vector 内的元素也会相互影响。

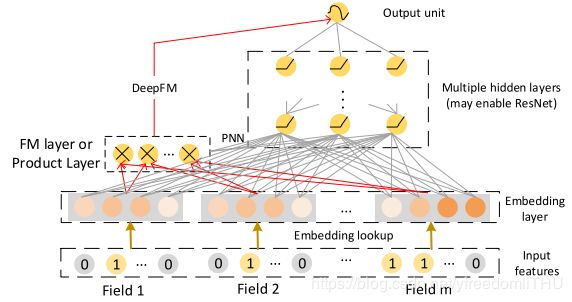
2.3显式的高阶交互
Cross Network(CrossNet)的结构图如下所示：

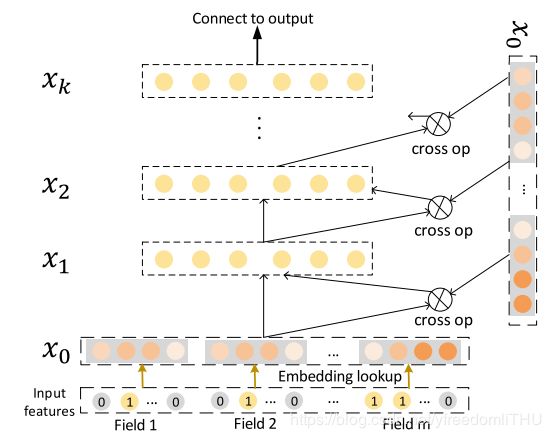
Cross-Network的目标在于明确地模拟高阶特征交互。 与传统的完全连接的前馈网络不同，隐藏层通过以下交叉操作计算：

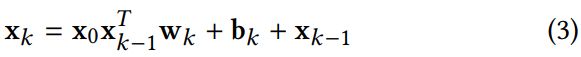
其中$w_k,b_k,x_k$分别是第k层的权重，偏置和输出，论文作者认为CrossNet学习了一种特殊类型的高阶特征交互，其中CrossNet中的每个隐藏层都是x0的标量倍数。并给出了证明：

这个模型有以下两个缺点：（1）CrossNet的输出以特殊形式限制，每个隐藏层是$x_0$标量的倍数; （2）互动以 bit-wise 方式进行。

3.OUR PROPOSED MODEL
3.1 Compressed Interaction Network(CIN)
鉴于上述方法存在的不足，作者提出的CIN模型主要具备以下特点：（1）相互作用在 vector-wise层面，而不是在 bit-wise水平上应用; （2）显式度量高阶特征相互作用; （3）网络的复杂性不会随着交互程度呈指数级增长。

每一层具体的计算公式如下：

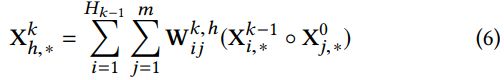
如图中所示，第k层有$H_k$个特征向量，计算主要分三个过程进行:
(1)如(a)中所示，这主要是点乘的过程，根据原始的特征矩阵$x_0$和前一层的输出$x^k$,得到中间接结果$z^{k+1}$（三维张量）；(2)图(b)是featuremap的过程，对于生成的中间结果$z^{k+1}$,类似于卷积神经网络的计算方法，对于第k层的中间变量$z^{k+1}$,利用$H_{k+1}$个尺寸大小为$m\ast H_k$的卷积核得到下一层的隐层状态。但是具体的卷积计算细节与CNN有所不同，CIN中一个神经元相关的接受域是垂直于特征维度D的整个平面，而CNN中的接受域是当前神经元周围的局部小范围区域，因此CIN中经过卷积操作得到的特征图是一个向量，而不是一个矩阵。

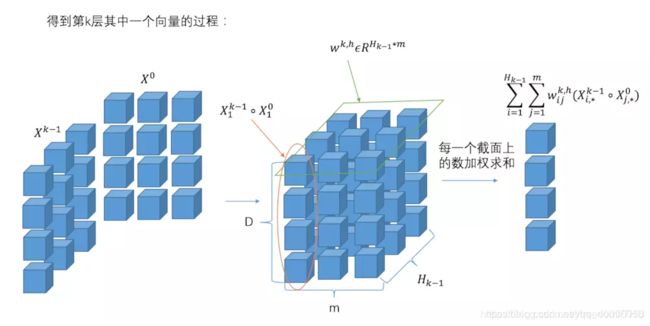
(3)如图©所示，对于每一层的隐状态$x^{k+1}$,将每个(第k层有$H_k$个)特征向量求和(即图中sum pooling过程),最后将每一层的结果拼接起来，作为最后的输出。CIN实现了输出单元可以得到不同阶数的特征交互模式。此外CIN的计算过程与机构与RNN十分类似，，对于每一层的隐状态都是根据前一层的隐状态和额外的输入数据计算得到的。

4.xDeepFM
将CIN和DNN结合起来，得到xDeepFM,组合模型与Wide&Deep, DeepFM十分类似，结构如下图所示：

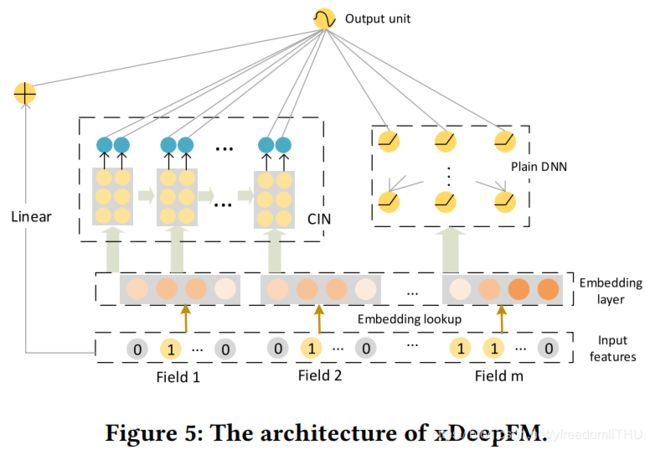
一方面包括低阶和高阶特征交互;另一方面，它既包括隐式的功能交互，也包括显式的功能交互。
输出结果如下：

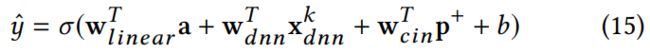
其中，$x_{dnn}^k,p^{+}$分别是DNN和CIN的输出。
损失函数：

论文代码：https://github.com/Leavingseason/xDeepFM