多智能体强化学习博弈系列（2）- 模糊Q-Learning

关于模糊系统见上一篇。

游戏描述：

以多人领土保卫游戏（guarding territory）为例：进攻者采取最佳策略（提前计算出的纳什均衡点），防卫者通过强化学习，不断优化截击位置。目标是成功截击进攻者，且截击位置距离领土范围最远。

这一章节采用的RL算法是Q-learning。防卫者作为智能体，输入和输出分别经过模糊化和去模糊化处理。

模糊系统

$n$个输入变量的连续输入空间被离散化为$M$个模糊规则，输出变量为单一值，取值空间为连续范围。 规则$l(l=1,\cdots ,M)$可以表示为：

$$R^l:\text{IF }{x}_1\text{ is }{F}_1^l,\cdots ,\text{ and }{x}_n\text{ is }{F}_n^l\text{ THEN }u=c^l$$

其中$x=(x_1,\cdots ,x_n)$是输入变量，$F_i^l$是对应各个输入变量和模糊规则的模糊集合，$u^l$是每个规则的推理输出，$c^l$是每个集合的中心点（离散的行为）。

使用_product inference engine_, singleton membership function，加权平均去模糊化，最终的系统输出可以表示为：

$$U(x)=\frac{{\sum }_{l=1}^M(\left({\Pi }_{i=1}^n{\mu }^{F_i^l}(x_i)\right)\cdot c^l)}{{\sum }_{l=1}^M\left({\Pi }_{i=1}^n{\mu }^{F_i^l}(x_i)\right)}=\sum _{l=1}^M{\Phi }^l{c}^l$$

其中${\mu }^{F_i^l}$是模糊集合$F_i^l$的membership function。

对应的java代码实现(实现使用了triangular membership function，代码实现了${\Phi }_l$的计算):

/**
 * @param a: lower limit
 * @param b: upper limit
 * @param x: input value
 * @return value of membership function F(x)
 */
private double calculateTriangularMF(double a, double b, double x) {
	double m = (a+b)/2;
	if (x <= a) {
		return 0;
	} else if (x <= m) {
		return (x-a)/(m-a);
	} else if (x <= b) {
		return (b-x)/(b-m);
	}else {
		return 0;
	}
}

/**
 * @param x: input vector. same length as inputBucket.
 * @param l: index of the rule in question
 * @return membership degrees \Phi_l (altogether M=n1*n2...*ni rules, l \in M)
 */
private double calculatePhi_l_numerator(int l, double[] x) {
	List<Integer> combi = inputCombination.get(l);
	ValContainer<Double> numerator = new ValContainer<Double>(1.0);
	for (int i=0; i<combi.size(); i++) {
		double step = (inputUpper[i] - inputLower[i]) / inputBucket[i];
		int bucket = combi.get(i);
		double a = inputLower[i] + (bucket - 1) * step;
		double b = inputLower[i] + (bucket + 1) * step;
		double mf = calculateTriangularMF(a, b, x[i]);
		numerator.setVal(numerator.getVal() * mf);
	}
	return numerator.getVal();
}

/**
 * @param x: input vector.
 * @return \Phi value for all M rules.
 */
private void calculatePhi_l(double[] x) {
	double[] numerators = new double[M];
	ValContainer<Double> denominator = new ValContainer<Double>(0.0);
	for (int l=0; l<M; l++){
		numerators[l] = calculatePhi_l_numerator(l, x);
		denominator.setVal(denominator.getVal() + numerators[l]);
	}
	if (denominator.getVal()!=0){
		phi_l = DoubleStream.of(numerators).map(d->d/denominator.getVal()).toArray();
	}
}

Q-learning

将智能体的连续行为空间离散化为m种行为，集合为$A=\{a_1,a_2,\cdots ,a_m\}$。这些离散化行为作为每个规则对应每种输入变量的推理结果，在上一小节中实际是$c^l$。所以用$a^l$替换公式中的$c^l$得到最终推理的行为输出：

$$U_t(x_t)=\sum _{l-1}^M{\Phi }_t^l{a}_t^l$$

其中行为用$ϵ$-greedy方法选择，保证随机性：

$$a^l=\{\begin{array}{ll}\text{random action from A}& Prob(ϵ)\\ argma{x}_{a\in A}(q(l,a))& Prob(1-ϵ)\end{array}$$

$q(l,a)$是对应的行为价值。

同样的可以得到行为的全局价值：

$$Q_t(x_t)=\sum _{l-1}^M{\Phi }_t^l{q}_t(l,a_t^l)$$

以及预测的全局最大价值：

$$Q_t^{\ast }(x_t)=\sum _{l-1}^M{\Phi }_t^{l}ma{x}_{a\in A}{q}_t(l,a)$$

由此可以计算TD-error为：

$${\widetilde{ϵ}}_{t+1}=r_{t+1}+\gamma Q_t^{\ast }(x_{t+1})-Q_t(x_t)$$

根据TD-error，带入Q-learning公式，得到更新的行动价值：

$$q_{t+1}(l,a_t^l)=q_t(l,a_t^l)+\eta {\widetilde{ϵ}}_{t+1}{\Phi }_t^l$$

算法描述：

Initialize $q(\cdot )=0$ and $Q(\cdot )=0$
for Each time step do:
    Choose action for each rule based on $ϵ$ at time t;
    Compute global continuous action $U_t(x_t)$;
    Compute $Q_t(x_t)$;
    Take $U_t(x_t)$ and run the game;
    Obtain reward $r_{t+1}$ and new inputs $x_{t+1}$;
    Compute $Q_t^{\ast }(x_{t+1})$;
    Compute TD error ${\widetilde{ϵ}}_{t+1}$;
    Update $q_{t+1}(l,a_t^l),l=1,\cdots ,M$;
end for

对应的java代码实现

/**
 * Choose action for each rule.
 * @param star: if true then update best action index. if false then update chosen action index.
 */
private void chooseAction(boolean star, int dots) {
	Random rand = new Random();
	for (int l=0; l<M; l++) {
    	double r = rand.nextDouble();
		List<Double> prob = Arrays.stream(q_la[l]).boxed().collect(Collectors.toList());
		List<Integer> allMaxes = IntStream.range(0, prob.size()).boxed()
						                .filter(i -> prob.get(i).equals(Collections.max(prob)))
						                .collect(Collectors.toList());
		if (star) {
			if (dots>BURNIN) {
				bestActions[l] = allMaxes.get(rand.nextInt(allMaxes.size()));
			} else {
				bestActions[l] = rand.nextInt(actions.length);
			}
				
		} else {
        	if (r<=epsilon) {
        		int idx = rand.nextInt(actions.length);
        		chosenActions[l] = idx;
        	} else {
    			chosenActions[l] = allMaxes.get(rand.nextInt(allMaxes.size()));
        	}
		}
	}
}

/**
 * get inferred action.
 */
private void calculateU() {
	U = 0.0;
	for (int l=0; l<M; l++) {
		U = U + phi_l[l] * actions[chosenActions[l]];
	}
}

/**
 * get global Q value.
 * @param star: if true then calculate and update Q*. if false then calculate and update Q.
 */
private void calculateQ(boolean star) {
	if (star) {
		Qstar = 0.0;
		for (int l=0; l<M; l++)
			Qstar = Qstar + phi_l[l] * q_la[l][bestActions[l]];
	} else {
		Q = 0.0;
		for (int l=0; l<M; l++){
			Q = Q + phi_l[l] * q_la[l][chosenActions[l]];
        	}
	}
}

/**
 * calculate temporal difference error.
 */
private double calculateTDerror() {
	double reward = calculateRewardShaping();
	return reward + gamma * Qstar - Q;
}

/**
 * update q(l,a)
 */
private void updateQla() {
	double TDerror = calculateTDerror();
	for (int l=0; l<M; l++) {
		q_la[l][chosenActions[l]] = q_la[l][chosenActions[l]] + eta * TDerror * phi_l[l];
		q_la[l][chosenActions[l]] = q_la[l][chosenActions[l]] < 0 ? 0 : q_la[l][chosenActions[l]];
	}
	// normalize
	for (int l=0; l<M; l++) {
		double tmp = Arrays.stream(q_la[l]).sum();
		if (tmp==0) {
			Arrays.fill(q_la[l], 1.0/q_la[l].length);
		} else {
			q_la[l] = Arrays.stream(q_la[l]).map(x->x/tmp).toArray();
		}
	}
}

另外由于这种策略游戏的全局reward要等到每局结束后才能获得，所以在实际模拟中采用了reward shaping的方法，根据中间的过渡reward，预测最终reward。实时证明：一个好的中间reward对于智能体的性能有非常大的影响。如果以后数据科学中的特征工程和建模多少会被autoML所取代，至少对于这类目标函数的设计仍然需要人工解决。

对应的代码实现

private double calculateRewardShaping() {

	// difference between invader angle and territory border angle (with regard to the defender).
	double angle = - Math.abs(Math.PI - Math.abs(inputX[0]-inputX[1])) / Math.PI;
	double angleReward = angle - previousAngle; 
	
	// distance between invader and defender.
	double distReward;
	if (Math.signum(angleReward) >= 0) {
		distReward = previousDistToInvader / (distToInvader);
	} else {
		distReward = distToInvader / (previousDistToInvader);
	}
	previousAngle = angle;
	previousDistToInvader = distToInvader;
	
	if (distToInvader < bestDistToInvader) {
		bestDistToInvader = distToInvader;
		bestDist_q_la = q_la.clone();
	}
	
	return angleReward * distReward;
}

模拟结果

随机设置进攻者和防卫者的起始位置，固定领土的范围。进攻者在游戏开始前会根据防卫者位置计算最佳策略（NE strategy)，而防卫者只有地图信息，策略是随机初始化的。所有玩家的移动速度相同，可以随时转向任何方向。

设置游戏自动进行n=100次，在此期间防卫者不断学习当进攻者和领土处于不同相对位置时的行进方向。在每轮游戏中使用reward shaping，如果最终赢得游戏，会保留q-table（i.e.对应不同模糊规则的行为概率）；如果输掉游戏，则以一定加权更新q-table。

两个进攻者，三个防卫者的模拟结果：

round 9 won: 3 out of the last 10 games
round 19 won: 14 out of the last 10 games
round 29 won: 15 out of the last 10 games
round 39 won: 10 out of the last 10 games
round 49 won: 9 out of the last 10 games
round 59 won: 17 out of the last 10 games
round 69 won: 13 out of the last 10 games
round 79 won: 12 out of the last 10 games
round 89 won: 14 out of the last 10 games
round 99 won: 19 out of the last 10 games

第1轮：红色为防卫者，绿色为进攻者，灰色为领土范围。进攻者的目标是到达领土，防卫者的目标是在进攻者到达前截击。在游戏中除了用圆点标识每一步各个player的位置，也用实线标识了之前的行进路径。进攻者的行进路线是在初始化后就确定的（进攻者的转向方向和目标位置都由黄色圆点标识）；防卫者没有规定行进路线，游戏开始时是通过随机初始化：

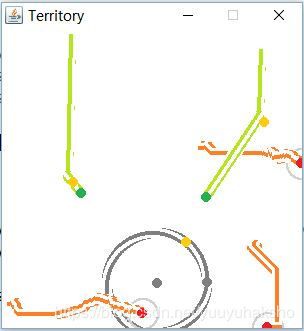
第3轮：有相似输入，并已经赢得过游戏的防卫者智能体，已经可以实施截击：

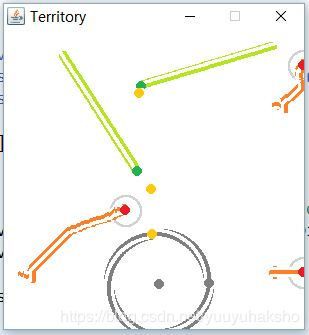
第60轮：多个防守智能体的截击位置都有提高：

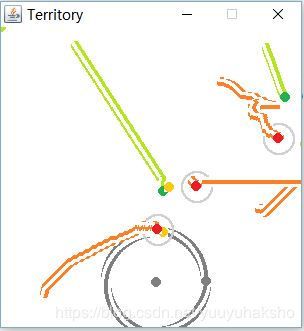
下一篇会介绍其他RL算法的实现。