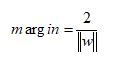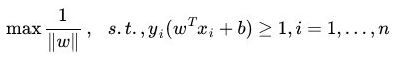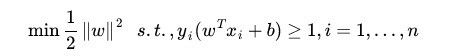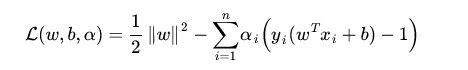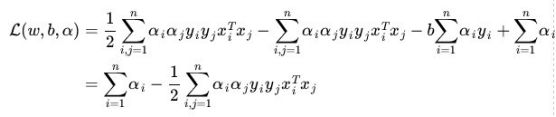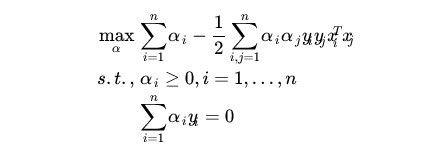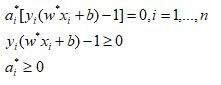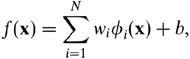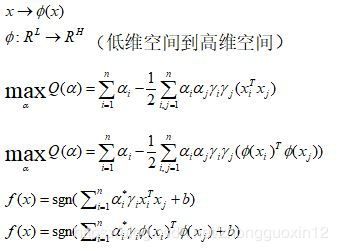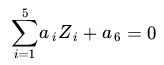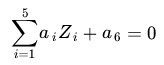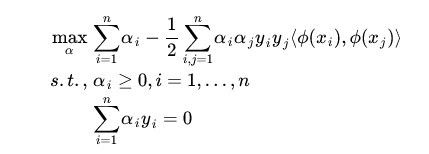人工智能(二):SVM
一、一些概念的初步了解
1、超平面
根据百度百科的解释,超平面是n维欧式空间中余维度等于一的线性子空间,也就是必须是(n-1)维度。这是平面中的直线、空间中的平面之推广(n大于3才被称为“超平面”),是纯粹的数学概念,不是现实的物理概念。因为是子空间,所以超平面一定经过原点。
n 维空间中的超平面是由方程:![]()
定义的子集,其中![]() 是不全为零的常数。
是不全为零的常数。
超平面是为了分割分类用的,超平面将空间划分为三部分,超平面本身,超平面上部,超平面下部。举例,对于二维空间来说,超平面为一维直线,这里定义超平面本身方程为wx+b=0,则超平面上部wx+b>0,超平面下部wx+b<0。代入x的值,计算得到的wx+b,根据与0的关系,即可知道当前的x属于哪一类。超平面参数其实是不唯一的,超平面的参数可以增大或者缩小任意正的尺度而不影响分类结果,实际上有无数个解。
2、最优超平面
假定训练数据![]() 可以被一个超平面分开,如果这个向量集合被超平面没有错误地分开,并且离超平面最近的向量与超平面之间的距离(称作间隔margin)是最大的,则我们说这个向量集合被这个最优超平面(或最大间隔超平面)分开。
可以被一个超平面分开,如果这个向量集合被超平面没有错误地分开,并且离超平面最近的向量与超平面之间的距离(称作间隔margin)是最大的,则我们说这个向量集合被这个最优超平面(或最大间隔超平面)分开。
二、最优分类面
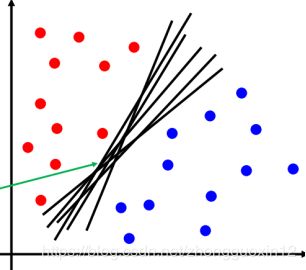
如下图所示,现在有一个二维平面,平面上有两种不同的数据,分别用绿点和红点表示。由于这些数据是线性可分的,所以可以用一条直线将这两类数据分开,这条直线就相当于一个超平面,超平面一边的数据点所对应的y全是-1 ,另一边所对应的y全是1。
这个超平面可以用分类函数表示,当f(x) 等于0的时候,x便是位于超平面上的点,而f(x)大于0的点对应 y=1 的数据点,f(x)小于0的点对应y=-1的点,如下图所示:
接下来的问题是,如何确定最优超平面呢?从直观上而言,这个超平面应该是最适合分开两类数据的直线。而判定“最适合”的标准就是这条直线离直线两边的数据的间隔最大。所以,得寻找有着最大间隔的超平面。对一个数据点进行分类,当超平面离数据点的“间隔”越大,分类的确信度(confidence)也越大。所以,为了使得分类的确信度尽量高,需要让所选择的超平面能够最大化这个“间隔”值。
不妨把离分类面最近的样本的决策函数值归一化为1,即强制:
即
所谓最优分类面,就是在线性可分情况下,要求分类线不但能将两类无错误地分开,而且要使两类的分类空隙最大,即: 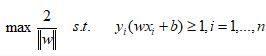 ,其中,s.t.,即subject to的意思,它导出的是约束条件。
,其中,s.t.,即subject to的意思,它导出的是约束条件。
三、支持向量与支持向量机
回顾下几何间隔的定义,可知:如果令函数间隔等于1(之所以令等于1,是为了方便推导和优化,且这样做对目标函数的优化没有影响),则有 = 1 / ||w||且,从而上述目标函数转化成了
相当于在相应的约束条件下,最大化这个1/||w||值,而1/||w||便是几何间隔。
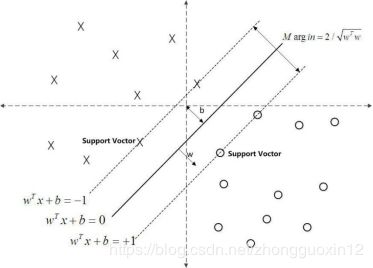
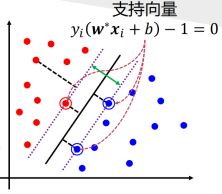
如下图所示,中间的实线便是寻找到的最优超平面(Optimal Hyper Plane),其到两条虚线边界的距离相等,这个距离便是几何间隔,两条虚线间隔边界之间的距离等于2,而虚线间隔边界上的点则是支持向量。由于这些支持向量刚好在虚线间隔边界上,所以它们满足![]() (这与我们前面说的强制化刚好吻合)。
(这与我们前面说的强制化刚好吻合)。
具体如何求解,我这里就不做过多解释了,具体可以查看:《支持向量机通俗导论(理解SVM的三层境界)》,是一篇博客,感觉已经是中文介绍SVM里面最好的了。
我这里为了说明理论代表的事实,简要介绍一些关键步骤,由于求![]() 的最大值相当于求
的最大值相当于求![]() 的最小值,所以上述目标函数等价于(w由分母变成分子,从而也有原来的max问题变为min问题,很明显,两者问题等价):
的最小值,所以上述目标函数等价于(w由分母变成分子,从而也有原来的max问题变为min问题,很明显,两者问题等价):
通过拉格朗日对偶性(Lagrange Duality)变换到对偶变量 (dual variable) 的优化问题,即通过求解与原问题等价的对偶问题(dual problem)得到原始问题的最优解,这就是线性可分条件下支持向量机的对偶算法,这样做的优点在于:一者对偶问题往往更容易求解;二者可以自然的引入核函数,进而推广到非线性分类问题。
拉格朗日对偶性,简单来讲,通过给每一个约束条件加上一个拉格朗日乘子(Lagrange multiplier),定义拉格朗日函数(通过拉格朗日函数将约束条件融合到目标函数里去,从而只用一个函数表达式便能清楚的表达出我们的问题):
![]() 为拉格朗日乘子
为拉格朗日乘子
分别对w和b求偏微分并令它们等于0,可得对偶问题。
求![]() 对的极大,即是关于对偶问题的最优化问题。经过上面第一个步骤的求w和b,得到的拉格朗日函数式子已经没有了变量w,b,只有
对的极大,即是关于对偶问题的最优化问题。经过上面第一个步骤的求w和b,得到的拉格朗日函数式子已经没有了变量w,b,只有![]() 。从上面的式子得到:
。从上面的式子得到:
(在这里还有一个需要思考的地方,即为什么要转化为对偶问题,前面说了两个优点,但是真的只有那两个吗,其实在数学层面还有一个,需要大家去思考,在这里我先提一下,有答案的可以评论)
对于一个数据点 x 进行分类,实际上是通过把 x 带入到算出结果然后根据其正负号来进行类别划分的。而前面的推导中我们得到:
![]()
即最优超平面的权值向量等于训练样本以一定的系数加权后的线性组合。可以得到分类函数为:
这里的形式的有趣之处在于,对于新点x的预测,只需要计算它与训练数据点的内积即可(表示向量内积),这一点至关重要,是之后使用 内核函数进行非线性推广的基本前提。此外,所谓 Supporting Vector 也在这里显示出来——事实上,所有非Supporting Vector 所对应的系数都是等于零的,因此对于新点的内积计算实际上只要针对少量的“支持向量”而不是所有的训练数据即可。大概说一下原因:
前面的公式根据KT条件,拉格朗日函数:
对应的鞍点(即最优解)满足:
可以推出![]() 时,必定有
时,必定有![]() ,必定有
,必定有![]() ,它们对应的样本就是支持向量(Support Vectors or SVs)。该结论说明了支持向量决定了最优超平面,这种分类器被称为支持向量机(Support Vectors Machine),即SVM,说明远处的样本不影响分类面。
,它们对应的样本就是支持向量(Support Vectors or SVs)。该结论说明了支持向量决定了最优超平面,这种分类器被称为支持向量机(Support Vectors Machine),即SVM,说明远处的样本不影响分类面。
上面所讲的都是在线性情况下,如果是非线性呢?
事实上,大部分时候数据并不是线性可分的,这个时候满足这样条件的超平面就根本不存在。在上文中,我们已经了解到了SVM处理线性可分的情况,那对于非线性的数据SVM咋处理呢?对于非线性的情况,SVM 的处理方法是选择一个核函数K ,通过将数据映射到高维空间,来解决在原始空间中线性不可分的问题。
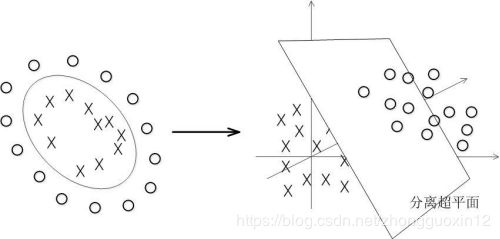
具体来说,在线性不可分的情况下,支持向量机首先在低维空间中完成计算,然后通过核函数将输入空间映射到高维特征空间,最终在高维特征空间中构造出最优分离超平面,从而把平面上本身不好分的非线性数据分开。如图所示,一堆数据在二维空间无法划分,从而映射到三维空间里划分:
而在我们遇到核函数之前,如果用原始的方法,那么在用线性学习器学习一个非线性关系,需要选择一个非线性特征集,并且将数据写成新的表达形式,这等价于应用一个固定的非线性映射,将数据映射到特征空间,在特征空间中使用线性学习器,因此,考虑的假设集是这种类型的函数:
这里:![]() 是从输入空间到某个特征空间的映射,这意味着建立非线性学习器分为两步:
是从输入空间到某个特征空间的映射,这意味着建立非线性学习器分为两步:
1、首先使用一个非线性映射将数据变换到一个特征空间F
2、然后在特征空间使用线性学习器分类
而由于对偶形式就是线性学习器的一个重要性质,这意味着假设可以表达为训练点的线性组合,因此决策规则可以用测试点和训练点的内积来表示:
一开始的函数表明![]() 只是一个点,变换为映射以后,只要找到
只是一个点,变换为映射以后,只要找到![]() 的结果,就可以实现非线性的分类,如果有一种方式可以在特征空间中直接计算内积
的结果,就可以实现非线性的分类,如果有一种方式可以在特征空间中直接计算内积![]() ,就像在原始输入点的函数中一样,就有可能将两个步骤融合到一起建立一个非线性的学习器,这样直接计算法的方法称为核函数方法:
,就像在原始输入点的函数中一样,就有可能将两个步骤融合到一起建立一个非线性的学习器,这样直接计算法的方法称为核函数方法:
这样我们可以在实际情况中直接使用K,而不用精确需要知道![]() ,因为从低维到高维的选择太多。而且高维空间很难理解。来看个核函数的例子。如下图所示的两类数据,分别分布为两个圆圈的形状,这样的数据本身就是线性不可分的,此时咱们该如何把这两类数据分开呢(下文将会有一个相应的三维空间图)?
,因为从低维到高维的选择太多。而且高维空间很难理解。来看个核函数的例子。如下图所示的两类数据,分别分布为两个圆圈的形状,这样的数据本身就是线性不可分的,此时咱们该如何把这两类数据分开呢(下文将会有一个相应的三维空间图)?
事实上,上图所述的这个数据集,是用两个半径不同的圆圈加上了少量的噪音生成得到的,所以,一个理想的分界应该是一个“圆圈”而不是一条线(超平面)。如果用和来表示这个二维平面的两个坐标的话,我们知道一条二次曲线(圆圈是二次曲线的一种特殊情况)的方程可以写作这样的形式:
注意上面的形式,如果我们构造另外一个五维的空间,其中五个坐标的值分别为![]() 那么显然,上面的方程在新的坐标系下可以写作:
那么显然,上面的方程在新的坐标系下可以写作:
关于新的坐标,这正是一个 hyper plane 的方程!也就是说,如果我们做一个映射,将按照上面的规则映射为,那么在新的空间中原来的数据将变成线性可分的,从而使用之前我们推导的线性分类算法就可以进行处理了。这正是 Kernel 方法处理非线性问题的基本思想。再进一步描述 Kernel 的细节之前,不妨再来看看上述例子在映射过后的直观形态。当然,你我可能无法把 5 维空间画出来,不过由于我这里生成数据的时候用了特殊的情形,所以这里的超平面实际的方程是这个样子的(圆心在轴上的一个正圆):
因此我只需要把它映射到这样一个三维空间中即可,下图即是映射之后的结果,将坐标轴经过适当的旋转,就可以很明显地看出,数据是可以通过一个平面来分开的:
映射成:![]()
而其中的可以通过求解如下 dual 问题而得到的:
这样一来问题就解决了吗?似乎是的:拿到非线性数据,就找一个映射,然后一股脑把原来的数据映射到新空间中,再做线性 SVM 即可。不过事实上好像并没有这么简单。在前民我们是利用![]() ,这样一个变换,把低维空间映射到高维空间,我们对一个二维空间做映射,选择的新空间是原始空间的所有一阶和二阶的组合,得到了五个维度;如果原始空间是三维(一阶、二阶和三阶的组合),那么我们会得到:3(一次)+3(二次交叉)+3(平方)+3(立方)+1(x1*x2*x3)+2*3= 19维的新空间,这个数目是呈指数级爆炸性增长的,从而势必给计算带来非常大的困难,而且如果遇到无穷维的情况,就根本无从计算了。
,这样一个变换,把低维空间映射到高维空间,我们对一个二维空间做映射,选择的新空间是原始空间的所有一阶和二阶的组合,得到了五个维度;如果原始空间是三维(一阶、二阶和三阶的组合),那么我们会得到:3(一次)+3(二次交叉)+3(平方)+3(立方)+1(x1*x2*x3)+2*3= 19维的新空间,这个数目是呈指数级爆炸性增长的,从而势必给计算带来非常大的困难,而且如果遇到无穷维的情况,就根本无从计算了。
此时我们才引入核函数,即可以实现从低维到高维的映射,又不导致最后结果的指数级增长。
举个例子:
当然还可以选择多种不同的映射。我们发现其实不需要映射到高维空间,再根据内积的公式进行计算,而可以字节在低维空间中进行计算,而不需要写出映射后的结果,即可以省去求映射函数的过程。 我们把这里的计算两个向量在隐式映射过后的空间中的内积的函数叫做核函数 (Kernel Function) ,例如,在刚才的例子中,我们的核函数为:![]() ,核函数可以简化映射空间中的内积运算,正好我们SVM的分类函数中需要计算的样本都是以内积的形式出现的,所以利用核函数可以解决我们的非线性分类问题,还可以避免繁琐的计算。
,核函数可以简化映射空间中的内积运算,正好我们SVM的分类函数中需要计算的样本都是以内积的形式出现的,所以利用核函数可以解决我们的非线性分类问题,还可以避免繁琐的计算。
常见的核函数如下:
但是我们并不是任何时候都可以使用核函数的,必须满足一定的条件才行,这里引出一个定理:
核函数的本质其实是对样本进行包装,使样本在某个高维空间中可分,而却不知道高维空间是什么。
三、SVM案例
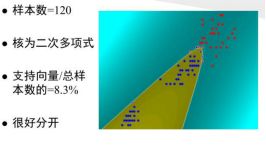
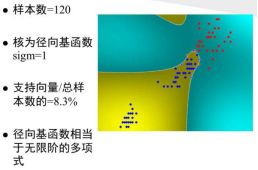
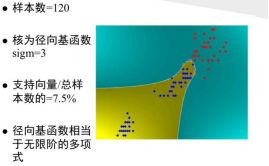
SVM的思想是要求分类线不但能将两类无错误地分开,并且要使两类的分类空隙最大,由于在很多实际分类问题中,由于高推广能力,SVM表现的都很好,比如文本分类,基因数据分类。
核函数的选择对结果有很大的影响,但是核函数如何选择并没有统一的方法,需要靠自己的工程实践经验。
提个小问题,如何把三个类别分开?
参考文献:
https://blog.csdn.net/v_JULY_v/article/details/7624837