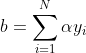《统计学习方法》——感知机与支持向量机
机器学习有三要素:模型,策略,方法。模型是所有函数的假设空间,策略是模型选择标准,方法是选择最优模型的算法。其中模型是输入变量的线性函数,策略用损失函数、风险函数度量。损失函数度量一次预测好坏,(0-1损失函数,平方损失函数,绝对损失函数,对数损失函数),风险函数度量平均预测好坏(经验风险,结构风险)。求支持向量机的最优解,可以理解为求损失函数极小化问题的最优解。
基本原理:现在有一些数据点,用一条直线对这些数据进行划分,将它们分为两类,叫做线性拟合,这条直线叫做分隔超平面。
为什么把直线叫平面?假设这些数据点散布在一个三位空间,那么这条直线变成一个平面。假设数据集是N维,那么这条直线变成N-1维的平面,也就是真正的超平面。假设输入空间(特征空间)x={x1,x2,...xn},输出空间y={+1,-1}表示实例的类别。输入到输出的映射为:f(x)=sign(wx+b). 称为感知机。w是特征的权值,b是偏置。sign是符号函数。
定义损失函数:
![]()
其中的xi与yi都是误分类的点的集合。例如,wx+b>0时y=-1,这个点就是误分类点。通过加负号使得损失函数永远为正。
问题转化为求一个损失函数使得误分类点最小,即求:![]() ,采用随机梯度下降法。定义梯度为:
,采用随机梯度下降法。定义梯度为:
(1)设初始超平面![]()
(2)随机选取一个误分类点,对w,b进行更新:
![]() ,
, ![]() ,
,
![]() 是步长,或者学习率。
是步长,或者学习率。
重复(2)直到损失函数减小到一定范围内。
以上是感知机学习算法的原始形式。下面说感知机学习算法的对偶形式:
在原始形式的基础上,逐步修改w,b。设对同一误分类点![]() 修改了n次,则最后w,b关于
修改了n次,则最后w,b关于![]() 的增量分别是
的增量分别是![]() 和
和![]() ,
, ![]() 。综合所有误分类点,最后求得的w,b可表示为:
。综合所有误分类点,最后求得的w,b可表示为:
那么感知机算法对偶形式就是: 输入数据集和步长,输出w和b。
(1)设![]()
(2)取样本点![]() ,如果是误分类点,即
,如果是误分类点,即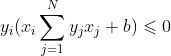 , 那么更新样本点对应的
, 那么更新样本点对应的![]() 和总偏置d
和总偏置d
![]()
![]()
重复(2)至误差降低至一定范围内。
为了方便,事先将样本点内积![]() 计算出来存入矩阵,这个矩阵就是Gram矩阵。
计算出来存入矩阵,这个矩阵就是Gram矩阵。
---------------------------------------------------------------------------------
感知机是支持向量机的基础,由感知机误分类最小策略可以得到分离超平面(无穷多个),支持向量机利用间隔最大化求得最优分离超平面(1个)。间隔最大化就是在分类正确的前提下提高确信度。比如,A离超平面远,若预测点就是正类,就比较确信是正确的。点C离超平面近,就不那么确信正确。
定义超平面关于![]() 样本点的函数间隔:
样本点的函数间隔:![]()
而超平面关于样本数据集T的函数间隔为:![]() .
.
如果对超平面法向量给予约束,如||w||=1,这时函数间隔变为了几何间隔。几何间隔和函数间隔的关系是 ![]() 。
。
这时候其实求的最大值是几何间隔,只不过w不受![]() 的约束。为了最后获得w,b的一组确定值而不是倍数值,我们对
的约束。为了最后获得w,b的一组确定值而不是倍数值,我们对![]() 做一些限制,以保证解唯一的。为了简便取
做一些限制,以保证解唯一的。为了简便取![]() 。这样的意义是将全局的函数间隔定义为1,也即是将离超平面最近的点的距离定义为
。这样的意义是将全局的函数间隔定义为1,也即是将离超平面最近的点的距离定义为![]() 。由于求
。由于求![]() 的最大值相当于求
的最大值相当于求![]() 的最小值,因此改写后结果为:
的最小值,因此改写后结果为:
![]()
由前面感知机得到的公式可知,最后学习得到的w公式为:
w分量的内积最小化后,即可得出所求w和b向量。
---------------------------------------------------------------------------------
核函数
线性支持向量机解决线性分类问题。对于非线性分类问题,可以采用非线性支持向量机解决。具体为:
采取一个非线性变换,将非线性问题转变为线性问题。再通过线性支持向量机解决,这就是核技巧。
设T是输入空间(欧式空间或离散集合),H为特征空间(希尔伯特空间)。如果存在一个映射
![]()
使得对于所有的![]()
![]()
在学习与预测中只定义核函数,而不显式地定义映射函数![]() .
.
希尔伯特空间是欧几里德空间的一个推广,其不再局限于有限维的情形。