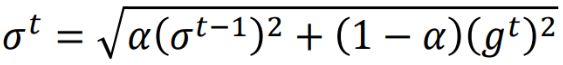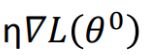【李宏毅机器学习笔记】8、Tips for Training DNN
【李宏毅机器学习笔记】1、回归问题(Regression)
【李宏毅机器学习笔记】2、error产生自哪里?
【李宏毅机器学习笔记】3、gradient descent
【李宏毅机器学习笔记】4、Classification
【李宏毅机器学习笔记】5、Logistic Regression
【李宏毅机器学习笔记】6、简短介绍Deep Learning
【李宏毅机器学习笔记】7、反向传播(Backpropagation)
【李宏毅机器学习笔记】8、Tips for Training DNN
【李宏毅机器学习笔记】9、Convolutional Neural Network(CNN)
【李宏毅机器学习笔记】10、Why deep?(待填坑)
【李宏毅机器学习笔记】11、 Semi-supervised
【李宏毅机器学习笔记】 12、Unsupervised Learning - Linear Methods
【李宏毅机器学习笔记】 13、Unsupervised Learning - Word Embedding(待填坑)
【李宏毅机器学习笔记】 14、Unsupervised Learning - Neighbor Embedding(待填坑)
【李宏毅机器学习笔记】 15、Unsupervised Learning - Auto-encoder(待填坑)
【李宏毅机器学习笔记】 16、Unsupervised Learning - Deep Generative Model(待填坑)
【李宏毅机器学习笔记】 17、迁移学习(Transfer Learning)
【李宏毅机器学习笔记】 18、支持向量机(Support Vector Machine,SVM)
【李宏毅机器学习笔记】 19、Structured Learning - Introduction(待填坑)
【李宏毅机器学习笔记】 20、Structured Learning - Linear Model(待填坑)
【李宏毅机器学习笔记】 21、Structured Learning - Structured SVM(待填坑)
【李宏毅机器学习笔记】 22、Structured Learning - Sequence Labeling(待填坑)
【李宏毅机器学习笔记】 23、循环神经网络(Recurrent Neural Network,RNN)
【李宏毅机器学习笔记】 24、集成学习(Ensemble)
------------------------------------------------------------------------------------------------------
【李宏毅深度强化学习】视频地址:https://www.bilibili.com/video/av10590361?p=18
课件地址:http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML17_2.html
-------------------------------------------------------------------------------------------------------
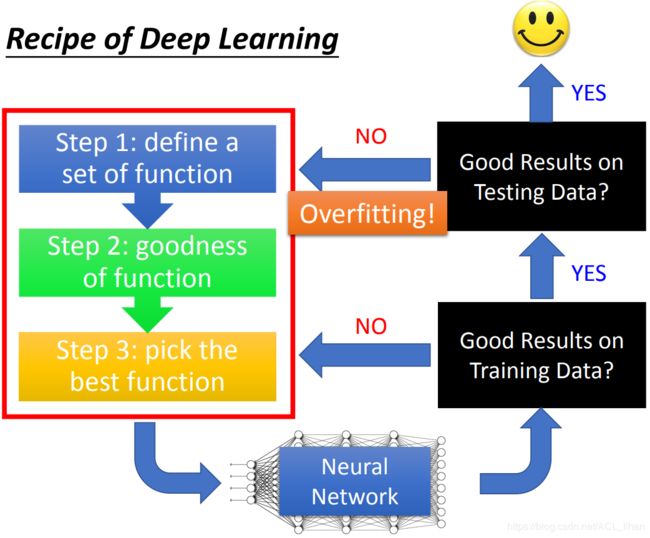
深度学习过程
- 经过熟悉的机器学习的三个步骤,得到一个Neural Network
- 看它在训练集上的表现。表现不好的话继续回去训练;表现好的话去测试集
- 看它在测试集上的表现。如果训练集表现好,而测试集表现不好的话说明发生overfitting,要重新设计模型;如果训练集测试集都表现好,就完成任务。
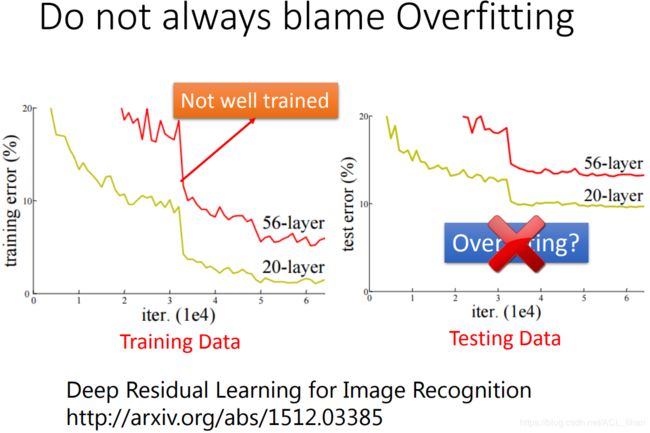
不要什么都归咎于overfitting
上面说过,在testing data表现不好有可能是发生overfitting,但这个的前提model在training data表现好。
而像上图的例子,56层的model在training data 就已经输给20层的model(有可能56层的model卡在local minima),所以这时在testing data上,56层的model输给20层的model就不是overfitting。
本节课讲到的方法概括
在training data上表现不佳,可以用New activation function、Adaptive Learning Rate。
在testing data上表现不佳,可以用Early Stopping、Regularization、Dropout。
下面对它们具体讲解。
New activation function
Hard to deep
上图是使用sigmoid function作为activation function,对网络进行加深的结果。
可以看到,在9层开始,准确率突然降了很多。
理论上越深的网络,能力越强,为什么上图的结果好像和这句话矛盾的?是因为网络发生了Vanishing Gradient Problem。
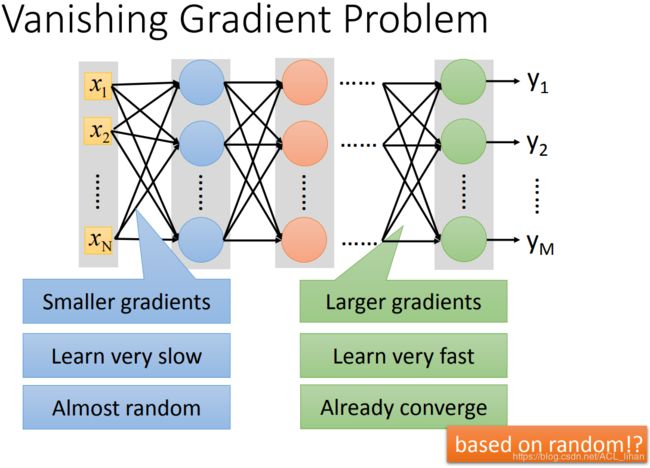
Vanishing Gradient Problem
当网络叠得很深的时候,靠近输入层的那几层的参数,对最后的loss function的微分很小(gradient比较小)。 靠近输出层的那几层的参数,对最后的loss function的微分比较大(gradient比较大)。
举个例子:
现在随机初始化参数。经过一段时间的训练,靠近input layer的参数的更新量很小,接近于没有(因为gradient很小)。而靠近output layer的参数则已经收敛到最低点。这样就变成只有靠近output layer的那几层的参数有更新到好的效果,而靠近input layer的参数则接近完全没有更新,还是初始化的那些随机数。
导致Vanishing Gradient Problem是因为使用了sigmoid function。
我们知道,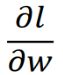 (gradient)其实等价于
(gradient)其实等价于 ![]() 对最后的
对最后的![]() 的影响。 gradient大,
的影响。 gradient大,![]() 对
对![]() 的影响就大。
的影响就大。
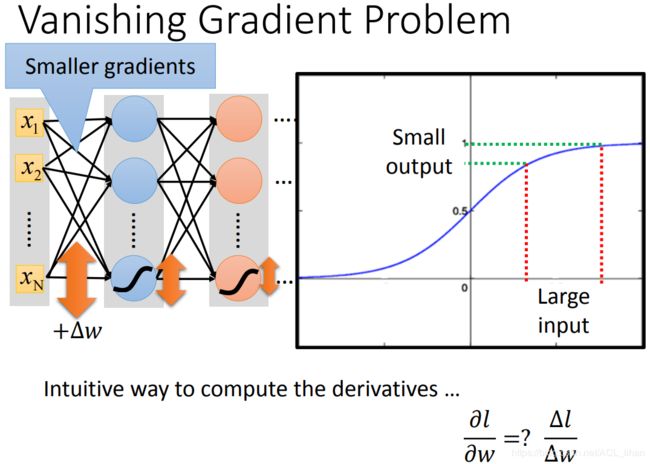
从上图可以看到,sigmoid function在远离(0,0)的地方,斜率变得很小。这样即便 input 的![]() 很大, output的
很大, output的 ![]() 也不见得有那么大。更何况还经过多层的sigmoid function的多次衰减,所以最后反映到对
也不见得有那么大。更何况还经过多层的sigmoid function的多次衰减,所以最后反映到对 ![]() 的影响就变得更小了。
的影响就变得更小了。
所以这就是为什么靠近input layer的参数的gradient会比较小,而靠近output layer的参数的gradient会比较大。
为了解决这个问题,可以把activation function改成ReLU。
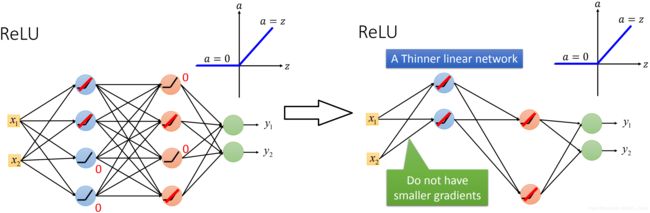
ReLU
在 x<0 的区间,ReLU的输出值都等于0 。 在 x>0 的区间,ReLU的输出值都等于输入值。
如上图,当ReLU的输入值小于0,可以等同于这个神经元直接删掉。就从左图变成右图的样子。
这时所有的Nueron都是input=output ,就不存在刚才sigmoid function那样逐层衰减的问题。
RELU是分段线性函数,怎么实现非线性呢?
答:ReLu虽然在大于0的区间是线性的,在小于等于0的部分也是线性的,但是当这两部分合起来,得到的却是非线性函数。对于浅层的机器学习,比如经典的三层神经网络,用它作为激活函数的话,那表现出来的性质肯定是线性的。但是在深度学习里,少则几十,多则上千的隐藏层,虽然,单独的隐藏层是线性的,但是很多的隐藏层表现出来的就是非线性的。
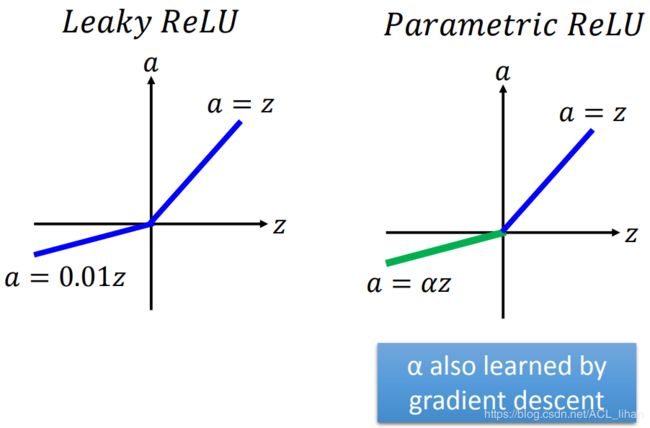
ReLU - varian
如上图所示,就是Leaky ReLU和 Parametric ReLU(其中的![]() 也是需要通过训练得出的)
也是需要通过训练得出的)
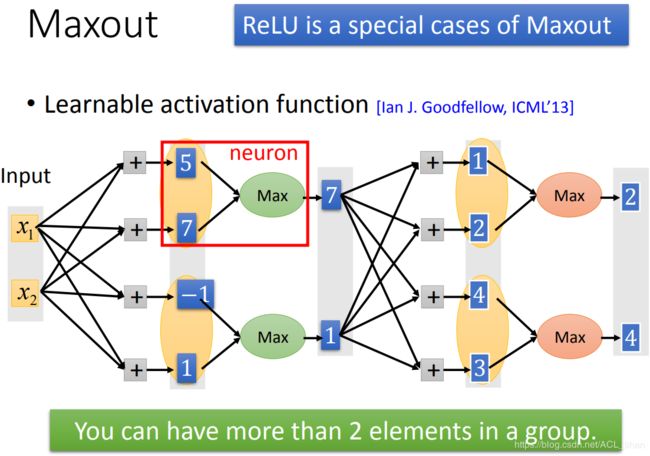
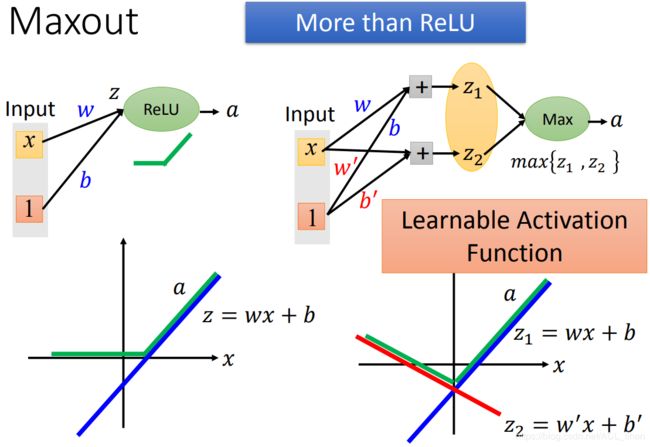
Maxout
在Maxout这个方法中,activation function是直接由网络自己去学出来的,所以ReLU也可以说是Maxout其中的一个特殊例子(等下会细讲怎么模拟出ReLU)。
Maxout的做法是这样:把原来要输入到activation function的值(比如上图的5,7,-1,1),把它们分组(多少个为一组是你决定的,如图为2个一组),然后选择一个大的值作为输出。
这里,可以把图中红框的地方看成是一个Neuron。
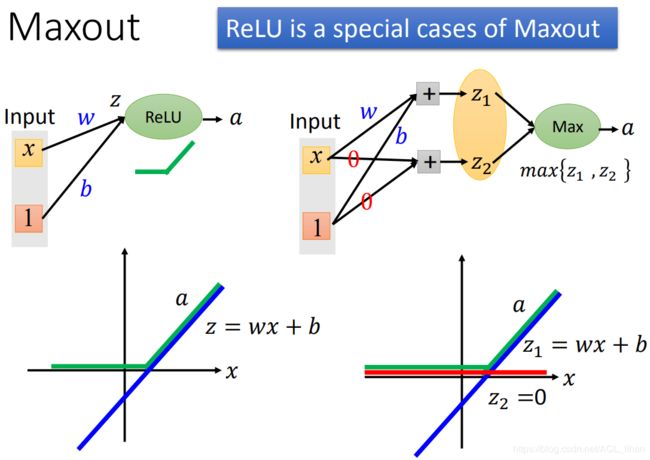
刚才说过Maxout能模拟出ReLU。这里具体看下。
调整Maxout的其中一个输入 ![]() 的weight 和bias,使它的图像如上图蓝线所示。
的weight 和bias,使它的图像如上图蓝线所示。
当Maxout的其中一个输入 ![]() 的weight和bias都为0,这样
的weight和bias都为0,这样![]() 就一直为0,如上图红线所示。
就一直为0,如上图红线所示。
这样两个输入通过Maxout后,就变成ReLu的样子,如上图绿线所示。
像模拟出ReLU一样,如上图所示,只要再改变weight和bias,还能模拟出更多不同Activation Function 。
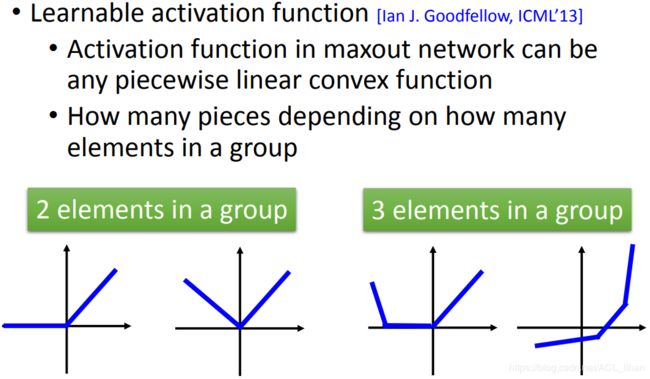
How many pieces depending on how many elements in a group
如上图所示,在Maxout中,一个group里有多少个elements,就反映了最后学出来的Activation Function 有多少“段”。
Maxout - Training
Maxout只输出大的那个值,如图,![]() 得到输出;而
得到输出;而 ![]() 则没有输出,就是说
则没有输出,就是说![]() 等同于没用到。所以这里只train了 连接到
等同于没用到。所以这里只train了 连接到 ![]() 的参数,而没train连接到
的参数,而没train连接到 ![]() 的参数。
的参数。
问题:只train了连到 ![]() 的参数,而没train到连接到
的参数,而没train到连接到 ![]() 的参数,这会不会不好?
的参数,这会不会不好?
答:不会,因为在实做中,是有很多不同的input,就会导致每次Maxout的输出是不一样的。就是说有可能不同的input,会导致![]() 得到输出;而
得到输出;而 ![]() 则没有得到输出。这时连接到
则没有得到输出。这时连接到 ![]() 的参数就可以被进行train了。
的参数就可以被进行train了。
Adaptive Learning Rate
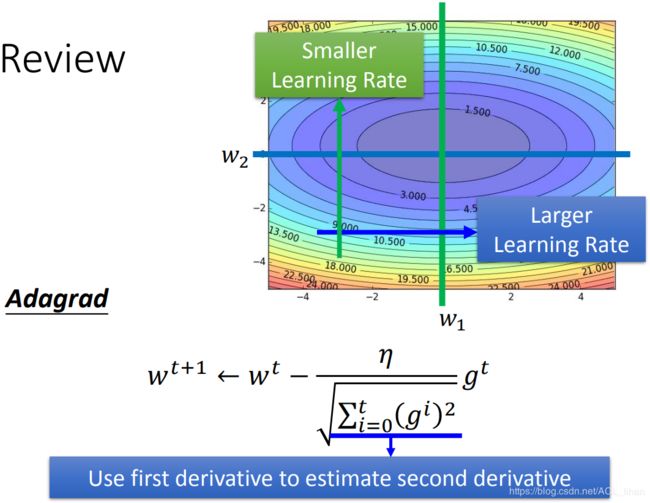
Review
之前说过,如上图,不同方向的gradient是不同。这时使用Adagrad的方法,就会对不同方向给出不同的learning rate。
gradient大的方向,learning rate就大 。gradient小的方向,learning rate小 。
在deep learning中,error surface会变得更复杂。这时使用 Adagrad 已经不够了,所以下面将介绍3中新的方法,分别是RMSProp、Momentum、Adam 。
RMSProp
在刚才Adagrad的回顾中,我们知道Adagrad的learning rate是长这样 ,分子是之前所有gradient的均方根。
,分子是之前所有gradient的均方根。
而RMSProp中learning rate变成 ![]() ,
,![]() 同样包括之前所有gradient的均方根,只是这里对新的gradient和旧的gradient有给出不同的权重,做法如下:
同样包括之前所有gradient的均方根,只是这里对新的gradient和旧的gradient有给出不同的权重,做法如下:
这个式子中,![]() 越小,代表越倾向于相信此时算出来的新的gradient所告诉你的error surface的陡峭程度;而
越小,代表越倾向于相信此时算出来的新的gradient所告诉你的error surface的陡峭程度;而![]() 越大,则代表越倾向于相信以往算出来的gradient 。
越大,则代表越倾向于相信以往算出来的gradient 。
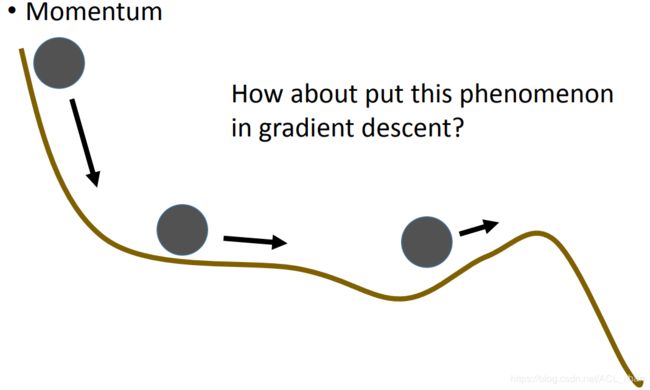
Momentum
现实世界中,一个球由高处往地处走,到达最低点后并不会直接停下来,可能会由于惯性的影响再移动一点。所以就想到把惯性的因素也考虑进gradient descent里面,就不会因为遇到local minima而直接卡主。
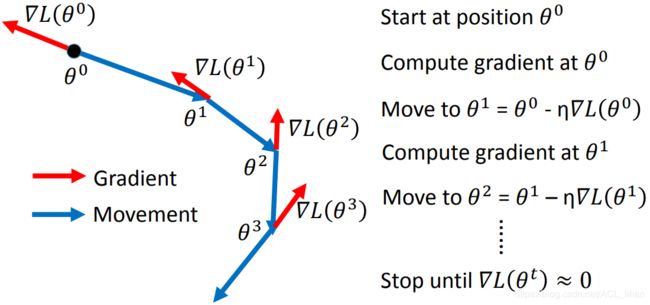
Review: Vanilla Gradient Descent
如上图,在 Vanilla Gradient Descent的方法中,红色代表算出的gradient的方向,蓝色则代表要移动的方向,移动的方向是和gradient的方向正好相反的。
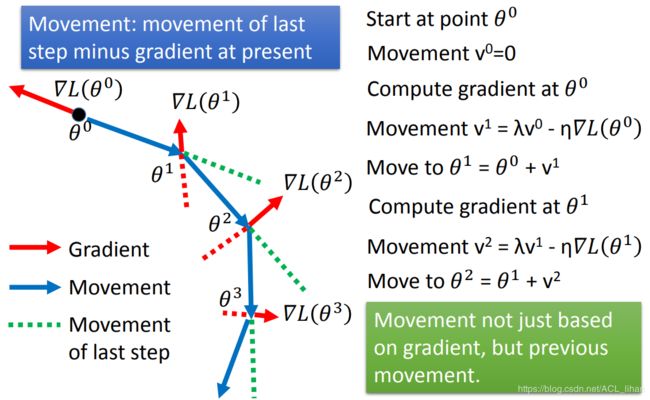
Momentum
如上图,红色是gradient的方向,绿色是上一步movement的方向,考虑这两者的影响,就形成最终的movement(蓝色)。
在 Momentum 中,参数的更新公式加入了新的一项,即上一步的移动所产生的影响。
以另一个角度来看,其实 ![]() 就是之前所有的gradient的加权总和。越久远的gradient对现在产生的影响越小 。
就是之前所有的gradient的加权总和。越久远的gradient对现在产生的影响越小 。
红色代表gradient告诉我们要移动的方向,绿色代表惯性的方向,蓝色则是最终的移动方向。
可以看到加了惯性之后,有可能就能凭借惯性直接冲出local minima。
Adam
把刚才讲的RMSProp 和 Momentum 结合起来,就形成Adam。
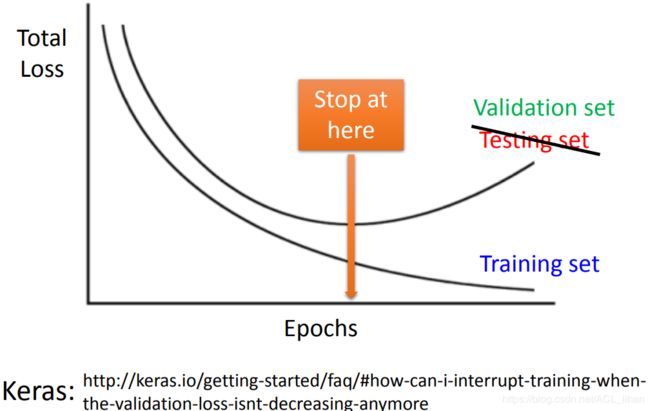
Early Stopping
在使用training set 进行训练的时候,同时使用validation set 来查看total loss的情况。
即便training set上的loss一直变低,只要validation set上的loss值开始出现增长时,就要提前结束训练。
Regularization
L2 Regularization
在原来的Loss Function后再加上一项正则项,使它变成一个新的Loss Function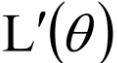 。
。
所以的Loss Function变成两项,不仅要最小化原来的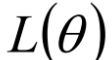 ,还要最小化
,还要最小化 。
。
由于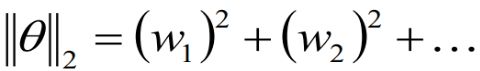 ,所以对它做关于
,所以对它做关于 ![]() 的偏微分,结果为
的偏微分,结果为 ![]() 。再因为
。再因为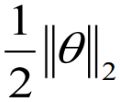 ,所以正则项的微分结果为
,所以正则项的微分结果为![]() 。
。
参数更新公式进行整理后如上图所示。由于 learning rate 和 ![]() 通常会设很小。所以
通常会设很小。所以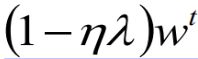 ,就类似于 w 每次都是乘上0.99,这样经过多次更新以后,w就会越来越接近0 。 当然,整个式子到最后不会真的变成0,因为还有一项
,就类似于 w 每次都是乘上0.99,这样经过多次更新以后,w就会越来越接近0 。 当然,整个式子到最后不会真的变成0,因为还有一项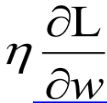 。
。
L1 Regularization
原来 L2 Regularization 的每一项weight是二次方再求和。而L1 Regularization 的每一项weight就是取绝对值后直接求和。
如果![]() 是正的,对
是正的,对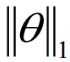 求关于
求关于![]() 的偏微分就是1;如果
的偏微分就是1;如果![]() 是负的,对
是负的,对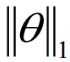 求关于
求关于![]() 的偏微分就是-1;
的偏微分就是-1;
把参数更新的公式整理一下,如图倒数第二行所示(倒数第一行是L2 Regularization)。
可以看出L1 Regularization的方式相比于L2 Regularization僵硬。举个例子:
- 初始化的w是10000,现在目标要使 w 更新到接近0 。
- L1每次更新时都减去10,下降速度是固定的。这样在 w 大的时候,下降慢;在 w 已经变得很小(比如0.8)的时候,则会出现下降过快的情况。
- 而L2每次乘0.99,这样在初始值比较大的时候,L2下降的快,当w比较小时,又会下降的比较慢。
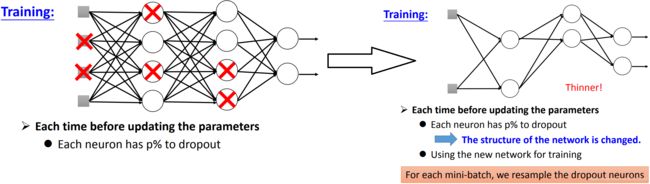
Dropout
每个Neuron有 p% 的概率会被丢掉,丢掉后和这个Neuron相连的weight也就没用了。
丢掉后,网络的结构就变成右边的样子。
训练时数据时拆成很多个batch,使用新的batch去训练前,需要先重新Dropout一下,形成新的网络结构,再去训练。
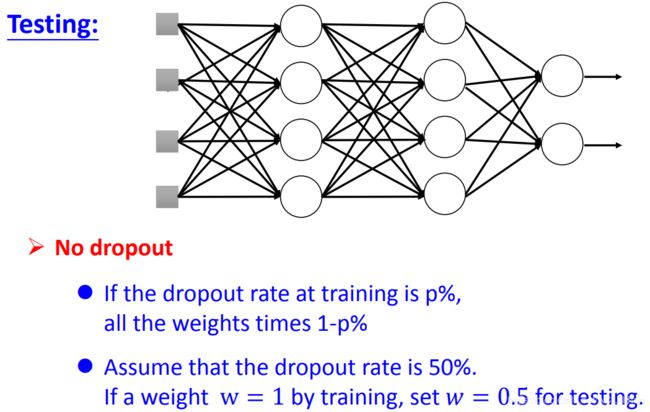
- 在testing阶段,不用使用Dropout。
- 如果Dropout的比例为p%,则所有的weight要乘上1-p%。