【数值分析】用matlab解决插值问题、常微分方程初值问题
- 一、
- 二、
- 三、
- 四、
一、
- 问题描述：已知 sin(0.32)=0.314567, sin(0.34)=0.333487, sin(0.36)=0.352274，
sin(0.38)=0.370920。请采用线性插值、二次插值、三次插值分别计算 sin(0.35)的值。 - 算法设计：
function yint = lagrange(x,y, xx)
%UNTITLED x和y分别存放已知点的x和y值的数组，xx指的是待插值点的坐标
%多项式的次数由输入向量x的长度决定，如果输入了n个值，那么插值多项式的次数就是n-1.
% x和用y从下面数据中选择x = [0.32,0.34,0.36,0.38],
% y=[0.314567,0.333487,0.352274,0.370920]
n = length(x);
if length(y) ~= n
error('x and y must be same length');
end
s = 0;
for i = 1:n
product = y(i);
for j = 1:n
if i~=j
product = product *(xx-x(j))/(x(i)-x(j));
end
end
s = s + product;
end
yint = s;
end- 数值实验：
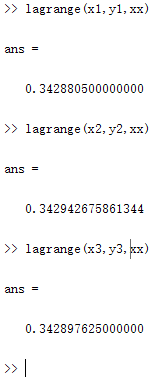
1、建立了3个数组，长度分别为2，3，4分别对应线性插值，二次插值和三次插值。
| 插值类型 | x向量 | y向量 | 插值点xx | 插值结果 |
|---|---|---|---|---|
| 线性插值 | x1 = [0.34,0.36]； | y1= [0.333487,0.352274]； | 0.35 | 0.3428805 |
| 二次插值 | x2 = [34,0.36,0.38]； | y2 = [0.333487,0.352274,0.370920]; | 0.35 | 0.342942675861344 |
| 三次插值 | x3 = [0.32,0.34,0.36,0.38]; | y3=[0.314567,0.333487,0.352274,0.370920]; | 0.35 | 0.342897625 |
- 结果分析：
二、
- 问题描述：请采用下述方法计算 115 的平方根，精确到小数点后六位。
（1）二分法。选取求根区间为[10, 11]。
（2）牛顿法。
（3）简化牛顿法。
（4）弦截法。
绘出横坐标分别为计算时间、迭代步数时的收敛精度曲线。 - 算法设计：
（1）二分法。
function [ root, time, itenum ] = bisect( num, xl, xu)
%UNTITLED2 num是要求平方根的数字，xl是已知下届，xu是已知上界
% root是最终求得的平方根，time是所花时间，itenum是迭代步数。
if nargin < 3
error(' at least 3 input arguments required');
end
itenum = 0;
tic;
yl = xl*xl - num;
yu = xu*xu - num;
ym = ((xl+xu)/2)*((xl+xu)/2) - num;
if yl*yu >0
error('no sign changed');
end
while(1)
itenum = itenum +1;
if ym == 0 || xu - xl < 0.0000001
break;
end
test = yu*ym;
if test > 0
xu = (xl+xu)/2;
else
xl = (xl+xu)/2;
end
yu = xu*xu - num;
ym = ((xl+xu)/2)*((xl+xu)/2) - num;
end
time = toc;
root = (xl+xu)/2;
end
（2）牛顿法。
function [ root, time, itenum ] = newton( num,xs)
%UNTITLED3 num是要求平方根的数字，xs是平方根的估计值
% root是求得的平方根，time是所用时间，itenum是迭代步数
x0 = xs;
ite = 0;
tic;
while(1)
x1 = (x0+num/x0)/2;
ite = ite + 1;
if abs(x1-x0) < 0.0000001
break;
end
x0 = x1;
end
root = x1;
itenum = ite;
time = toc;
end（3）简化牛顿法。
function [ root, time, itenum ] = simpleNewton( num,xs)
%UNTITLED3 num是要求平方根的数字，xs是平方根的估计值
% root是求得的平方根，time是所用时间，itenum是迭代步数
x0 = xs;
ite = 0;
tic;
while(1)
x1 = x0-(x0*x0 - num)/(2*xs);
ite = ite + 1;
if abs(x1-x0) < 0.0000001
break;
end
x0 = x1;
end
root = x1;
itenum = ite;
time = toc;
end（4）弦截法。
function [ root, time, itenum ] = secant( num,x_1,x0)
%UNTITLED3 num是要求平方根的数字，x_1和x是两个估计值
% root是求得的平方根，time是所用时间，itenum是迭代步数
xk = x0;
xk_1 = x_1;
ite = 0;
tic;
while(1)
xk1 = xk-(xk*xk - num)*(xk - xk_1)/( (xk*xk - num) - (xk_1*xk_1 - num) );
ite = ite + 1;
if abs(xk1-xk) < 0.0000001
break;
end
xk_1 = xk;
xk = xk1;
end
root = xk1;
itenum = ite;
time = toc;
end- 数值实验：
下面所有结果中，root表示求得的115的平方根，time是算法执行时间，itenum是算法迭代次数。
（1）二分法。
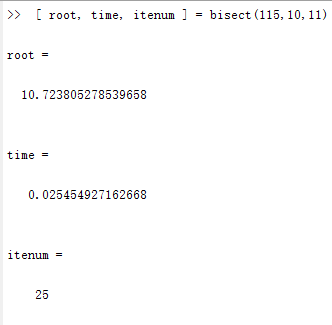
（2）牛顿法。
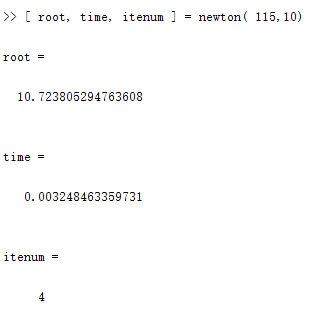
（3）简化牛顿法。
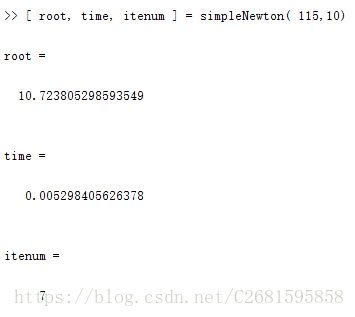
（4）弦截法。
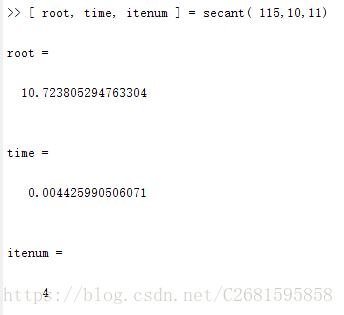
- 结果分析：
从上面的结果可以看出，达到相同的精度，二分法执行的时间和步数都是最多的。而牛顿法和弦截法所用步数相等，但牛顿法所用时间更短，简化牛顿法计算速度处于二分法和牛顿法及弦截法中间，但它的计算更简单。下面用更加直观的曲线图来说明这几种算法的执行效率。
考虑到各个算法的执行步数都比较少，所以以时间为横轴的图就直接再每一步时纪录其时间，然后绘图。
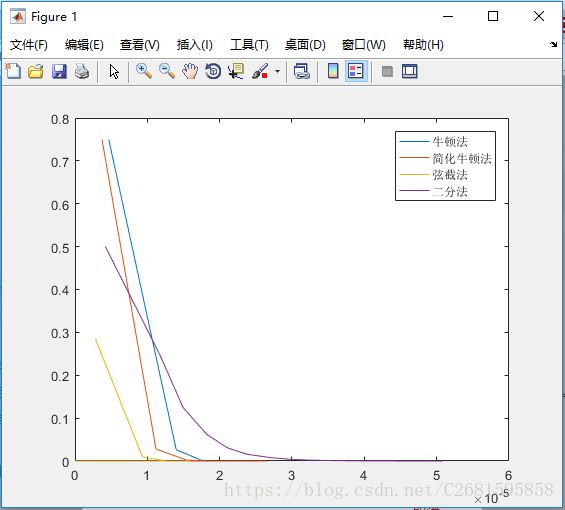
然后以执行步数为横轴，收敛精度为纵轴在来画图。
三、
- 问题描述：
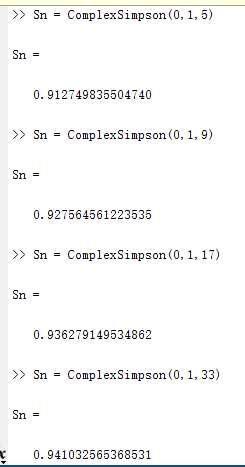
请采用复合梯形公式与复合辛普森公式，计算 sin(x)/x 在[0, 1]范围内的积分。采样
点数目为 5、9、17、33。 - 算法设计：
（1）复合梯形公式
function Tn = CompositeTrapezoidal(a,b,n )
%UNTITLED10 a为区间下界，b为区间上界，n为区间等份
% Tn是积分结果
h = (b-a)/n;
sum = 0;
for k = 1:n-1
xk = a + k*h;
sum = sum + sin(xk)/xk;
end
Tn = h*(sin(b)/b + 2*sum)/2;
end（2）复合辛普森方法
function Sn = ComplexSimpson(a,b,n)
%UNTITLED10 a为区间下界，b为区间上界，n为区间等份
% Sn是积分结果
h = (b-a)/n;
sum1 = 0;
for k = 1:n-1
xk = a + k*h;
sum1 = sum1 + sin(xk)/xk;
end
sum2 = 0;
for k = 0:n-1
xk = a + k*h;
xk12 = xk + h/2;
sum2= sum2 + sin(xk12)/xk12;
end
Sn = h*(sin(b)/b + 2*sum1 + 4*sum2)/6;
end
- 数值实验：
复合梯形公式：
复合辛普森公式：
- 结果分析：
四、
- 问题描述：
请采用下述方法，求解常微分方程初值问题 y’=y-2x/y，y(0)=1，计算区间为[0, 1]，
步长为 0.1。
（1）前向欧拉法。
（2）后向欧拉法。
（3）梯形方法。
（4）改进欧拉方法 - 算法设计：
（1）前向欧拉法。
function [result] = Euler(x0, y0, h)
%x0, y0是初值，h是步长
result = zeros(0,10);
xn = x0;
yn = y0;
for n = 1:10
yn1 = yn + h*(yn - 2*xn/yn);
xn = xn + h;
yn = yn1;
result(n) = yn1;
end
end（2）后向欧拉法。
function [ results ] = BackwardEuler(x0, y0 ,h , itenum)
%x0, y0是初值，h是步长， itemnum是迭代次数
results = zeros(0,10);
xn = x0;
yn = y0;
yn10 = y0 + h*(y0 - 2*x0/y0);
for n = 1:10
xn = xn + h;
for m = 1:itenum
yn11 = yn + h*(yn10 - 2*xn/yn10);
yn10 = yn11;
end
yn = yn11;
yn10 = yn + h*(yn - 2*xn/yn);
results(n) = yn11;
end
end（3）梯形方法。
function [ results ] = Trapezoidal (x0,y0,h, itenum)
%x0, y0是初值，h是步长， itemnum是迭代次数
results = zeros(0,10);
xn = x0;
yn = y0;
yn10 = y0 + h*(y0 - 2*x0/y0);
for n = 1:10
xn = xn + h;
for m = 1:itenum
yn11 = yn + h*((yn - 2*(xn - h)/yn)+(yn10 - 2*xn/yn10))/2;
yn10 = yn11;
end
yn = yn11;
yn10 = yn + h*(yn - 2*xn/yn);
results(n) = yn11;
end
end（4）改进欧拉方法
function [ results ] = ImprovedEuler (x0,y0,h )
%x0, y0是初值，h是步长
results = zeros(0,10);
xn = x0;
yn = y0;
yn10 = y0 + h*(y0 - 2*x0/y0);
for n = 1:10
xn = xn + h;
yn11 = yn + h*((yn - 2*(xn - h)/yn)+(yn10 - 2*xn/yn10))/2;
yn = yn11;
yn10 = yn + h*(yn - 2*xn/yn);
results(n) = yn11;
end
end- 数值实验：
（1）前向欧拉法。
（2）后向欧拉法。
（3）梯形方法。
（4）改进欧拉方法
- 结果分析：
从上面结果可以看出，梯形方法和改进欧拉方法的计算结果精度明显高于欧拉方法和后退欧拉方法。