机器学习：朴素贝叶斯代码实现（不调库，基于《统计学习方法》中的简单数据）

什么是朴素贝叶斯：

1. 《统计学习方法》中，李航老师简洁地介绍了朴素贝叶斯基础的原理和算法
   虽然通篇下来也是满满的公式，但基本都是上层的公式，省略了许多底层的推导
   例如：极大似然估计法推出朴素贝叶斯法中的先验概率估计公式？
   总的来说对新手十分友好，建议入门之选。

2. “朴素”一词，到底是何意思？
   在贝叶斯公式的基础上，朴素贝叶斯方法做了一个强假设，对于一个结果的发生（y）
   导致其发生的因素为x ( x = (x1, x2, …, xn)), 我们认为其中x1,…,xn是n个互相独立的小事件
   也就是每一个都对y的发生有影响，但他们之间却相互无影响。
   

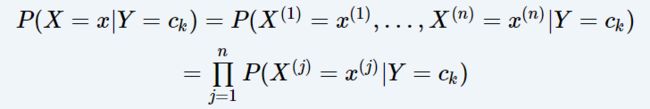
贝叶斯估计 和 极大似然估计：

对于大多数初学者，基本都会对贝叶斯产生理解上的困惑

• 这里放一篇文章，从数学角度详细解释了两者的原理：贝叶斯估计、最大似然估计、最大后验概率估计

如果你觉得又臭又长不想看，我简单通俗说明一下他们之间思想的不同之处：

• 首先你要明白，朴素贝叶斯法 和 贝叶斯估计 是两个不同的东西
  贝叶斯估计 和 极大似然估计 都是 朴素贝叶斯法 中用来计算先验概率的方法
  极大似然估计：简单来说就是中学阶段接触的简单概率，一枚硬币抛100次，40次向上，我们就认为此硬币抛出向上的概率为2/5，因为这个概率是最支持当前结果的（极大似然的核心思想），于是你可以发现，极大似然法得到的参数是完全被数据所支配的。而概率这种东西，总是会有偏差的。
  下图是极大似然估计的先验概率
  
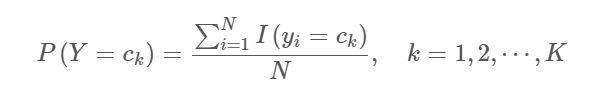
  贝叶斯估计：如之前所说，任何数据集，总是带有片面性的，不全面的。所以最终参数总是存在偏差的，不能把最支持对当前结果的模型作为当前事件的概率模型，于是贝叶斯估计中认为参数是变化的而不是固定的。回忆一下贝叶斯公式，它是用来计算后验概率的，也就是已知结果求其导致原因的概率。该公式的结果取决于两方面：似然估计和先验概率。正是如此，我们最终的估计结果才更加客观合理地反映模型的参数。对于上面抛硬币的例子，贝叶斯估计的概率也或许就变成是（2 + N）/ （5 + M）
  下图是贝叶斯估计的先验概率
  

---

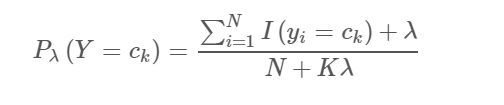
代码实现：（使用极大似然估计）

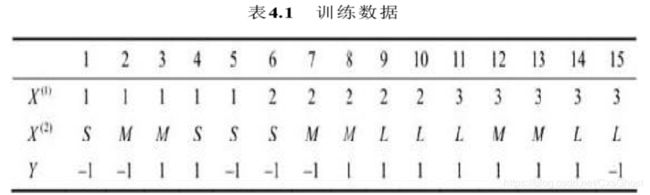
对于以下数据的简单代码实现，但不仅限于此数据，扩展以下数据，使其变成多分类，增大数据量，依然可以用本代码来进行预测。

分步解析

1. 数据量比较小，就直接手动输入了，用字典来存储先验概率，便于后续计算时的调用

class Bayes:
    def __init__(self):
        self.t_data = np.array([[1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3],
                                ['S', 'M', 'M', 'S', 'S', 'S', 'M', 'M', 'L', 'L', 'L', 'M', 'M', 'L', 'L'],
                                [-1, -1, 1, 1, -1, -1, -1, 1, 1, 1, 1, 1, 1, 1, -1]])
        self.p_y = {}
        self.p_x1_y = {}  
        self.p_x2_y = {}

2. 统计y的种类及数量，用于后续计算
   使该二维分类器不局限于两种类（y），接下来先统计y的种类，并计算P(Y=c)的先验概率，再切分训练数据
   计算先验概率并对应y值存入字典，然后根据不同的y切分数据，各自存入一个列表，这些列表存于字典ys

   
    def train_1(self):
        count_y = Counter(self.t_data[2])  
        ys = {} 
        for y in count_y.keys():
            ys[y] = []
            self.p_y[y] = count_y[y] / len(self.t_data[0])  # 计算先验概率并对应y值存入字典
        for i in range(len(self.t_data[0])): # 遍历数据，根据其y存入对应列表
            ys[self.t_data[2][i]].append(self.t_data[:, i])  
        print('数据切分完成，计算其余先验概率...')
        for item in ys.items():
            self.train_2(item)
        print('学习完毕！可以开始预测')

3. 因为切分后数据是列表形式，先转化为矩阵，然后计算P(X=a|Y=c)的先验概率，统计每个特征的值的种类，然后计算，并直接以照特征值和y值组成key，把计算结果存入字典
   train_2在上方train_1中调用

    def train_2(self, _y):
        data = np.array(_y[1])  # 先把数据转化为矩阵，便于接下来切片统计运算
        count_x1 = Counter(data[:, 0])
        count_x2 = Counter(data[:, 1])
        for x1 in count_x1.keys():  # 计算相应的概率，存入字典
            self.p_x1_y['{}_{}'.format(x1, _y[0])] = count_x1[x1] / len(data)
        for x2 in count_x2.keys():
            self.p_x2_y['{}_{}'.format(x2, _y[0])] = count_x2[x2] / len(data)

4. 预测：对于相同的输入，可能出现多种不同预测结果（后验概率相同），要对此做处理。虽然对此次数据作用不大，但是对于扩展数据（比如多分类数据），会很有作用。

 def analyse_input(self):  # 计算后验概率并比较
        in_data = input('输入x1, x2（空格隔开）：').split(' ')
        p_p = 0
        result = []
        for j in self.p_y.keys():
            pp = self.p_y[j] * self.p_x1_y['{}_{}'.format(in_data[0], j)] *\
                 self.p_x2_y['{}_{}'.format(in_data[1], j)]
            if pp >= p_p:  
                if pp > p_p:  # 若有出现更大的概率，需要把先前已有的所有结果全部替换
                    if not result:  # 开始的时候列表是空的，如果只写循环替换，其实那个循环根本不会开始。
                        result.append(j)  # 所以必须额外加这一个判断（其实我觉得我这里搞麻烦了。。但是也没想到什么好的解决办法）
                    else:
                        for r in range(len(result)):
                            result[r] = j
                elif p_p == pp:
                    result.append(j)
                p_p = pp
        result = list(set(result))
        if len(result) == 1:
            print('预测结果为：{}'.format(result[0]))
        else:
            print('可能结果为以下几种：', end='')
            for e in result:
                print(e)

完整代码：

import numpy as np
from collections import Counter


class Bayes:
    def __init__(self):
        self.t_data = np.array([[1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3],
                                ['S', 'M', 'M', 'S', 'S', 'S', 'M', 'M', 'L', 'L', 'L', 'M', 'M', 'L', 'L'],
                                [-1, -1, 1, 1, -1, -1, -1, 1, 1, 1, 1, 1, 1, 1, -1]])
        self.p_y = {}
        self.p_x1_y = {}  # 使用字典方便计算时调用
        self.p_x2_y = {}

    def train_1(self):
        count_y = Counter(self.t_data[2])  # 统计y的种类及数量，用于后续计算
        ys = {}  # 使该二维分类器不局限于两种类（y）（不失一般性），接下来先统计y的种类，并计算概率，再切分训练数据
        for y in count_y.keys():
            ys[y] = []
            self.p_y[y] = count_y[y] / len(self.t_data[0])  # 计算先验概率并对应y值存入字典
        for i in range(len(self.t_data[0])):
            ys[self.t_data[2][i]].append(self.t_data[:, i])  # 将数据切分后分别存入字典中的列表，key是对应的y值
        print('数据处理完成，开始学习...')
        for item in ys.items():
            self.train_2(item)
        print('学习完毕！可以开始预测')

    def train_2(self, _y):
        data = np.array(_y[1])  # 先把数据转化为矩阵，便于接下来切片统计运算
        count_x1 = Counter(data[:, 0])
        count_x2 = Counter(data[:, 1])
        for x1 in count_x1.keys():  # 计算相应的概率，存入字典
            self.p_x1_y['{}_{}'.format(x1, _y[0])] = count_x1[x1] / len(data)
        for x2 in count_x2.keys():
            self.p_x2_y['{}_{}'.format(x2, _y[0])] = count_x2[x2] / len(data)

    def analyse_input(self):  # 计算后验概率并比较
        in_data = input('输入x1, x2（空格隔开）：').split(' ')
        p_p = 0
        result = []
        for j in self.p_y.keys():
            pp = self.p_y[j] * self.p_x1_y['{}_{}'.format(in_data[0], j)] *\
                 self.p_x2_y['{}_{}'.format(in_data[1], j)]
            if pp >= p_p:  # 观察到，对于相同的输入，可能出现两种不同预测结果（对于本次数据来说，只有两种结果），要对此做处理
                if pp > p_p:  # 若有出现更大的概率，需要把先前已有的所有结果全部替换
                    if not result:  # 开始的时候列表是空的，如果直写循环替换，其实那个循环根本不会开始。如果在循环后添加，那将会导致接下来有的结果会重复进入列表（被替换的和被添加的）
                        result.append(j)  # 所以必须额外加这一个判断（其实我觉得我这里搞麻烦了。。但是也没想到什么好的解决办法）
                    else:
                        for r in range(len(result)):
                            result[r] = j
                elif p_p == pp:
                    result.append(j)
                p_p = pp
        result = list(set(result))
        if len(result) == 1:
            print('预测结果为：{}'.format(result[0]))
        else:
            print('可能结果为以下几种：', end='')
            for e in result:
                print(e)


b = Bayes()
b.train_1()
b.analyse_input()