微分方程与差分方程
微分方程与差分方程
详细内容可以参见 Github 博客
当我们需要对象的某些特性随时间演变的过程,分析其本质规律并预测他的未来性态、研究他的控制手段时,通常要建立对象的动态模型。
所以需要预测并控制的模型基本得用微分方程建模,其中又以传染病模型应用最广
另外可尝试系统动力学建模,还有网上看到的自动驾驶预测控制 文章
将微分方程离散化便得到差分方程,但也有一些实际问题直接用差分方程的模型更为方便
与常微分方程课程中的动态模型不同的是数模中的系统假设事先是未知的,不同的假设给出不同的模型,事先没有答案,需要寻求最好的。
传染病模型
SI 模型
假设条件
-
考察地区内总人数 N N N 不变,既不考虑生死也不考虑迁移。人群分为易感染者(Susceptible)和已感染者(Infective),此两类人所占的比例分别记为 s ( t ) , i ( t ) s(t),i(t) s(t),i(t) 。
-
每个人每天有效接触的平均人数为 λ \lambda λ ,称为日接触率
从时间 Δ t \Delta t Δt 内接触率为 λ Δ t \lambda \Delta t λΔt
可得模型
d i d t = λ i ( 1 − i ) , i ( 0 ) = i 0 \frac{ \mathrm{d}i}{\mathrm{d}t}=\lambda i(1-i),i(0)=i_0 dtdi=λi(1−i),i(0)=i0
此即 logistic 模型。当 i i i=0.5 时,增长速度最快(S型增长)。增长最快的时间
t m = λ − 1 ln ( 1 i 0 − 1 ) t_m=\lambda^{-1}\ln(\frac{1}{i_0}-1) tm=λ−1ln(i01−1)
此模型中所有人必将感染,因为没有考虑治愈。这同样有重大用途,适用于哪些势不可挡的趋势演变,比如新能源取代旧燃油车的过程
新能源汽车的比列即 i ( t ) i(t) i(t) ,车主的相互交流与宣传表征了传染的过程,最终新能源汽车将完全替代燃油车
SIS 模型
新增假设:
- 每天被治愈的病人数占
- h与病人总数的比列为 μ \mu μ ,定义 σ = λ μ \sigma=\frac{\lambda}{\mu} σ=μλ 表示整个传染过程中每个病人有效接触的平均人数。
d i d t = λ i ( 1 − i ) − μ i = , i 0 = i ( 0 ) \frac{ \mathrm{d}i}{\mathrm{d}t}=\lambda i(1-i)-\mu i= ,i_0=i(0) dtdi=λi(1−i)−μi=,i0=i(0)
具体参数分析略,但是有一个注意点:
仅仅从导函数并不能完全刻画原函数的增减信息,很有可能有极限点的存在而导致分支
SIR 模型
大多数传染病如天花、流感等治愈后既非健康者也非传染者,而以退出传染系统
可用于刻画存在第三方干扰的二元竞争
模型假设:
- 总人数 N N N 不变。人群分为健康者、病人和病愈免疫的移出者(Removed)三类。其所占比咧分别记为 s ( t ) , i ( t ) , r ( t ) s(t),i(t),r(t) s(t),i(t),r(t)
- 病人的日接触率为 λ \lambda λ ,日治愈率为 μ \mu μ ,传染期接触数 σ = λ μ \sigma=\frac{\lambda}{\mu} σ=μλ
有 s ( t ) + i ( t ) + r ( t ) = 1 s(t)+i(t)+r(t)=1 s(t)+i(t)+r(t)=1 ,但是健康者的比例是持续下降的
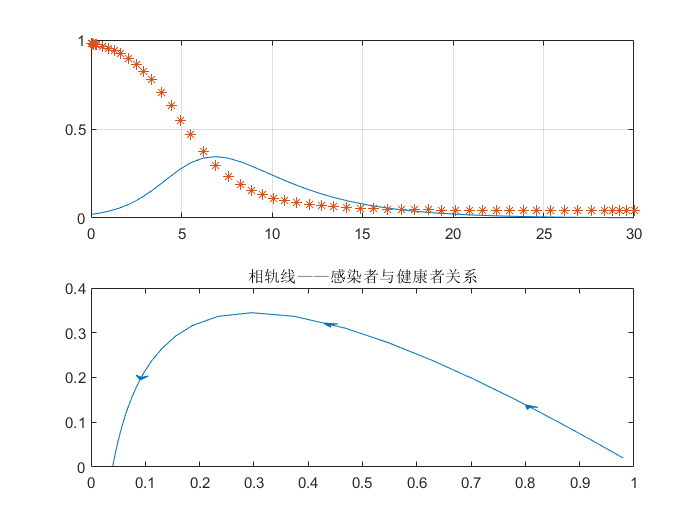
{ d i d t = λ s i − μ i , i ( 0 ) = i 0 d s d t = − λ s i , s ( 0 ) = s 0 \left\{ \begin{array}{l} \frac{di}{dt} = \lambda si - \mu i,\;i(0) = {i_0}\\ \frac{ds}{dt} = - \lambda si,\;s(0) = {s_0} \end{array} \right. {dtdi=λsi−μi,i(0)=i0dtds=−λsi,s(0)=s0
取定固定参数便可以绘制出两个比例的数值解
但是仅仅了解此还不能分析出一般的规律,需要进行相轨线分析
相轨线的定义域只有像平面的左下半边: s ≥ 0 , t ≥ 0 , s + t ≤ 1 s\ge0,t\ge0,s+t \le 1 s≥0,t≥0,s+t≤1
相轨线分析
由微分方程组还可以得出 i , s i,s i,s 之间关系,从而
i = ( i 0 + s 0 ) − s + 1 σ ln s s 0 i=(i_0+s_0)-s+\frac{1}{\sigma}\ln \frac{s}{s_0} i=(i0+s0)−s+σ1lns0s
进而可以进行相关的分析。令 i = 0 i=0 i=0 可以得出最后还剩的健康者比例
s 0 + i 0 − s ∞ + 1 σ ln s ∞ s 0 = 0 s_0+i_0-s_{\infty}+\frac{1}{\sigma}\ln \frac{s_{\infty}}{s_0}=0 s0+i0−s∞+σ1lns0s∞=0
这个式子的意义还在与估计 σ \sigma σ ,事实上其他两个参数并不好估计,而计算接触数只需传染的起点和终点数据
具体详尽分析略,重点在于绘制出美观的相轨线分析图
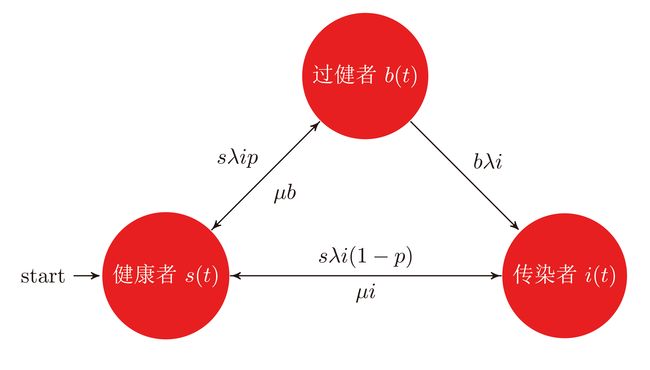
SIB 模型(自建)
部分生活中的模型在健康与感染中其实存在这一个过渡状态或者混合状态,故而修正为以下模型:
此图用 LaTeX \LaTeX LATEX 绘制,过键改为过渡
模型假设:
- 系统总人数 N N N 保持不变,并存在三种状态且 s ( t ) + i ( t ) + b ( t ) = 1 s(t)+i(t)+b(t)=1 s(t)+i(t)+b(t)=1 。其中过渡者没有感染他人的能力,有可能继续被感染为传染者,也有可能被治愈好返回健康者阵营
- 健康者在收到感染时以概率 p p p 转移为过渡者,概率 1 − p 1-p 1−p 转移为传染者
事实上若要考虑死亡只需要切断转移回健康者的两种途径
{ d i d t = λ s i ( 1 − p ) + λ s b − μ i , i ( 0 ) = i 0 d s d t = μ ( i + b ) − λ s i , s ( 0 ) = s 0 d b d t = λ s i p − λ i b − μ b , b ( 0 ) = b 0 \left\{ \begin{array}{l} \frac{di}{dt} = \lambda si(1 - p) + \lambda sb - \mu i,\;i(0) = {i_0}\\ \frac{ds}{dt}= \mu (i + b) - \lambda si,\;s(0) = {s_0}\\ \frac{db}{dt} = \lambda sip - \lambda ib - \mu b,\;b(0) = {b_0} \end{array} \right. ⎩⎨⎧dtdi=λsi(1−p)+λsb−μi,i(0)=i0dtds=μ(i+b)−λsi,s(0)=s0dtdb=λsip−λib−μb,b(0)=b0
事实上可能过渡者的加入对模型影响并不大,但是针对实际情况可能有考虑的必要,你们帮忙检查下有没有问题
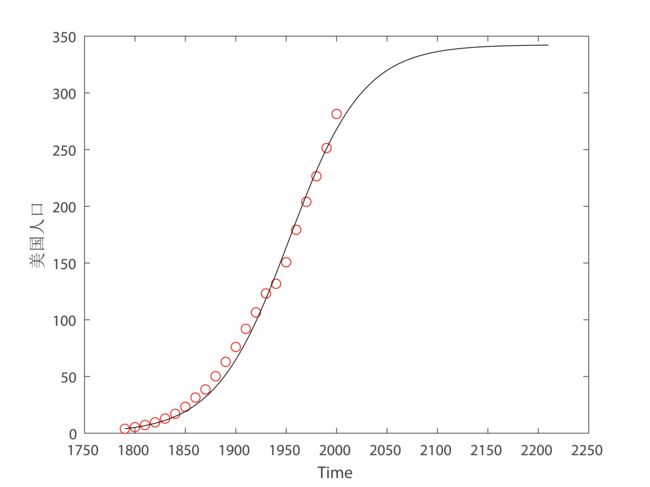
人口阻滞增长模型 Logistic
以美国人口的预测模型为例,小黄书112页
{ d x d t = r ( 1 − x x m ) x x ( t 0 ) = x 0 \left\{ \begin{array}{l} \frac{dx}{dt} = r(1 - \frac{x}{x_m})x\\ x(t_0) = x_0 \end{array} \right. {dtdx=r(1−xmx)xx(t0)=x0
从而
x ( t ) = x m 1 + ( x m x 0 − 1 ) e − r ( t − t 0 ) x(t)=\frac{x_m}{1+(\frac{x_m}{x_0}-1)e^{-r(t-t_0)}} x(t)=1+(x0xm−1)e−r(t−t0)xm
估计参数 r , x m r,x_m r,xm,结果如下
但却是不同的方法估计的参数会有些许不同, r = b e t a ( 1 ) , x m = b e t a ( 2 ) r=beta(1),x_m=beta(2) r=beta(1),xm=beta(2)
beta =
0.0274 342.4351Estimated Parameters by Lsqnonlin():
beta 1 = 0.0274 ± 0.0009
beta 2 = 342.4351 ± 31.3952
The sum of the residual squares is: 1.2e+03
下面对比以下用时间序列处理会得到什么结果
可见时间序列并不会反映出模型系统机理,仅仅是从数据出发并且预测的越远误差越大,除非数据本身规律性很强(周期性等),此处的ARIMA自动预测采取了二阶差分,因为一般时间序列无法解释指数型模型
正规战和游击战
Lanchester 提出的模型是十分简单的,而且仅仅考虑了双方兵力的影响而忽视了政治、经济、社会等因素。因此用这些模型来预测整个战争的结局几乎不可能,但是对于局部战争或许还有参考价值。最为关键的是他为我们其他地方的系统建模提供了一个思路。
一般战争模型
用 x ( t ) , y ( t ) x(t),y(t) x(t),y(t) 分别表示甲乙交战双方时刻 t t t 的兵力,不妨视为双方的士兵人数。假设:
- 每一方的战斗减员取决于双方的战斗力和兵力,甲乙双方的战斗减员率分别用 f ( x , y ) , g ( x , y ) f(x,y),g(x,y) f(x,y),g(x,y) 来表示
- 每一方的非战斗减员率仅与本方的兵力成正比
- 甲乙双方的增援率是给定的函数
{ d x d t = − f ( x , y ) − α x + u ( t ) d y d x = − g ( x , y ) − β y + v ( t ) \left\{ \begin{array}{l} \frac{dx}{dt} = - f(x,y) - \alpha x + u(t)\\ \frac{dy}{dx}= - g(x,y) - \beta y + v(t) \end{array} \right. {dtdx=−f(x,y)−αx+u(t)dxdy=−g(x,y)−βy+v(t)
正规战争
甲乙双方都用正规军作战,简化模型自身战斗减员率只与对方兵力有关,且不考虑非战争因素与援兵,则 f ( x , y ) = a y , g ( x , y ) = b x , α = β = u = v = 0 f(x,y)=ay,g(x,y)=b x,\alpha=\beta=u=v=0 f(x,y)=ay,g(x,y)=bx,α=β=u=v=0 。
从而
d y d x = b x a y \frac{dy}{dx}=\frac{bx}{ay} dxdy=aybx
故 a y 2 − b x 2 = k ay^2-bx^2=k ay2−bx2=k 。分析相轨线可知这是一簇双曲线, k = 0 k=0 k=0 为平局。从而乙方获胜的条件是
( y 0 x 0 ) 2 > b a (\frac{y_0}{x_0})^2>\frac{b}{a} (x0y0)2>ab
由于这个原因,正规战也被称为是平方律模型 。
游击战模型
与正规战争区别在于考虑了活动面积,模型称为:
f ( x , y ) = c x y , g ( x , y ) = d x y , α = β = u = v = 0 f(x,y)=cxy,g(x,y)=dxy ,\alpha=\beta=u=v=0 f(x,y)=cxy,g(x,y)=dxy,α=β=u=v=0
相轨线为 c y − d x = m cy-dx=m cy−dx=m ,是一簇直线,从而这个模型又被称为线性律模型。
混合战役——游击VS正规
此时正规军一般至少要输出数倍与游击军的兵力方能取胜。
按年龄分组的种群增长模型(Leslie)
下面提到的是雌性数量,整体数量可以用一定性别比得出。计时间段 k k k 第 i i i 年龄组的的种群数量为 x i ( k ) , k = 0 , 1 , 2 , ⋯ , i = 1 , 2 , ⋯ , n x_i(k),k=0,1,2,\cdots,i=1,2,\cdots,n xi(k),k=0,1,2,⋯,i=1,2,⋯,n 。并合理的假设繁殖率和死亡率只与年龄组有关,与时间段无关。计第 i i i 年龄组的繁殖率为 b i b_i bi (一个时段内繁殖的数量);计第 i i i 年龄组的死亡率为 d i d_i di (一个时段内死亡数量的比例);
是不是繁殖的和死亡也只计算雌性的?
易得关系:
x 1 ( k + 1 ) = ∑ i = 1 n b i x i ( k ) , k = 0 , 1 , 2 , ⋯ x i + 1 ( k + 1 ) = s i x i ( k ) , k = 0 , 1 , 2 ⋯ , i = 1 , 2 , ⋯ , n − 1 \begin{array}{l} x_1(k + 1) = \sum\limits_{i = 1}^n b_i{x_i}(k),\;k = 0,1,2, \cdots \\ x_{i + 1}(k + 1) = s_i{x_i}(k),\;k = 0,1,2 \cdots ,i = 1,2, \cdots ,n - 1 \end{array} x1(k+1)=i=1∑nbixi(k),k=0,1,2,⋯xi+1(k+1)=sixi(k),k=0,1,2⋯,i=1,2,⋯,n−1
由繁殖率与死亡率构成的矩阵
KaTeX parse error: Unknown column alignment: * at position 24: …{\begin{array}{*̲{20}{c}} b_1&b_…
称为 L L L 矩阵,这样递推关系可简写为
x ( k + 1 ) = L ⋅ x ( k ) \boldsymbol{x}(k+1)=\boldsymbol{L}\cdot\boldsymbol{x}(k) x(k+1)=L⋅x(k)
虽然动态过程的变化规律一般要用微分方程建立的动态模型来描述,但是对于某些实际问题,建模的主要目的并不是要寻求动态过程每个瞬时的性态,而是研究某种意义下稳定状态的特征,特别是当时间充分长以后动态过程的变化趋势。
下面先以一个例子讨论差分的稳定性分析,最后给出微分方程与差分方程的稳定性理论
差分形式的阻滞增长模型
将 logistic 模型中的微分用差分改写
y k + 1 − y k = r y k ( 1 − y k N ) , k = 0 , 1 , 2 , ⋯ y_{k+1}-y_k=ry_k(1-\frac{y_k}{N}),k=0,1,2,\cdots yk+1−yk=ryk(1−Nyk),k=0,1,2,⋯
做变量替换 b = r + 1 , x k = r y k / ( r + 1 ) N b=r+1,x_k=ry_k/(r+1)N b=r+1,xk=ryk/(r+1)N ,则上式可简化为
(1) x k + 1 = b x k ( 1 − x k ) x_{k+1}=bx_k(1-x_k) \tag{1} xk+1=bxk(1−xk)(1)
这是一个非线性一阶差分方程。由不动点理论,平衡解为以下方程组得解:
x = f ( x ) = b x ( 1 − x ) x=f(x)=bx(1-x) x=f(x)=bx(1−x)
从而 x ∗ = 1 − 1 / b x^*=1-1/b x∗=1−1/b 。其稳定条件为
∣ f ′ ( x ∗ ) ∣ = b ( 1 − 2 x ∗ ) = 2 − b < 1 |f^{'}(x^*)|=b(1-2x^*)=2-b<1 ∣f′(x∗)∣=b(1−2x∗)=2−b<1
从而 1 < b < 3 1<b<3 1<b<3 。
要学会绘制不动点稳定性的图解法
微分方程稳定性理论简介
定义:称一个常微分方程(组)是自治的,如果方程(组)
d x d t = F ( x , t ) = [ f 1 ( x , t ) ⋮ f 2 ( x , t ) ] \frac{dx}{dt} = F(x,t) = \left[ \begin{array}{l} {f_1}(x,t)\\ \;\;\;\;\; \vdots \\ {f_2}(x,t) \end{array} \right] dtdx=F(x,t)=⎣⎢⎡f1(x,t)⋮f2(x,t)⎦⎥⎤
中的 F ( x , t ) = F ( x ) F(x,t)=F(x) F(x,t)=F(x) ,即在 F F F 中不显含 t t t。
- 相空间中满足 F ( x 0 ) = 0 F(x_0)=0 F(x0)=0 的点 x 0 x_0 x0 称为系统的奇点(或平衡点)。奇点可以是孤立的,也可以是连续的点集。
- 定理:设 F ( x ) F(x) F(x) 是实解析函数,且 x 0 x_0 x0 是系统的奇点。若 F ( x ) F(x) F(x) 在点 x 0 x_0 x0 处的 J a c o b i a n Jacobian Jacobian 矩阵是非奇异的,则 x 0 x_0 x0 是该系统的孤立奇点
- 所有轨线在相空间中的分布图称为相图
- 如果当系统的初始状态靠近于奇点,其轨线对所有的时间 t t t仍然接近它,于是说 x 0 x_0 x0 是稳定的。另一方面,如果当 t → ∞ t\rightarrow \infty t→∞ 时这些轨线趋于 x 0 x_0 x0 ,则 x 0 x_0 x0 是渐近稳定的
- 常系数齐次线性系统的零解是渐进稳定的的充分必要条件是 A A A 的一切特征根的实部全部都是负的
- 对于非线性系统,一般不可能找出其积分曲线或轨迹,也就不可能直接导出奇点的稳定性。为克服这一困难,在奇点附近用一个线性系统来近似这个非线性系统,用这个近似系统的解来给出这个奇点的稳定解
一阶微分方程
利用定义成为间接法,本初可以利用直接法而不利用下述定义:
零点稳定性定义:
如果对任意给定的 ϵ > 0 \epsilon >0 ϵ>0 ,存在 δ > 0 \delta>0 δ>0 ,使得对任意的 x 0 x_0 x0 满足 ∣ ∣ x 0 ∣ ∣ ≤ δ ||x_0|| \le \delta ∣∣x0∣∣≤δ 时,方程组由初值 x ( t o ) = x 0 x(t_o)=x_0 x(to)=x0 确定的解 x ( t ) x(t) x(t) ,对一切的 t ≥ t 0 t \ge t_0 t≥t0 均有
∣ ∣ x ( t ) ∣ ∣ ≤ ϵ ||x(t)||\le \epsilon ∣∣x(t)∣∣≤ϵ
将 f ( x ) f(x) f(x) 在 x 0 x_0 x0 处展开,只取一次项,方程 d x d t = f ( x ) \frac{dx}{dt}=f(x) dtdx=f(x) 近似为
d x d t = f ′ ( x 0 ) ( x − x 0 ) \frac{dx}{dt}=f^{'}(x_0)(x-x_0) dtdx=f′(x0)(x−x0)
- 若 f ′ ( x 0 ) < 0 f^{'}(x_0)<0 f′(x0)<0 ,则 x 0 x_0 x0 稳定
- 若 f ′ ( x 0 ) > 0 f^{'}(x_0)>0 f′(x0)>0 ,则不稳定
二阶方程的平衡点与稳定性
参见数模选修作业,文件位于项目: \数学原理\
简单来说遇到非线性的线性化,然后求特征方程看系数:
λ 2 + p λ + q = 0 \lambda^2+p\lambda+q=0 λ2+pλ+q=0
p > 0 , q > 0 p>0,q>0 p>0,q>0 则平衡点稳定。
n n n 阶是否可以推广待续
差分方程平衡点的稳定性
此时平衡点的关键定义变为 x k + 1 = x k x_{k+1}=x_k xk+1=xk
不动点理论
一阶差分
x k + 1 + a x k = 0 → x k = ( − a ) k x 0 x_{k+1}+ax_k=0 \rightarrow x_k=(-a)^kx_0 xk+1+axk=0→xk=(−a)kx0 ,从而必须 ∣ a ∣ < 1 |a|<1 ∣a∣<1 。推广如下
对于 n n n 维向量 x ( k ) \boldsymbol{x}(k) x(k) 和常数矩阵 A \boldsymbol{A} A 构成的方程组
x ( k + 1 ) + A x ( k ) = 0 \boldsymbol{x}(k+1)+\boldsymbol{A}\boldsymbol{x}(k)=0 x(k+1)+Ax(k)=0
其平衡点稳定的条件是 A \boldsymbol{A} A 的特征值的绝对值全部小于1。 ∣ λ i ∣ < 1 , i = 1 , 2 , ⋯ , n |\lambda_i |<1,i=1,2,\cdots,n ∣λi∣<1,i=1,2,⋯,n
n n n 阶线性差分方程
同样是特征方程—— n n n 次代数方程的跟绝对值小于1
一阶非线性差分
同样线性化,
x k + 1 = f ′ ( x ∗ ) ( x k − x ∗ ) + f ( x ∗ ) x_{k+1}=f^{'}(x^*)(x_k-x^*)+f(x^*) xk+1=f′(x∗)(xk−x∗)+f(x∗)
当 ∣ f ′ ( x ∗ ) ∣ ≠ 1 |f^{'}(x^*)| \ne1 ∣f′(x∗)∤=1 时,线性化前后稳定性一致。